Designing Machine Learning Toolboxes: Concepts, Principles and Patterns

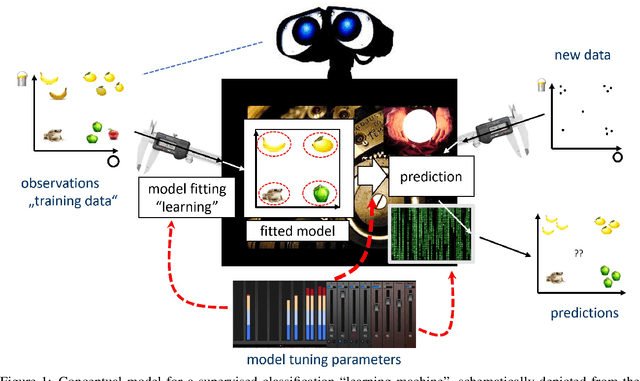
Machine learning (ML) and AI toolboxes such as scikit-learn or Weka are workhorses of contemporary data scientific practice -- their central role being enabled by usable yet powerful designs that allow to easily specify, train and validate complex modeling pipelines. However, despite their universal success, the key design principles in their construction have never been fully analyzed. In this paper, we attempt to provide an overview of key patterns in the design of AI modeling toolboxes, taking inspiration, in equal parts, from the field of software engineering, implementation patterns found in contemporary toolboxes, and our own experience from developing ML toolboxes. In particular, we develop a conceptual model for the AI/ML domain, with a new type system, called scientific types, at its core. Scientific types capture the scientific meaning of common elements in ML workflows based on the set of operations that we usually perform with them (i.e. their interface) and their statistical properties. From our conceptual analysis, we derive a set of design principles and patterns. We illustrate that our analysis can not only explain the design of existing toolboxes, but also guide the development of new ones. We intend our contribution to be a state-of-art reference for future toolbox engineers, a summary of best practices, a collection of ML design patterns which may become useful for future research, and, potentially, the first steps towards a higher-level programming paradigm for constructing AI.

Kernels for time series with irregularly-spaced multivariate observations

Time series are an interesting frontier for kernel-based methods, for the simple reason that there is no kernel designed to represent them and their unique characteristics in full generality. Existing sequential kernels ignore the time indices, with many assuming that the series must be regularly-spaced; some such kernels are not even psd. In this manuscript, we show that a "series kernel" that is general enough to represent irregularly-spaced multivariate time series may be built out of well-known "vector kernels". We also show that all series kernels constructed using our methodology are psd, and are thus widely applicable. We demonstrate this point by formulating a Gaussian process-based strategy - with our series kernel at its heart - to make predictions about test series when given a training set. We validate the strategy experimentally by estimating its generalisation error on multiple datasets and comparing it to relevant baselines. We also demonstrate that our series kernel may be used for the more traditional setting of time series classification, where its performance is broadly in line with alternative methods.