The Algebraic Combinatorial Approach for Low-Rank Matrix Completion

We present a novel algebraic combinatorial view on low-rank matrix completion based on studying relations between a few entries with tools from algebraic geometry and matroid theory. The intrinsic locality of the approach allows for the treatment of single entries in a closed theoretical and practical framework. More specifically, apart from introducing an algebraic combinatorial theory of low-rank matrix completion, we present probability-one algorithms to decide whether a particular entry of the matrix can be completed. We also describe methods to complete that entry from a few others, and to estimate the error which is incurred by any method completing that entry. Furthermore, we show how known results on matrix completion and their sampling assumptions can be related to our new perspective and interpreted in terms of a completability phase transition.

Algebraic-Combinatorial Methods for Low-Rank Matrix Completion with Application to Athletic Performance Prediction

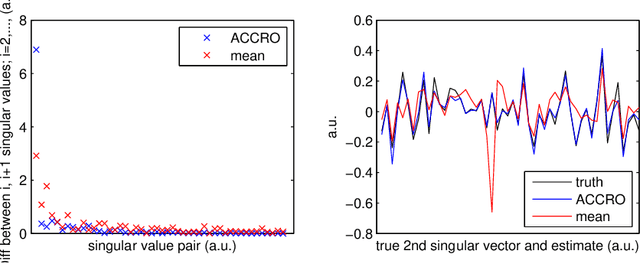
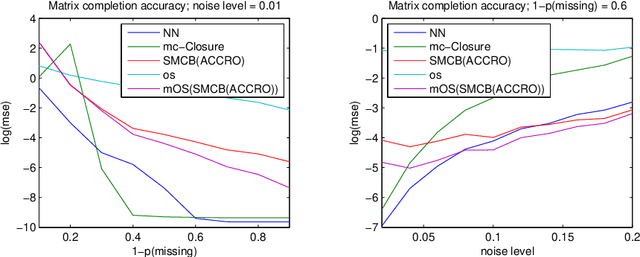
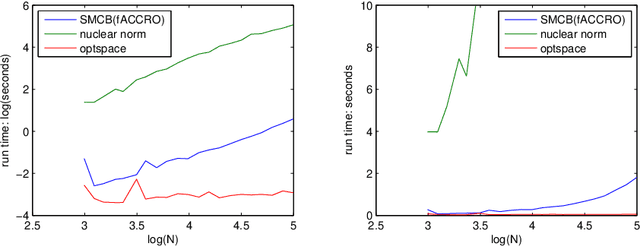
This paper presents novel algorithms which exploit the intrinsic algebraic and combinatorial structure of the matrix completion task for estimating missing en- tries in the general low rank setting. For positive data, we achieve results out- performing the state of the art nuclear norm, both in accuracy and computational efficiency, in simulations and in the task of predicting athletic performance from partially observed data.

Learning with Cross-Kernels and Ideal PCA

We describe how cross-kernel matrices, that is, kernel matrices between the data and a custom chosen set of `feature spanning points' can be used for learning. The main potential of cross-kernels lies in the fact that (a) only one side of the matrix scales with the number of data points, and (b) cross-kernels, as opposed to the usual kernel matrices, can be used to certify for the data manifold. Our theoretical framework, which is based on a duality involving the feature space and vanishing ideals, indicates that cross-kernels have the potential to be used for any kind of kernel learning. We present a novel algorithm, Ideal PCA (IPCA), which cross-kernelizes PCA. We demonstrate on real and synthetic data that IPCA allows to (a) obtain PCA-like features faster and (b) to extract novel and empirically validated features certifying for the data manifold.

Matroid Regression

We propose an algebraic combinatorial method for solving large sparse linear systems of equations locally - that is, a method which can compute single evaluations of the signal without computing the whole signal. The method scales only in the sparsity of the system and not in its size, and allows to provide error estimates for any solution method. At the heart of our approach is the so-called regression matroid, a combinatorial object associated to sparsity patterns, which allows to replace inversion of the large matrix with the inversion of a kernel matrix that is constant size. We show that our method provides the best linear unbiased estimator (BLUE) for this setting and the minimum variance unbiased estimator (MVUE) under Gaussian noise assumptions, and furthermore we show that the size of the kernel matrix which is to be inverted can be traded off with accuracy.

Dual-to-kernel learning with ideals

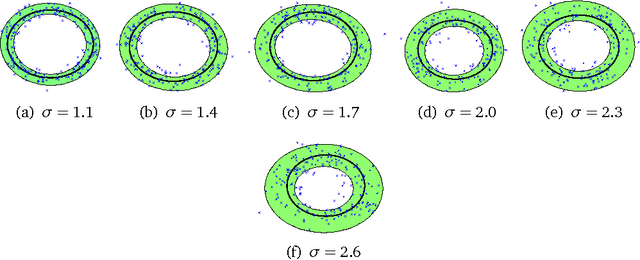
In this paper, we propose a theory which unifies kernel learning and symbolic algebraic methods. We show that both worlds are inherently dual to each other, and we use this duality to combine the structure-awareness of algebraic methods with the efficiency and generality of kernels. The main idea lies in relating polynomial rings to feature space, and ideals to manifolds, then exploiting this generative-discriminative duality on kernel matrices. We illustrate this by proposing two algorithms, IPCA and AVICA, for simultaneous manifold and feature learning, and test their accuracy on synthetic and real world data.

Coherence and sufficient sampling densities for reconstruction in compressed sensing

We give a new, very general, formulation of the compressed sensing problem in terms of coordinate projections of an analytic variety, and derive sufficient sampling rates for signal reconstruction. Our bounds are linear in the coherence of the signal space, a geometric parameter independent of the specific signal and measurement, and logarithmic in the ambient dimension where the signal is presented. We exemplify our approach by deriving sufficient sampling densities for low-rank matrix completion and distance matrix completion which are independent of the true matrix.

Obtaining error-minimizing estimates and universal entry-wise error bounds for low-rank matrix completion

We propose a general framework for reconstructing and denoising single entries of incomplete and noisy entries. We describe: effective algorithms for deciding if and entry can be reconstructed and, if so, for reconstructing and denoising it; and a priori bounds on the error of each entry, individually. In the noiseless case our algorithm is exact. For rank-one matrices, the new algorithm is fast, admits a highly-parallel implementation, and produces an error minimizing estimate that is qualitatively close to our theoretical and the state-of-the-are Nuclear Norm and OptSpace methods.