Transferring Subspaces Between Subjects in Brain-Computer Interfacing

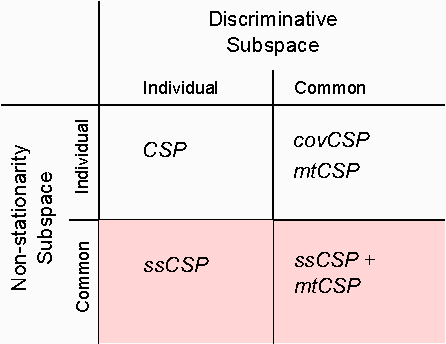
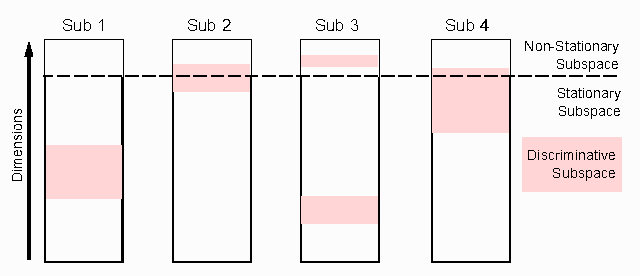
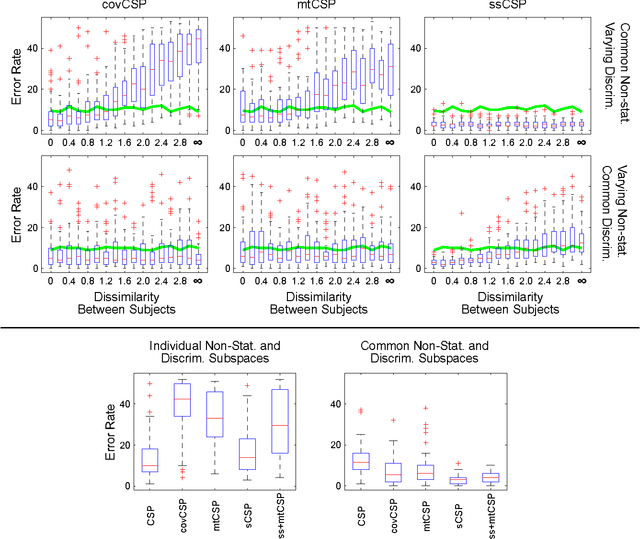
Compensating changes between a subjects' training and testing session in Brain Computer Interfacing (BCI) is challenging but of great importance for a robust BCI operation. We show that such changes are very similar between subjects, thus can be reliably estimated using data from other users and utilized to construct an invariant feature space. This novel approach to learning from other subjects aims to reduce the adverse effects of common non-stationarities, but does not transfer discriminative information. This is an important conceptual difference to standard multi-subject methods that e.g. improve the covariance matrix estimation by shrinking it towards the average of other users or construct a global feature space. These methods do not reduces the shift between training and test data and may produce poor results when subjects have very different signal characteristics. In this paper we compare our approach to two state-of-the-art multi-subject methods on toy data and two data sets of EEG recordings from subjects performing motor imagery. We show that it can not only achieve a significant increase in performance, but also that the extracted change patterns allow for a neurophysiologically meaningful interpretation.

Explorative Data Analysis for Changes in Neural Activity

Neural recordings are nonstationary time series, i.e. their properties typically change over time. Identifying specific changes, e.g. those induced by a learning task, can shed light on the underlying neural processes. However, such changes of interest are often masked by strong unrelated changes, which can be of physiological origin or due to measurement artifacts. We propose a novel algorithm for disentangling such different causes of non-stationarity and in this manner enable better neurophysiological interpretation for a wider set of experimental paradigms. A key ingredient is the repeated application of Stationary Subspace Analysis (SSA) using different temporal scales. The usefulness of our explorative approach is demonstrated in simulations, theory and EEG experiments with 80 Brain-Computer-Interfacing (BCI) subjects.

Algebraic Geometric Comparison of Probability Distributions

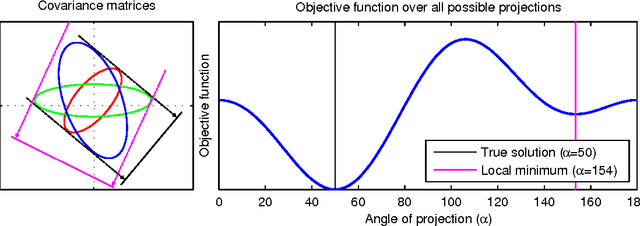
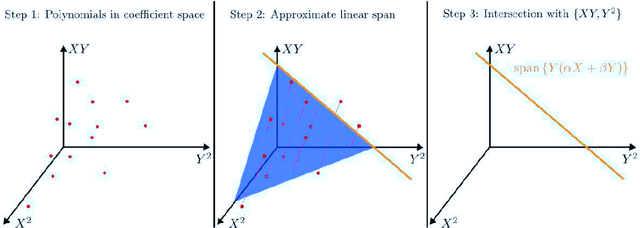
We propose a novel algebraic framework for treating probability distributions represented by their cumulants such as the mean and covariance matrix. As an example, we consider the unsupervised learning problem of finding the subspace on which several probability distributions agree. Instead of minimizing an objective function involving the estimated cumulants, we show that by treating the cumulants as elements of the polynomial ring we can directly solve the problem, at a lower computational cost and with higher accuracy. Moreover, the algebraic viewpoint on probability distributions allows us to invoke the theory of Algebraic Geometry, which we demonstrate in a compact proof for an identifiability criterion.