Orbital-free Bond Breaking via Machine Learning

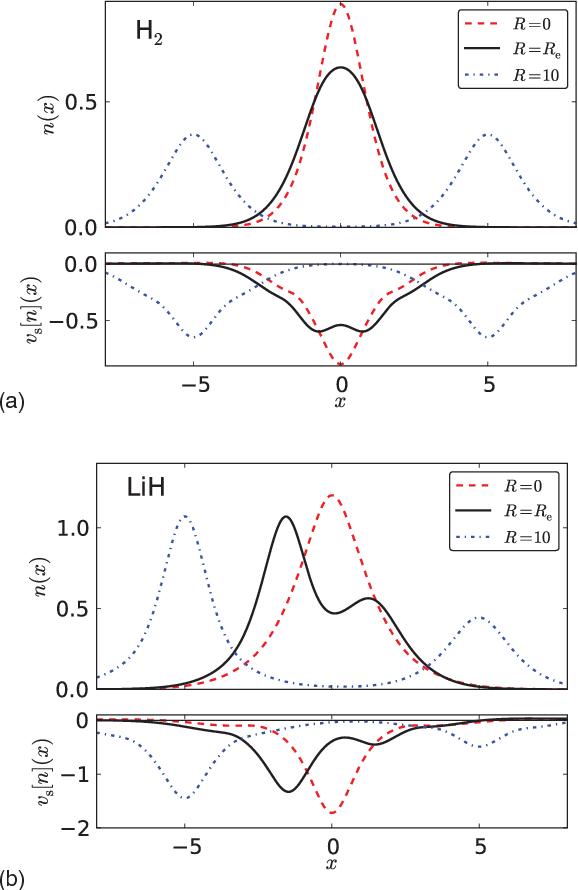
Machine learning is used to approximate the kinetic energy of one dimensional diatomics as a functional of the electron density. The functional can accurately dissociate a diatomic, and can be systematically improved with training. Highly accurate self-consistent densities and molecular forces are found, indicating the possibility for ab-initio molecular dynamics simulations.

Finding Density Functionals with Machine Learning

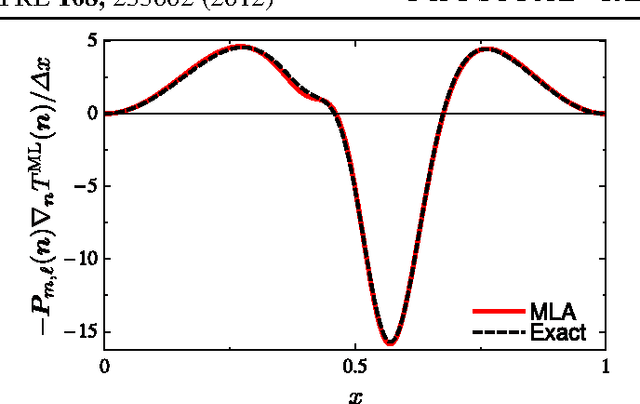
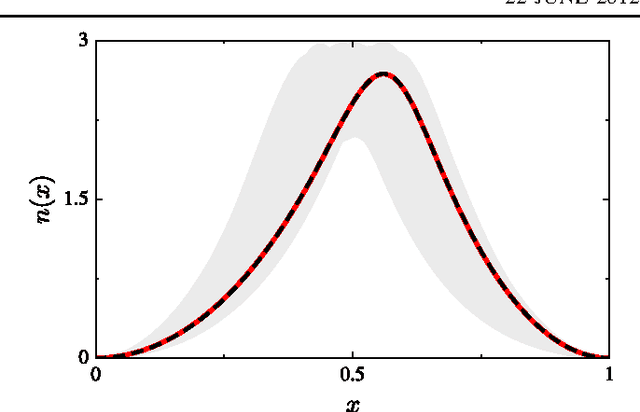
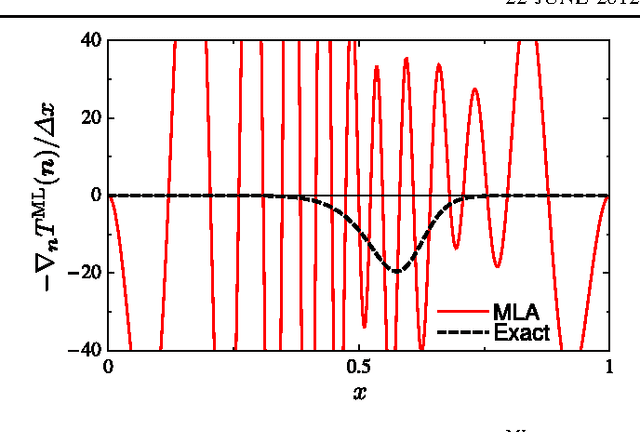
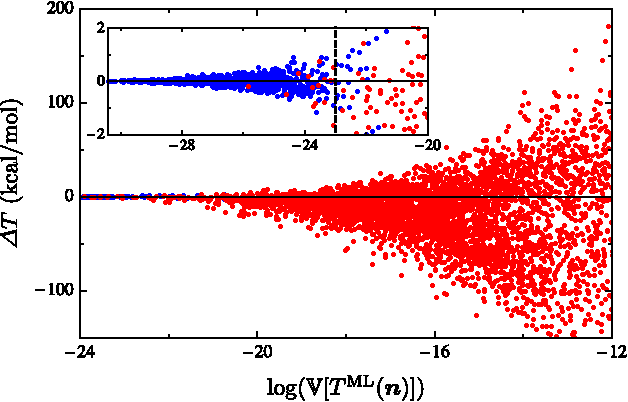
Machine learning is used to approximate density functionals. For the model problem of the kinetic energy of non-interacting fermions in 1d, mean absolute errors below 1 kcal/mol on test densities similar to the training set are reached with fewer than 100 training densities. A predictor identifies if a test density is within the interpolation region. Via principal component analysis, a projected functional derivative finds highly accurate self-consistent densities. Challenges for application of our method to real electronic structure problems are discussed.

How to Explain Individual Classification Decisions

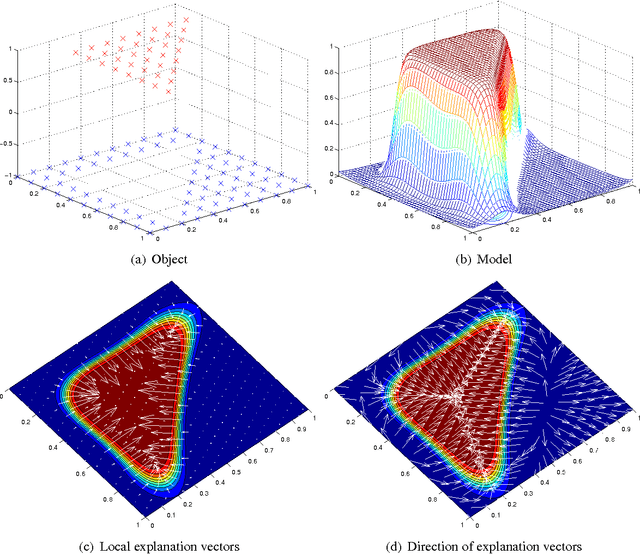
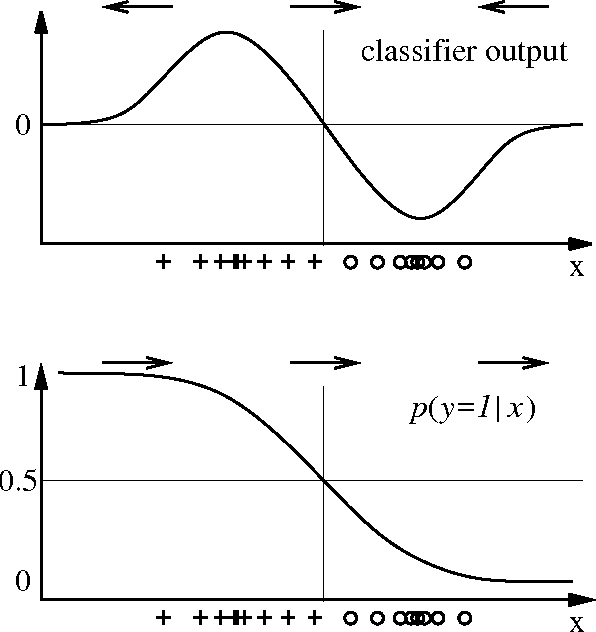
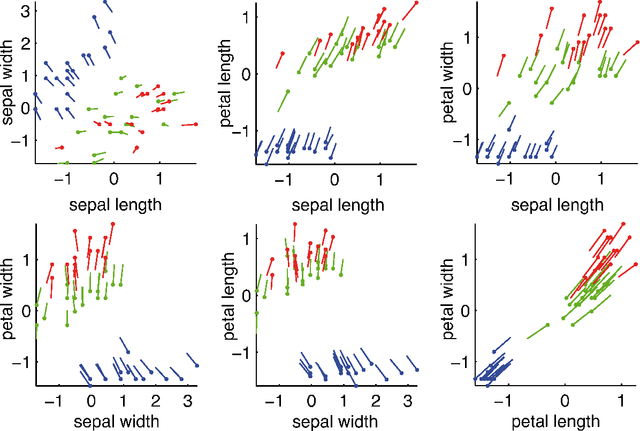
After building a classifier with modern tools of machine learning we typically have a black box at hand that is able to predict well for unseen data. Thus, we get an answer to the question what is the most likely label of a given unseen data point. However, most methods will provide no answer why the model predicted the particular label for a single instance and what features were most influential for that particular instance. The only method that is currently able to provide such explanations are decision trees. This paper proposes a procedure which (based on a set of assumptions) allows to explain the decisions of any classification method.