Matthias Rupp
Code Generation for Machine Learning using Model-Driven Engineering and SysML
Jul 10, 2023Abstract:Data-driven engineering refers to systematic data collection and processing using machine learning to improve engineering systems. Currently, the implementation of data-driven engineering relies on fundamental data science and software engineering skills. At the same time, model-based engineering is gaining relevance for the engineering of complex systems. In previous work, a model-based engineering approach integrating the formalization of machine learning tasks using the general-purpose modeling language SysML is presented. However, formalized machine learning tasks still require the implementation in a specialized programming languages like Python. Therefore, this work aims to facilitate the implementation of data-driven engineering in practice by extending the previous work of formalizing machine learning tasks by integrating model transformation to generate executable code. The method focuses on the modifiability and maintainability of the model transformation so that extensions and changes to the code generation can be integrated without requiring modifications to the code generator. The presented method is evaluated for feasibility in a case study to predict weather forecasts. Based thereon, quality attributes of model transformations are assessed and discussed. Results demonstrate the flexibility and the simplicity of the method reducing efforts for implementation. Further, the work builds a theoretical basis for standardizing data-driven engineering implementation in practice.
Heat flux for semi-local machine-learning potentials
Mar 28, 2023



Abstract:The Green-Kubo (GK) method is a rigorous framework for heat transport simulations in materials. However, it requires an accurate description of the potential-energy surface and carefully converged statistics. Machine-learning potentials can achieve the accuracy of first-principles simulations while allowing to reach well beyond their simulation time and length scales at a fraction of the cost. In this paper, we explain how to apply the GK approach to the recent class of message-passing machine-learning potentials, which iteratively consider semi-local interactions beyond the initial interaction cutoff. We derive an adapted heat flux formulation that can be implemented using automatic differentiation without compromising computational efficiency. The approach is demonstrated and validated by calculating the thermal conductivity of zirconium dioxide across temperatures.
Representations of molecules and materials for interpolation of quantum-mechanical simulations via machine learning
Mar 26, 2020


Abstract:Computational study of molecules and materials from first principles is a cornerstone of physics, chemistry and materials science, but limited by the cost of accurate and precise simulations. In settings involving many simulations, machine learning can reduce these costs, sometimes by orders of magnitude, by interpolating between reference simulations. This requires representations that describe any molecule or material and support interpolation. We review, discuss and benchmark state-of-the-art representations and relations between them, including smooth overlap of atomic positions, many-body tensor representation, and symmetry functions. For this, we use a unified mathematical framework based on many-body functions, group averaging and tensor products, and compare energy predictions for organic molecules, binary alloys and Al-Ga-In sesquioxides in numerical experiments controlled for data distribution, regression method and hyper-parameter optimization.
Assessing the Frontier: Active Learning, Model Accuracy, and Multi-objective Materials Discovery and Optimization
Nov 06, 2019

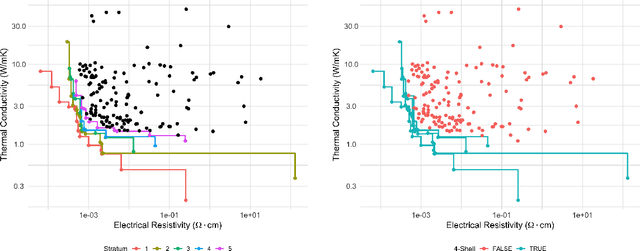
Abstract:Discovering novel materials can be greatly accelerated by iterative machine learning-informed proposal of candidates---active learning. However, standard \emph{global-scope error} metrics for model quality are not predictive of discovery performance, and can be misleading. We introduce the notion of \emph{Pareto shell-scope error} to help judge the suitability of a model for proposing material candidates. Further, through synthetic cases and a thermoelectric dataset, we probe the relation between acquisition function fidelity and active learning performance. Results suggest novel diagnostic tools, as well as new insights for acquisition function design.
Understanding Kernel Ridge Regression: Common behaviors from simple functions to density functionals
Jan 28, 2015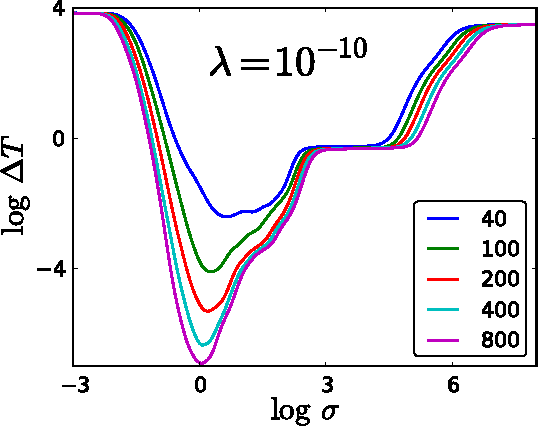

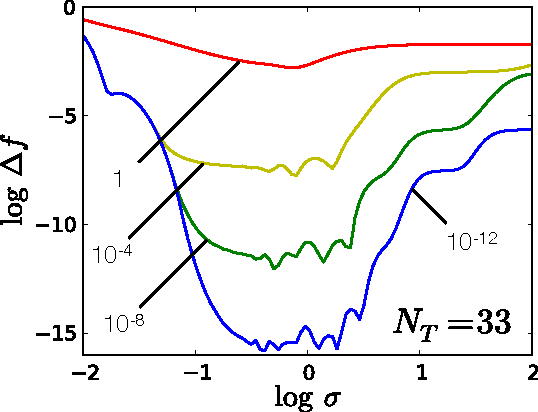
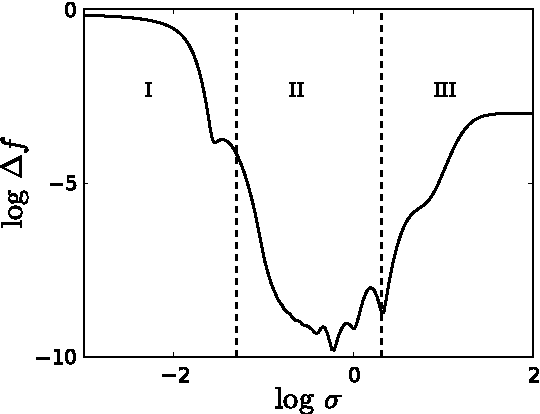
Abstract:Accurate approximations to density functionals have recently been obtained via machine learning (ML). By applying ML to a simple function of one variable without any random sampling, we extract the qualitative dependence of errors on hyperparameters. We find universal features of the behavior in extreme limits, including both very small and very large length scales, and the noise-free limit. We show how such features arise in ML models of density functionals.
Understanding Machine-learned Density Functionals
May 27, 2014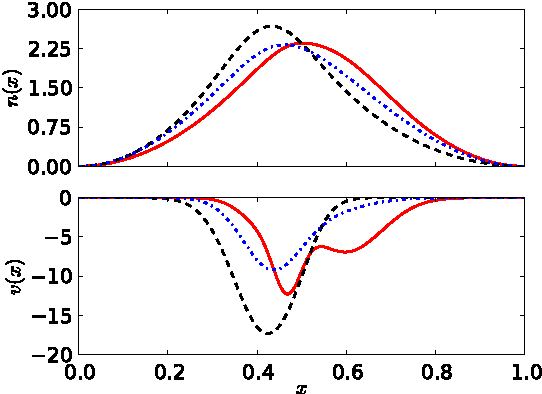
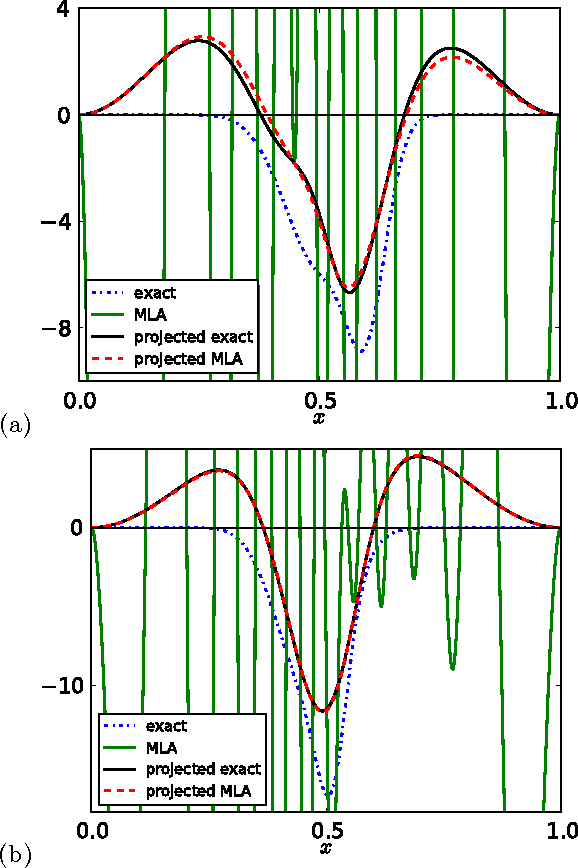
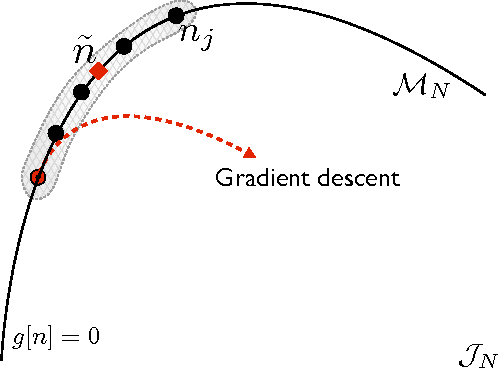
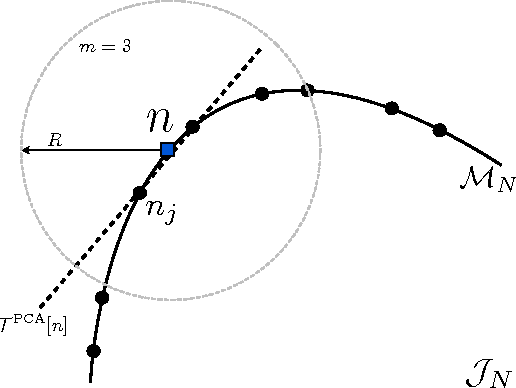
Abstract:Kernel ridge regression is used to approximate the kinetic energy of non-interacting fermions in a one-dimensional box as a functional of their density. The properties of different kernels and methods of cross-validation are explored, and highly accurate energies are achieved. Accurate {\em constrained optimal densities} are found via a modified Euler-Lagrange constrained minimization of the total energy. A projected gradient descent algorithm is derived using local principal component analysis. Additionally, a sparse grid representation of the density can be used without degrading the performance of the methods. The implications for machine-learned density functional approximations are discussed.
Orbital-free Bond Breaking via Machine Learning
Jun 07, 2013
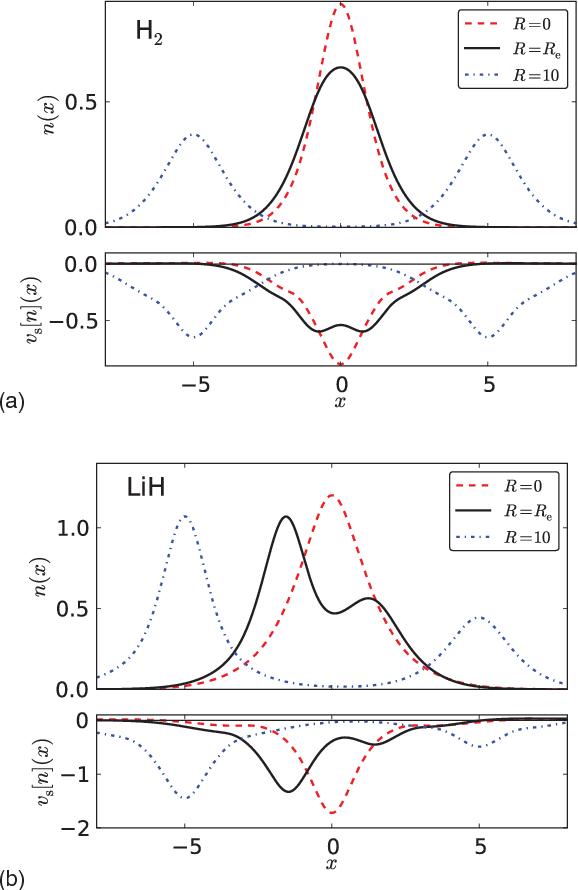

Abstract:Machine learning is used to approximate the kinetic energy of one dimensional diatomics as a functional of the electron density. The functional can accurately dissociate a diatomic, and can be systematically improved with training. Highly accurate self-consistent densities and molecular forces are found, indicating the possibility for ab-initio molecular dynamics simulations.
Finding Density Functionals with Machine Learning
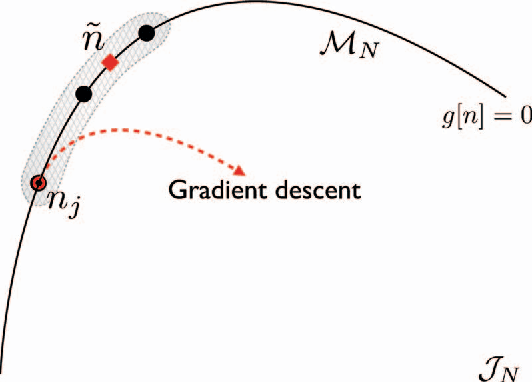
Dec 22, 2011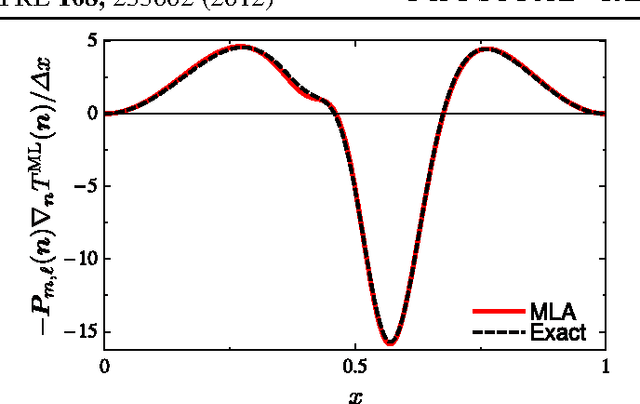
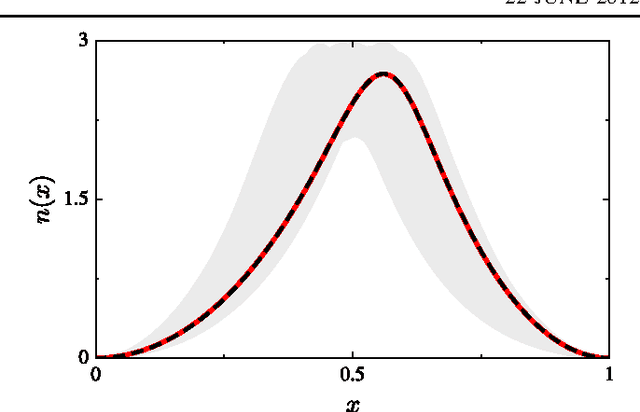
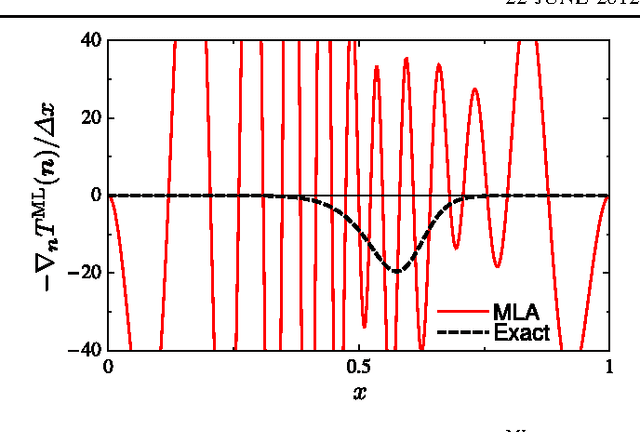
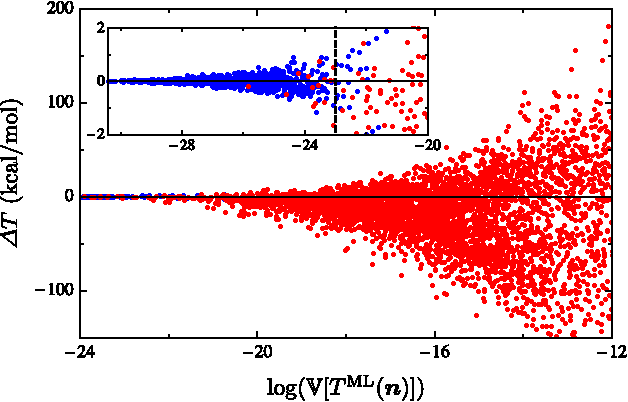
Abstract:Machine learning is used to approximate density functionals. For the model problem of the kinetic energy of non-interacting fermions in 1d, mean absolute errors below 1 kcal/mol on test densities similar to the training set are reached with fewer than 100 training densities. A predictor identifies if a test density is within the interpolation region. Via principal component analysis, a projected functional derivative finds highly accurate self-consistent densities. Challenges for application of our method to real electronic structure problems are discussed.
Fast and Accurate Modeling of Molecular Atomization Energies with Machine Learning
Sep 12, 2011
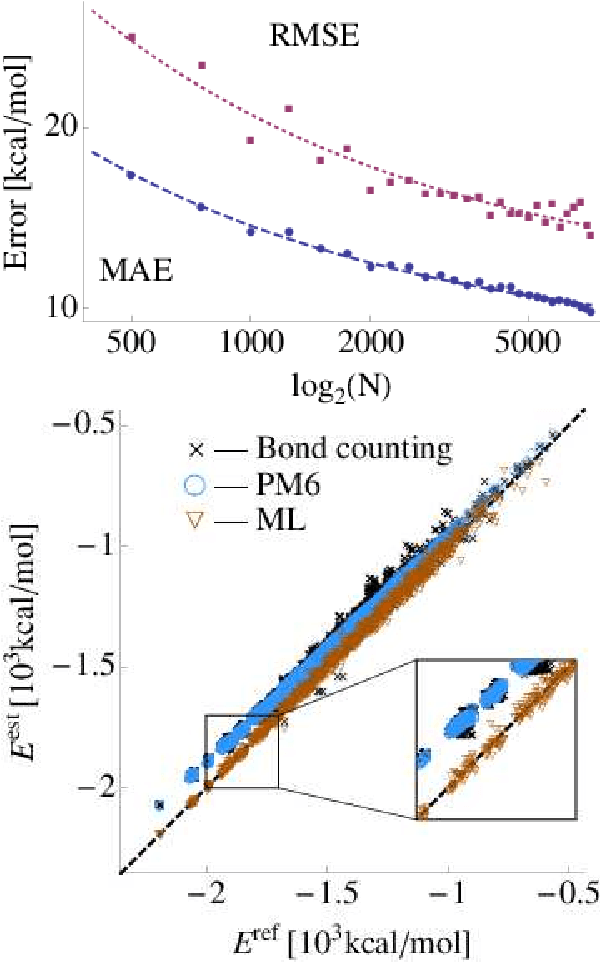
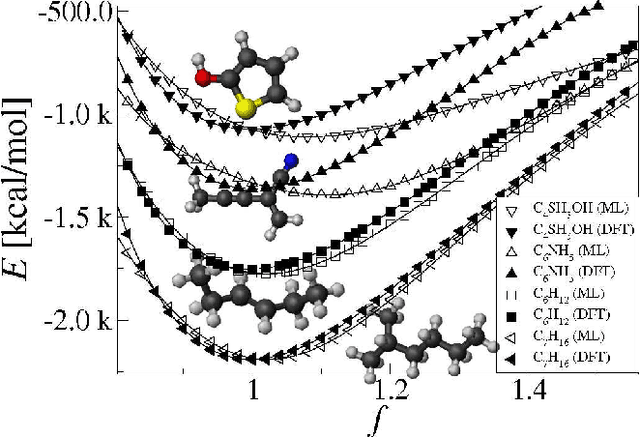
Abstract:We introduce a machine learning model to predict atomization energies of a diverse set of organic molecules, based on nuclear charges and atomic positions only. The problem of solving the molecular Schr\"odinger equation is mapped onto a non-linear statistical regression problem of reduced complexity. Regression models are trained on and compared to atomization energies computed with hybrid density-functional theory. Cross-validation over more than seven thousand small organic molecules yields a mean absolute error of ~10 kcal/mol. Applicability is demonstrated for the prediction of molecular atomization potential energy curves.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge