Data-Error Scaling in Machine Learning on Natural Discrete Combinatorial Mutation-prone Sets: Case Studies on Peptides and Small Molecules

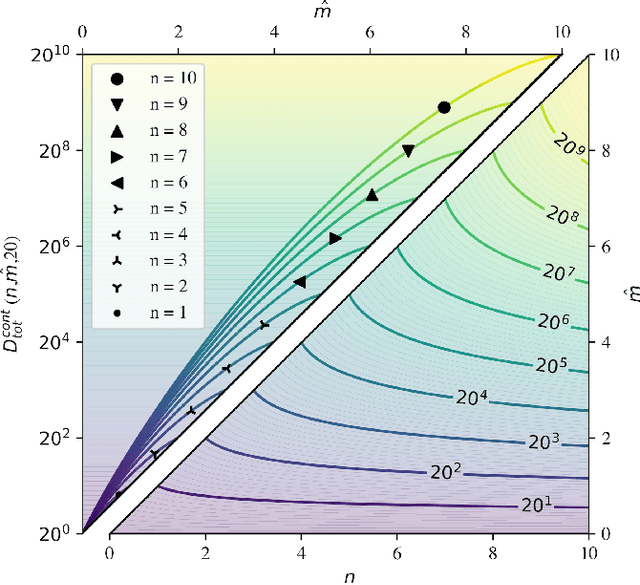
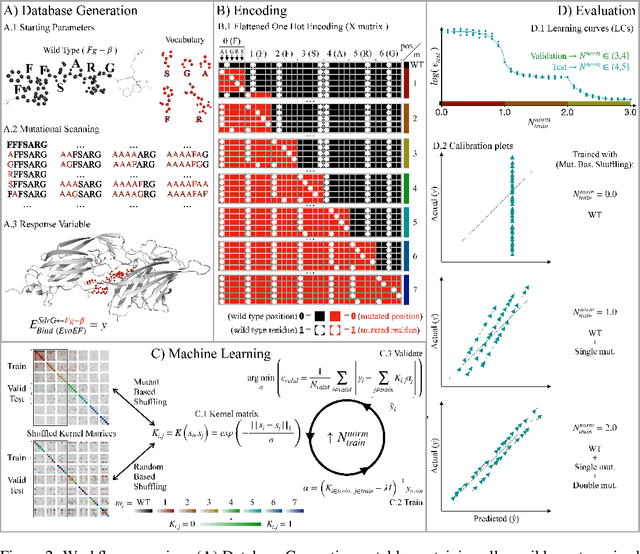
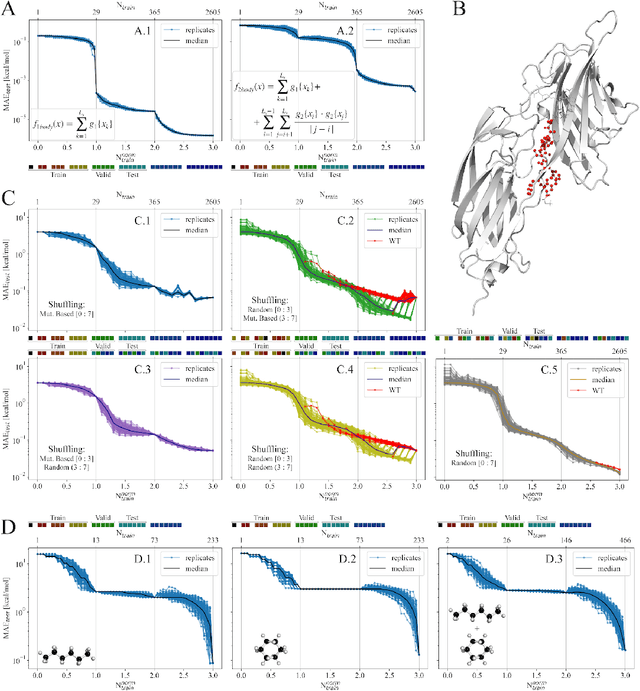
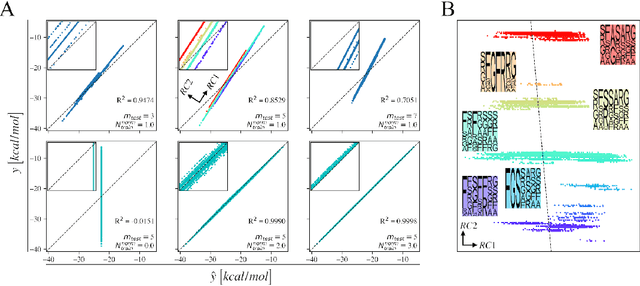
We investigate trends in the data-error scaling behavior of machine learning (ML) models trained on discrete combinatorial spaces that are prone-to-mutation, such as proteins or organic small molecules. We trained and evaluated kernel ridge regression machines using variable amounts of computationally generated training data. Our synthetic datasets comprise i) two na\"ive functions based on many-body theory; ii) binding energy estimates between a protein and a mutagenised peptide; and iii) solvation energies of two 6-heavy atom structural graphs. In contrast to typical data-error scaling, our results showed discontinuous monotonic phase transitions during learning, observed as rapid drops in the test error at particular thresholds of training data. We observed two learning regimes, which we call saturated and asymptotic decay, and found that they are conditioned by the level of complexity (i.e. number of mutations) enclosed in the training set. We show that during training on this class of problems, the predictions were clustered by the ML models employed in the calibration plots. Furthermore, we present an alternative strategy to normalize learning curves (LCs) and the concept of mutant based shuffling. This work has implications for machine learning on mutagenisable discrete spaces such as chemical properties or protein phenotype prediction, and improves basic understanding of concepts in statistical learning theory.

Encrypted machine learning of molecular quantum properties

Large machine learning models with improved predictions have become widely available in the chemical sciences. Unfortunately, these models do not protect the privacy necessary within commercial settings, prohibiting the use of potentially extremely valuable data by others. Encrypting the prediction process can solve this problem by double-blind model evaluation and prohibits the extraction of training or query data. However, contemporary ML models based on fully homomorphic encryption or federated learning are either too expensive for practical use or have to trade higher speed for weaker security. We have implemented secure and computationally feasible encrypted machine learning models using oblivious transfer enabling and secure predictions of molecular quantum properties across chemical compound space. However, we find that encrypted predictions using kernel ridge regression models are a million times more expensive than without encryption. This demonstrates a dire need for a compact machine learning model architecture, including molecular representation and kernel matrix size, that minimizes model evaluation costs.

Neural networks and kernel ridge regression for excited states dynamics of CH$_2$NH$_2^+$: From single-state to multi-state representations and multi-property machine learning models

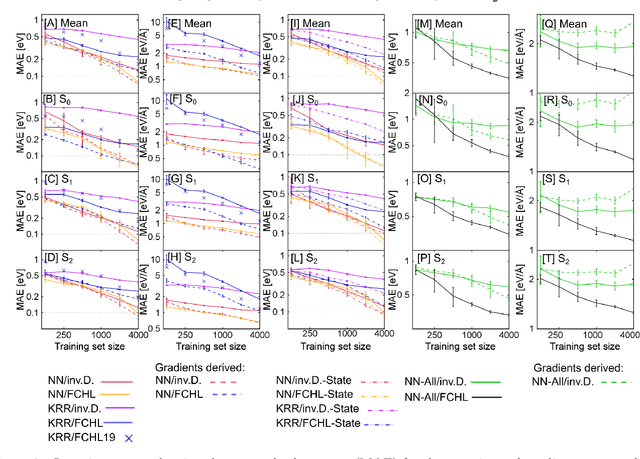
Excited-state dynamics simulations are a powerful tool to investigate photo-induced reactions of molecules and materials and provide complementary information to experiments. Since the applicability of these simulation techniques is limited by the costs of the underlying electronic structure calculations, we develop and assess different machine learning models for this task. The machine learning models are trained on {\emph ab initio} calculations for excited electronic states, using the methylenimmonium cation (CH$_2$NH$_2^+$) as a model system. For the prediction of excited-state properties, multiple outputs are desirable, which is straightforward with neural networks but less explored with kernel ridge regression. We overcome this challenge for kernel ridge regression in the case of energy predictions by encoding the electronic states explicitly in the inputs, in addition to the molecular representation. We adopt this strategy also for our neural networks for comparison. Such a state encoding enables not only kernel ridge regression with multiple outputs but leads also to more accurate machine learning models for state-specific properties. An important goal for excited-state machine learning models is their use in dynamics simulations, which needs not only state-specific information but also couplings, i.e., properties involving pairs of states. Accordingly, we investigate the performance of different models for such coupling elements. Furthermore, we explore how combining all properties in a single neural network affects the accuracy. As an ultimate test for our machine learning models, we carry out excited-state dynamics simulations based on the predicted energies, forces and couplings and, thus, show the scopes and possibilities of machine learning for the treatment of electronically excited states.

Constant Size Molecular Descriptors For Use With Machine Learning

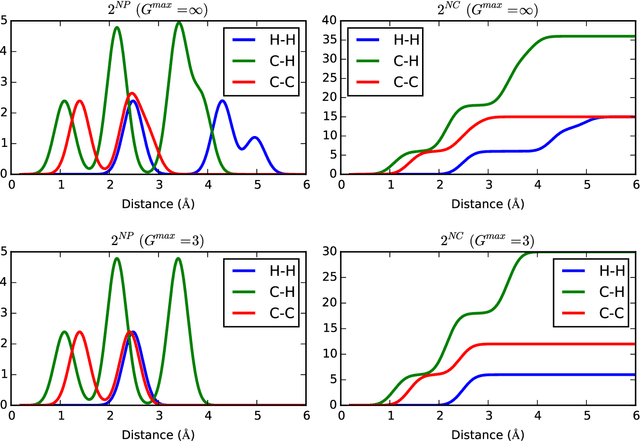
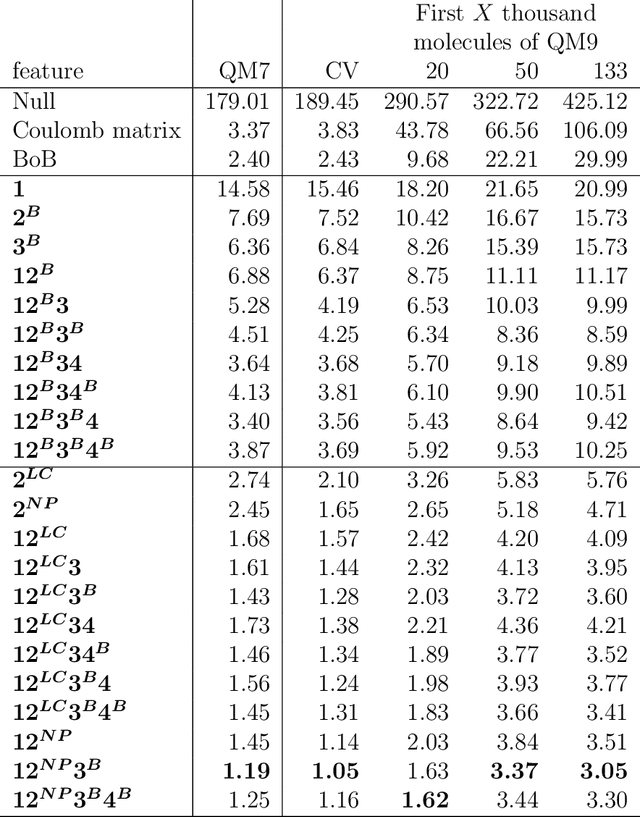
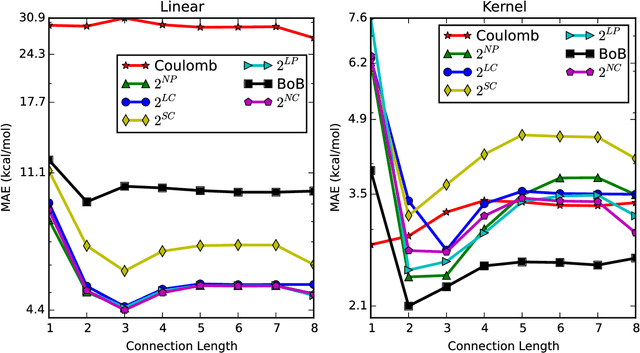
A set of molecular descriptors whose length is independent of molecular size is developed for machine learning models that target thermodynamic and electronic properties of molecules. These features are evaluated by monitoring performance of kernel ridge regression models on well-studied data sets of small organic molecules. The features include connectivity counts, which require only the bonding pattern of the molecule, and encoded distances, which summarize distances between both bonded and non-bonded atoms and so require the full molecular geometry. In addition to having constant size, these features summarize information regarding the local environment of atoms and bonds, such that models can take advantage of similarities resulting from the presence of similar chemical fragments across molecules. Combining these two types of features leads to models whose performance is comparable to or better than the current state of the art. The features introduced here have the advantage of leading to models that may be trained on smaller molecules and then used successfully on larger molecules.

Machine learning for many-body physics: efficient solution of dynamical mean-field theory

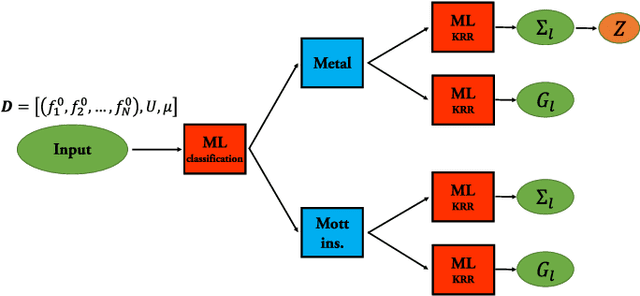
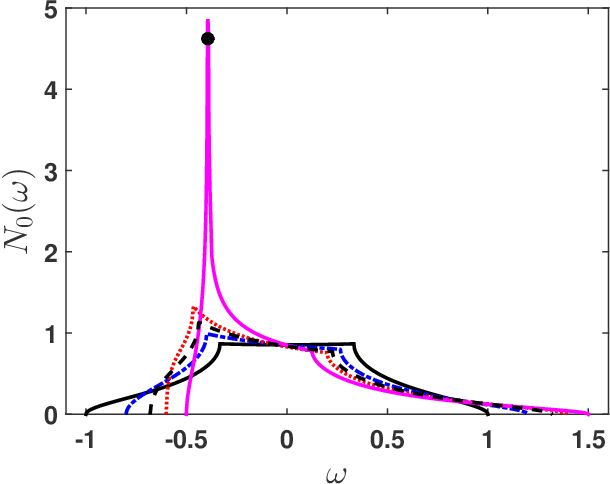
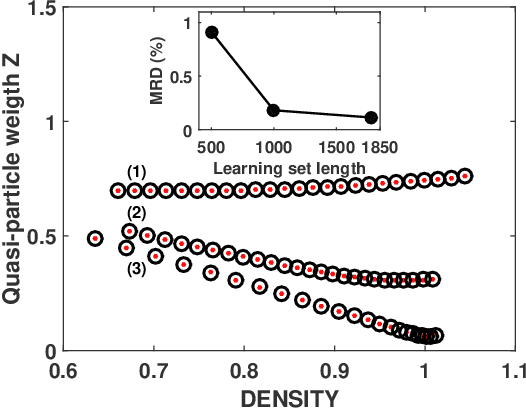
Machine learning methods for solving the equations of dynamical mean-field theory are developed. The method is demonstrated on the three dimensional Hubbard model. The key technical issues are defining a mapping of an input function to an output function, and distinguishing metallic from insulating solutions. Both metallic and Mott insulator solutions can be predicted. The validity of the machine learning scheme is assessed by comparing predictions of full correlation functions, of quasi-particle weight and particle density to values directly computed. The results indicate that with modest further development, machine learning approach may be an attractive computational efficient option for real materials predictions for strongly correlated systems.

Machine learning for many-body physics: The case of the Anderson impurity model

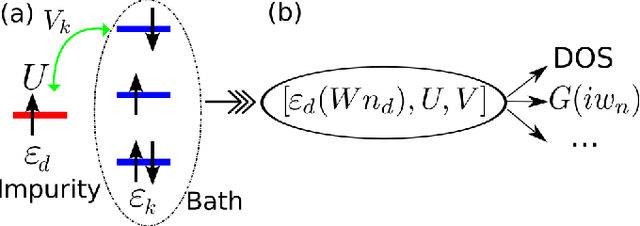
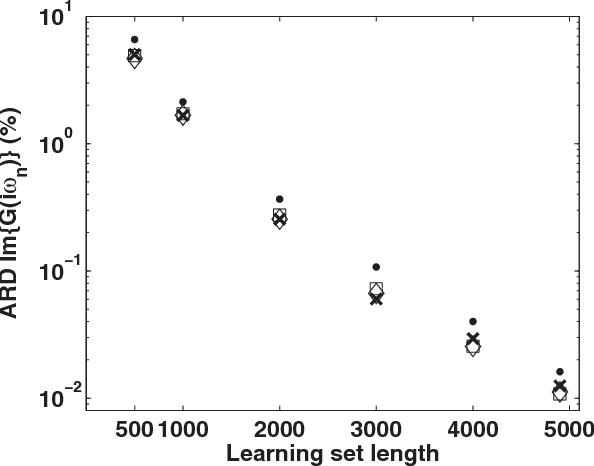
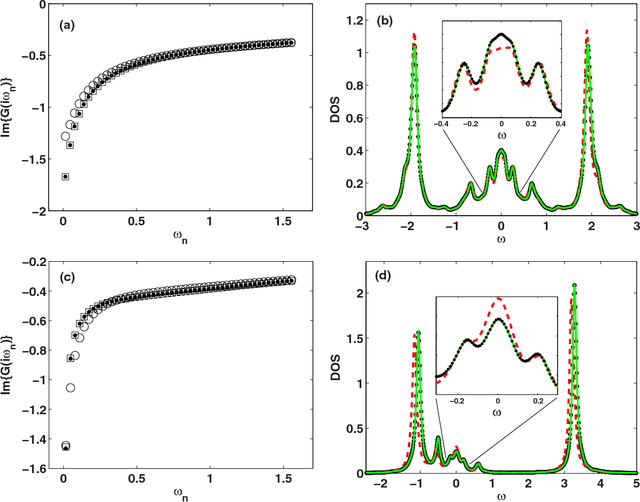
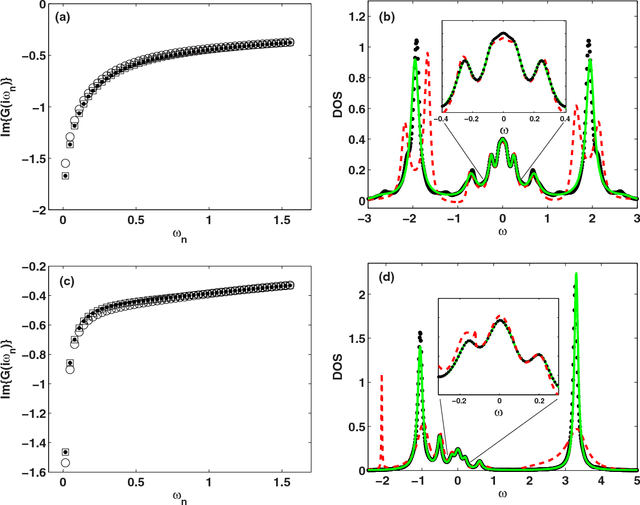
Machine learning methods are applied to finding the Green's function of the Anderson impurity model, a basic model system of quantum many-body condensed-matter physics. Different methods of parametrizing the Green's function are investigated; a representation in terms of Legendre polynomials is found to be superior due to its limited number of coefficients and its applicability to state of the art methods of solution. The dependence of the errors on the size of the training set is determined. The results indicate that a machine learning approach to dynamical mean-field theory may be feasible.

Fast and Accurate Modeling of Molecular Atomization Energies with Machine Learning

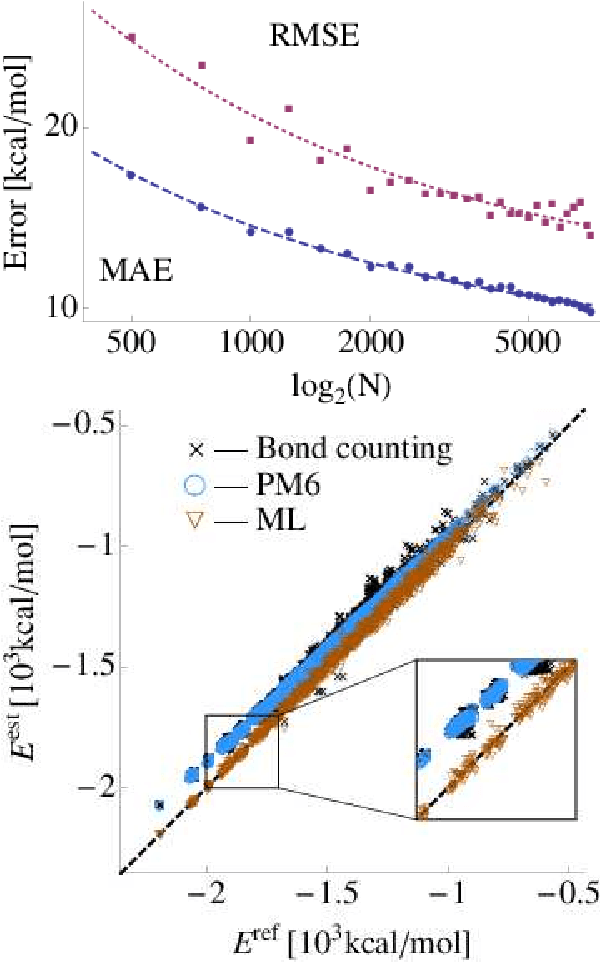
We introduce a machine learning model to predict atomization energies of a diverse set of organic molecules, based on nuclear charges and atomic positions only. The problem of solving the molecular Schr\"odinger equation is mapped onto a non-linear statistical regression problem of reduced complexity. Regression models are trained on and compared to atomization energies computed with hybrid density-functional theory. Cross-validation over more than seven thousand small organic molecules yields a mean absolute error of ~10 kcal/mol. Applicability is demonstrated for the prediction of molecular atomization potential energy curves.