Equivariant Matrix Function Neural Networks

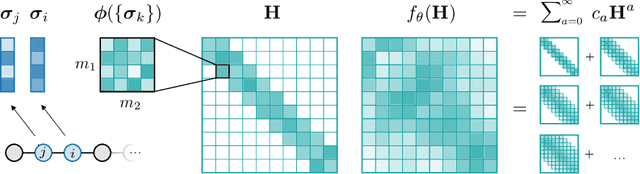
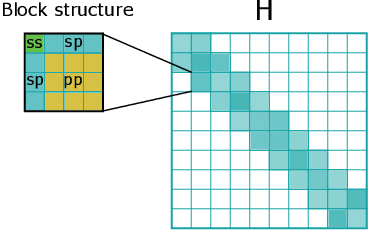
Graph Neural Networks (GNNs), especially message-passing neural networks (MPNNs), have emerged as powerful architectures for learning on graphs in diverse applications. However, MPNNs face challenges when modeling non-local interactions in systems such as large conjugated molecules, metals, or amorphous materials. Although Spectral GNNs and traditional neural networks such as recurrent neural networks and transformers mitigate these challenges, they often lack extensivity, adaptability, generalizability, computational efficiency, or fail to capture detailed structural relationships or symmetries in the data. To address these concerns, we introduce Matrix Function Neural Networks (MFNs), a novel architecture that parameterizes non-local interactions through analytic matrix equivariant functions. Employing resolvent expansions offers a straightforward implementation and the potential for linear scaling with system size. The MFN architecture achieves state-of-the-art performance in standard graph benchmarks, such as the ZINC and TU datasets, and is able to capture intricate non-local interactions in quantum systems, paving the way to new state-of-the-art force fields.

BenchML: an extensible pipelining framework for benchmarking representations of materials and molecules at scale

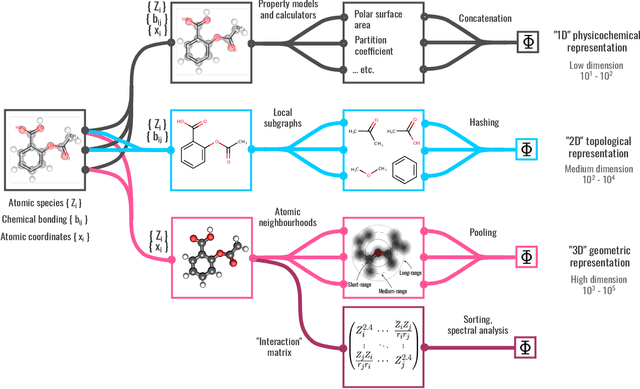
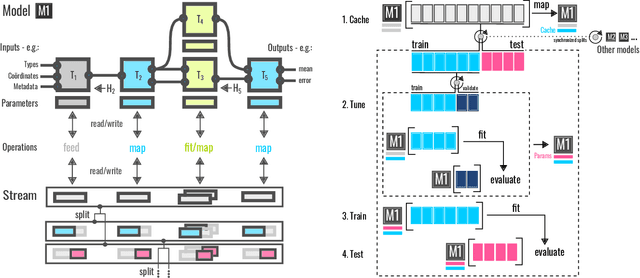
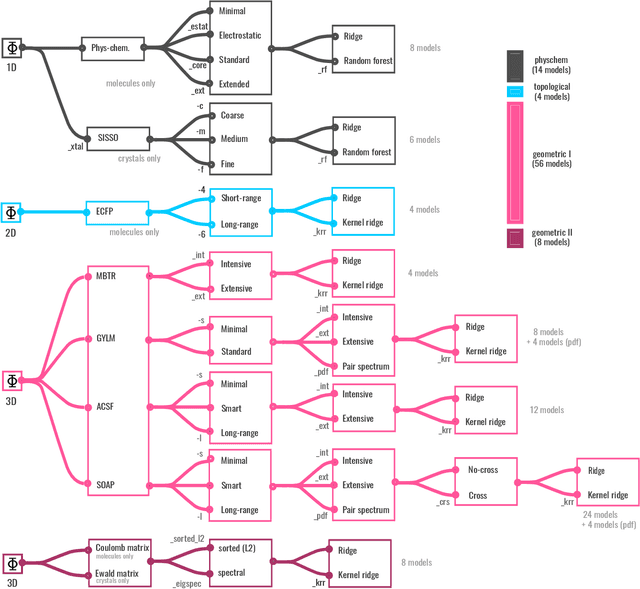
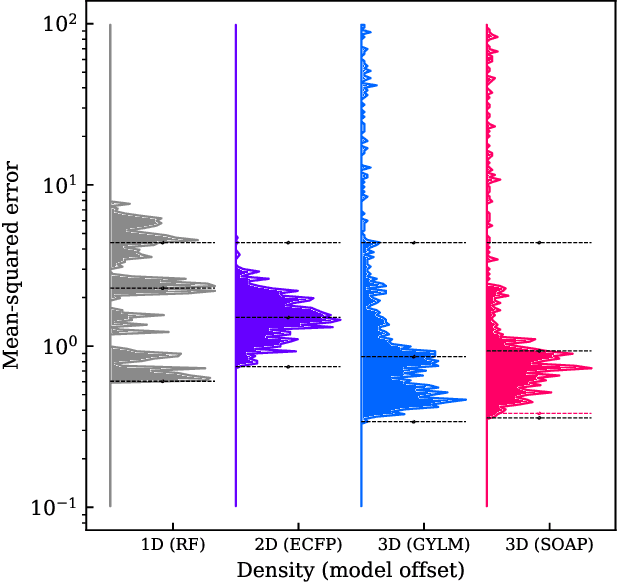
We introduce a machine-learning (ML) framework for high-throughput benchmarking of diverse representations of chemical systems against datasets of materials and molecules. The guiding principle underlying the benchmarking approach is to evaluate raw descriptor performance by limiting model complexity to simple regression schemes while enforcing best ML practices, allowing for unbiased hyperparameter optimization, and assessing learning progress through learning curves along series of synchronized train-test splits. The resulting models are intended as baselines that can inform future method development, next to indicating how easily a given dataset can be learnt. Through a comparative analysis of the training outcome across a diverse set of physicochemical, topological and geometric representations, we glean insight into the relative merits of these representations as well as their interrelatedness.

Neural networks and kernel ridge regression for excited states dynamics of CH$_2$NH$_2^+$: From single-state to multi-state representations and multi-property machine learning models

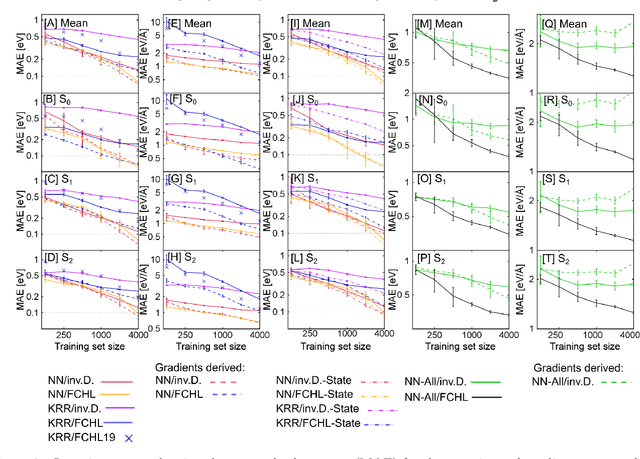
Excited-state dynamics simulations are a powerful tool to investigate photo-induced reactions of molecules and materials and provide complementary information to experiments. Since the applicability of these simulation techniques is limited by the costs of the underlying electronic structure calculations, we develop and assess different machine learning models for this task. The machine learning models are trained on {\emph ab initio} calculations for excited electronic states, using the methylenimmonium cation (CH$_2$NH$_2^+$) as a model system. For the prediction of excited-state properties, multiple outputs are desirable, which is straightforward with neural networks but less explored with kernel ridge regression. We overcome this challenge for kernel ridge regression in the case of energy predictions by encoding the electronic states explicitly in the inputs, in addition to the molecular representation. We adopt this strategy also for our neural networks for comparison. Such a state encoding enables not only kernel ridge regression with multiple outputs but leads also to more accurate machine learning models for state-specific properties. An important goal for excited-state machine learning models is their use in dynamics simulations, which needs not only state-specific information but also couplings, i.e., properties involving pairs of states. Accordingly, we investigate the performance of different models for such coupling elements. Furthermore, we explore how combining all properties in a single neural network affects the accuracy. As an ultimate test for our machine learning models, we carry out excited-state dynamics simulations based on the predicted energies, forces and couplings and, thus, show the scopes and possibilities of machine learning for the treatment of electronically excited states.