Bingqing Cheng
Machine learning interatomic potential can infer electrical response
Apr 07, 2025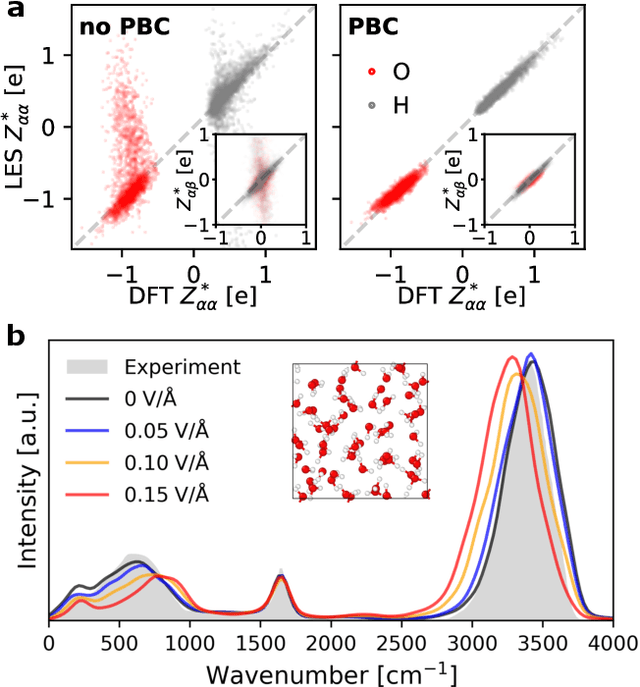
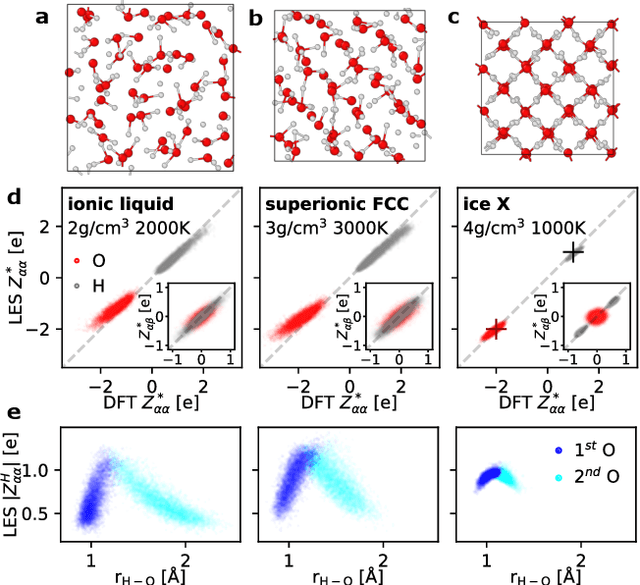
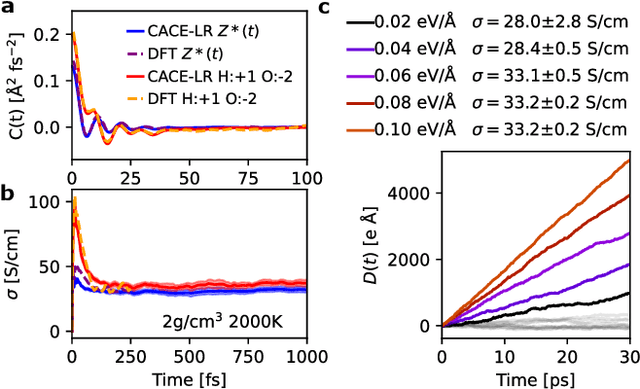
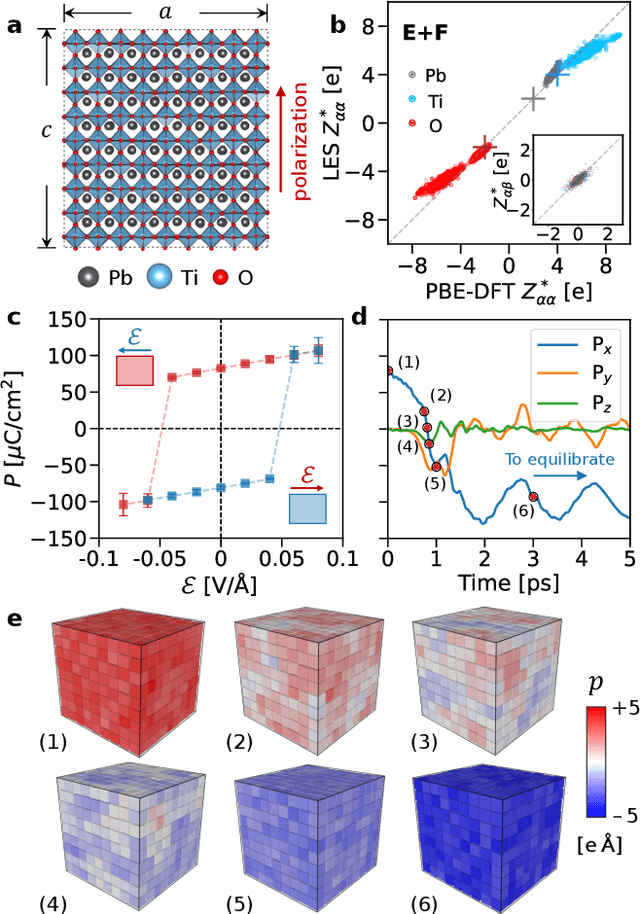
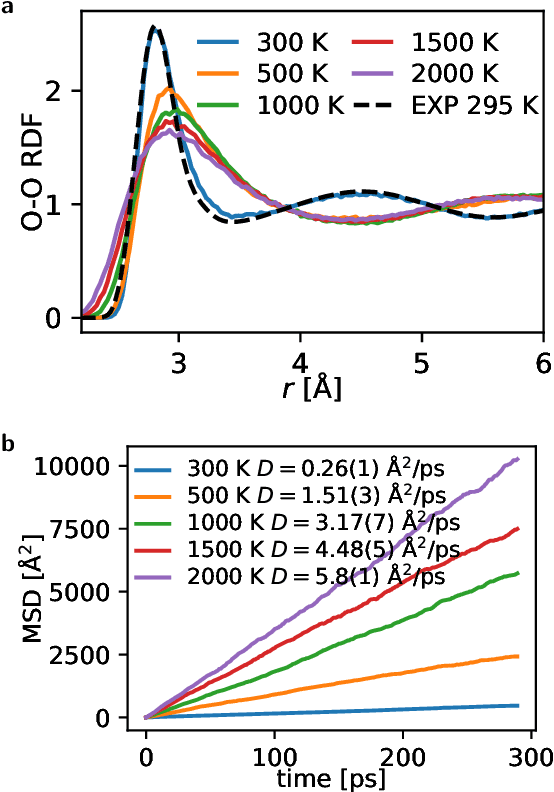
Abstract:Modeling the response of material and chemical systems to electric fields remains a longstanding challenge. Machine learning interatomic potentials (MLIPs) offer an efficient and scalable alternative to quantum mechanical methods but do not by themselves incorporate electrical response. Here, we show that polarization and Born effective charge (BEC) tensors can be directly extracted from long-range MLIPs within the Latent Ewald Summation (LES) framework, solely by learning from energy and force data. Using this approach, we predict the infrared spectra of bulk water under zero or finite external electric fields, ionic conductivities of high-pressure superionic ice, and the phase transition and hysteresis in ferroelectric PbTiO$_3$ perovskite. This work thus extends the capability of MLIPs to predict electrical response--without training on charges or polarization or BECs--and enables accurate modeling of electric-field-driven processes in diverse systems at scale.
Learning charges and long-range interactions from energies and forces
Dec 19, 2024



Abstract:Accurate modeling of long-range forces is critical in atomistic simulations, as they play a central role in determining the properties of materials and chemical systems. However, standard machine learning interatomic potentials (MLIPs) often rely on short-range approximations, limiting their applicability to systems with significant electrostatics and dispersion forces. We recently introduced the Latent Ewald Summation (LES) method, which captures long-range electrostatics without explicitly learning atomic charges or charge equilibration. Extending LES, we incorporate the ability to learn physical partial charges, encode charge states, and the option to impose charge neutrality constraints. We benchmark LES on diverse and challenging systems, including charged molecules, ionic liquid, electrolyte solution, polar dipeptides, surface adsorption, electrolyte/solid interfaces, and solid-solid interfaces. Our results show that LES can effectively infer physical partial charges, dipole and quadrupole moments, as well as achieve better accuracy compared to methods that explicitly learn charges. LES thus provides an efficient, interpretable, and generalizable MLIP framework for simulating complex systems with intricate charge transfer and long-range
Automatic feature selection and weighting using Differentiable Information Imbalance
Oct 30, 2024Abstract:Feature selection is a common process in many applications, but it is accompanied by uncertainties such as: What is the optimal dimensionality of an interpretable, reduced feature space to retain a maximum amount of information? How to account for different units of measure in features? How to weight different features according to their importance? To address these challenges, we introduce the Differentiable Information Imbalance (DII), an automatic data analysis method to rank information content between sets of features. Based on the nearest neighbors according to distances in the ground truth feature space, the method finds a low-dimensional subset of the input features, within which the pairwise distance relations are most similar to the ground truth. By employing the Differentiable Information Imbalance as a loss function, the relative feature weights of the inputs are optimized, simultaneously performing unit alignment and relative importance scaling, while preserving interpretability. Furthermore, this method can generate sparse solutions and determine the optimal size of the reduced feature space. We illustrate the usefulness of this approach on two prototypical benchmark problems: (1) Identifying a small set of collective variables capable of describing the conformational space of a biomolecule, and (2) selecting a subset of features for training a machine-learning force field. The results highlight the potential of the Differentiable Information Imbalance in addressing feature selection challenges and optimizing dimensionality in various applications. The method is implemented in the Python library DADApy.
Latent Ewald summation for machine learning of long-range interactions
Aug 27, 2024



Abstract:Machine learning interatomic potentials (MLIPs) often neglect long-range interactions, such as electrostatic and dispersion forces. In this work, we introduce a straightforward and efficient method to account for long-range interactions by learning a latent variable from local atomic descriptors and applying an Ewald summation to this variable. We demonstrate that in systems including charged, polar, or apolar molecular dimers, bulk water, and water-vapor interface, standard short-ranged MLIPs can lead to unphysical predictions even when employing message passing. The long-range models effectively eliminate these artifacts, with only about twice the computational cost of short-range MLIPs.
Response Matching for generating materials and molecules
May 15, 2024
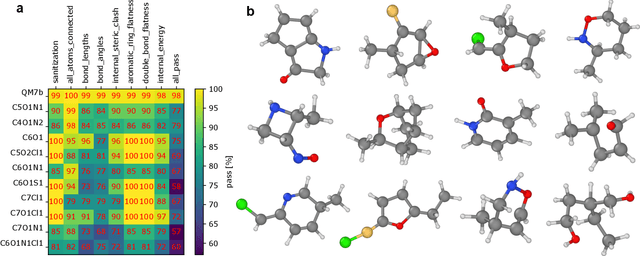

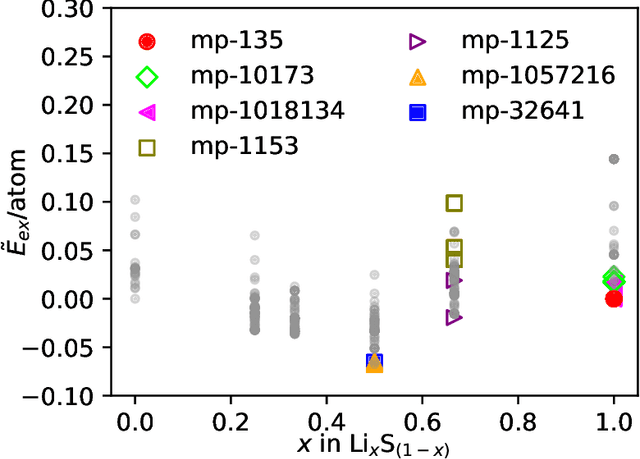
Abstract:Machine learning has recently emerged as a powerful tool for generating new molecular and material structures. The success of state-of-the-art models stems from their ability to incorporate physical symmetries, such as translation, rotation, and periodicity. Here, we present a novel generative method called Response Matching (RM), which leverages the fact that each stable material or molecule exists at the minimum of its potential energy surface. Consequently, any perturbation induces a response in energy and stress, driving the structure back to equilibrium. Matching to such response is closely related to score matching in diffusion models. By employing the combination of a machine learning interatomic potential and random structure search as the denoising model, RM exploits the locality of atomic interactions, and inherently respects permutation, translation, rotation, and periodic invariances. RM is the first model to handle both molecules and bulk materials under the same framework. We demonstrate the efficiency and generalization of RM across three systems: a small organic molecular dataset, stable crystals from the Materials Project, and one-shot learning on a single diamond configuration.
Cartesian atomic cluster expansion for machine learning interatomic potentials
Feb 12, 2024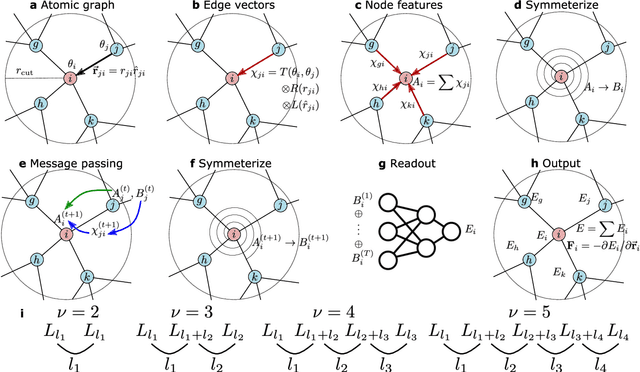
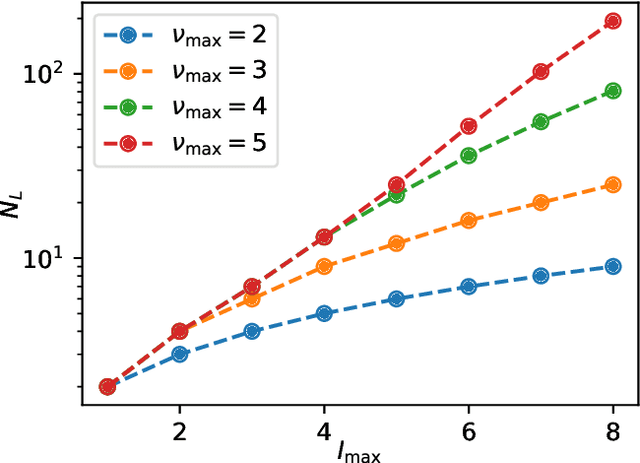
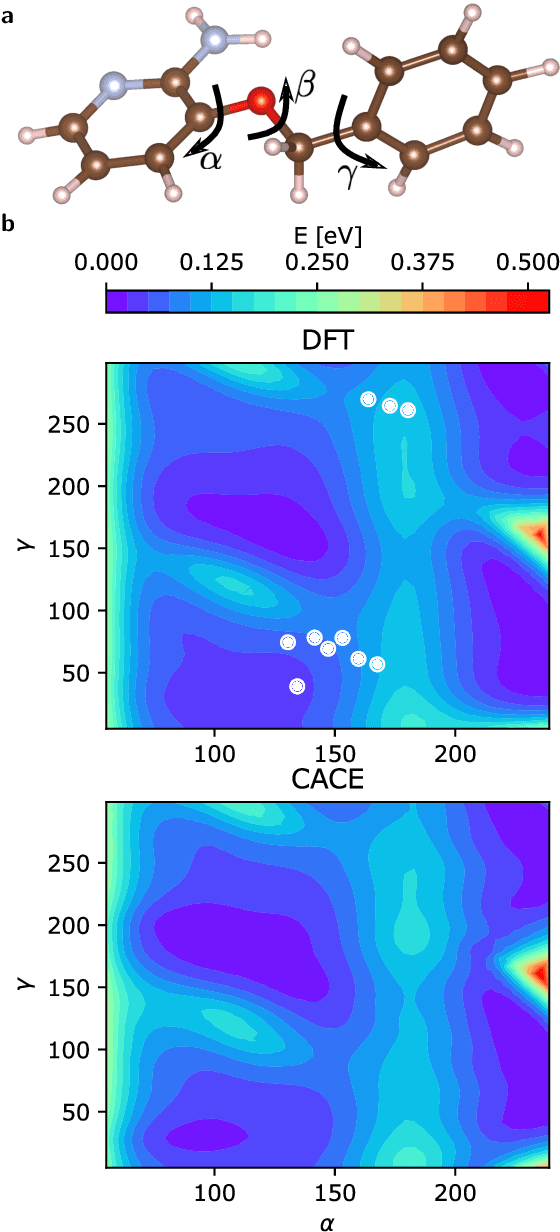
Abstract:Machine learning interatomic potentials are revolutionizing large-scale, accurate atomistic modelling in material science and chemistry. These potentials often use atomic cluster expansion or equivariant message passing with spherical harmonics as basis functions. However, the dependence on Clebsch-Gordan coefficients for maintaining rotational symmetry leads to computational inefficiencies and redundancies. We propose an alternative: a Cartesian-coordinates-based atomic density expansion. This approach provides a complete description of atomic environments while maintaining interaction body orders. Additionally, we integrate low-dimensional embeddings of various chemical elements and inter-atomic message passing. The resulting potential, named Cartesian Atomic Cluster Expansion (CACE), exhibits good accuracy, stability, and generalizability. We validate its performance in diverse systems, including bulk water, small molecules, and 25-element high-entropy alloys.
BenchML: an extensible pipelining framework for benchmarking representations of materials and molecules at scale
Dec 04, 2021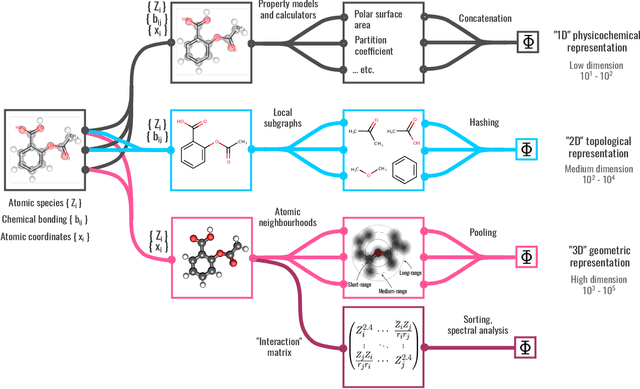
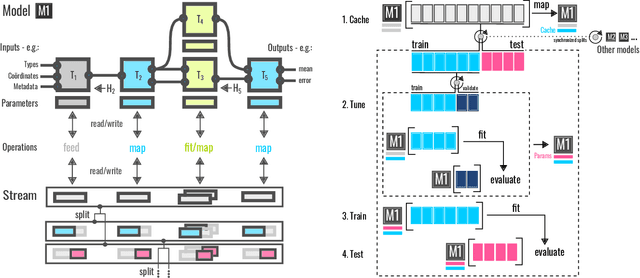
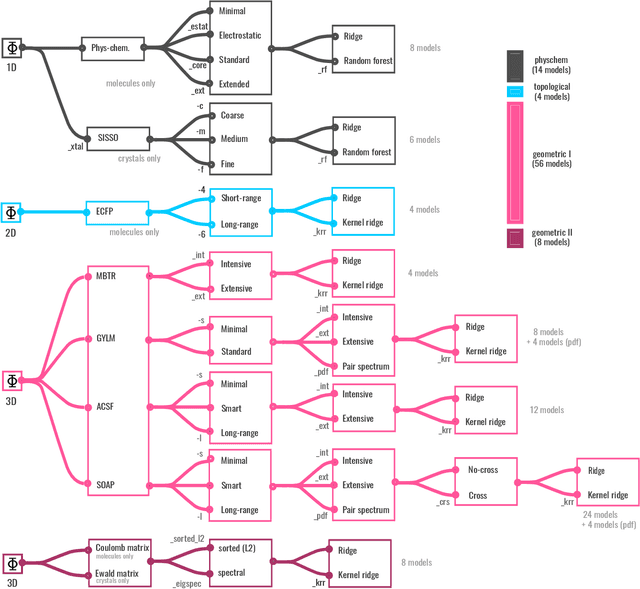
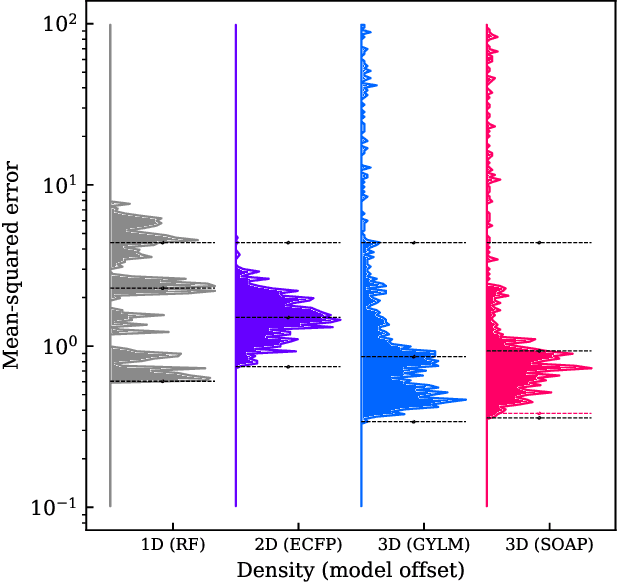
Abstract:We introduce a machine-learning (ML) framework for high-throughput benchmarking of diverse representations of chemical systems against datasets of materials and molecules. The guiding principle underlying the benchmarking approach is to evaluate raw descriptor performance by limiting model complexity to simple regression schemes while enforcing best ML practices, allowing for unbiased hyperparameter optimization, and assessing learning progress through learning curves along series of synchronized train-test splits. The resulting models are intended as baselines that can inform future method development, next to indicating how easily a given dataset can be learnt. Through a comparative analysis of the training outcome across a diverse set of physicochemical, topological and geometric representations, we glean insight into the relative merits of these representations as well as their interrelatedness.
Ranking the information content of distance measures
Apr 30, 2021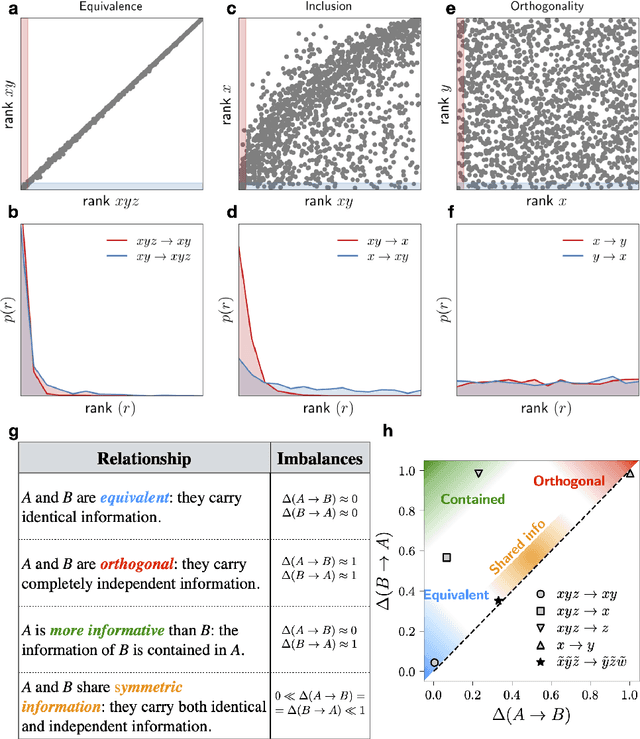
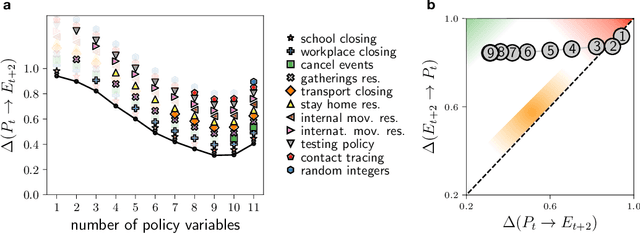
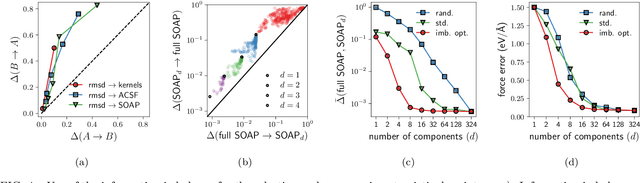
Abstract:Real-world data typically contain a large number of features that are often heterogeneous in nature, relevance, and also units of measure. When assessing the similarity between data points, one can build various distance measures using subsets of these features. Using the fewest features but still retaining sufficient information about the system is crucial in many statistical learning approaches, particularly when data are sparse. We introduce a statistical test that can assess the relative information retained when using two different distance measures, and determine if they are equivalent, independent, or if one is more informative than the other. This in turn allows finding the most informative distance measure out of a pool of candidates. The approach is applied to find the most relevant policy variables for controlling the Covid-19 epidemic and to find compact yet informative representations of atomic structures, but its potential applications are wide ranging in many branches of science.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge