Understanding Variational Autoencoders with Intrinsic Dimension and Information Imbalance

This work presents an analysis of the hidden representations of Variational Autoencoders (VAEs) using the Intrinsic Dimension (ID) and the Information Imbalance (II). We show that VAEs undergo a transition in behaviour once the bottleneck size is larger than the ID of the data, manifesting in a double hunchback ID profile and a qualitative shift in information processing as captured by the II. Our results also highlight two distinct training phases for architectures with sufficiently large bottleneck sizes, consisting of a rapid fit and a slower generalisation, as assessed by a differentiated behaviour of ID, II, and KL loss. These insights demonstrate that II and ID could be valuable tools for aiding architecture search, for diagnosing underfitting in VAEs, and, more broadly, they contribute to advancing a unified understanding of deep generative models through geometric analysis.

Density Estimation via Binless Multidimensional Integration

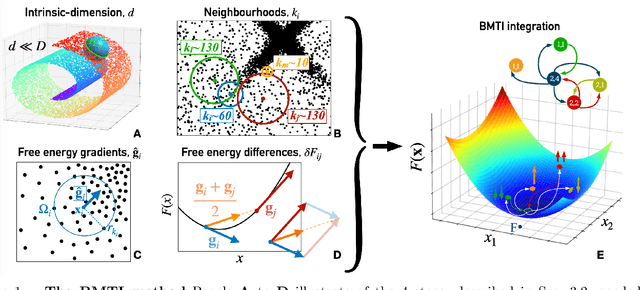
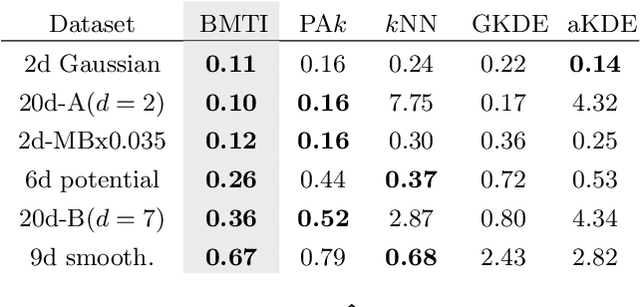
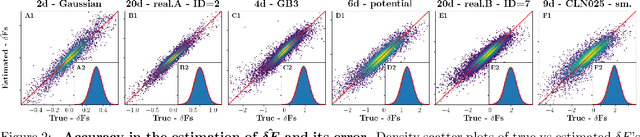
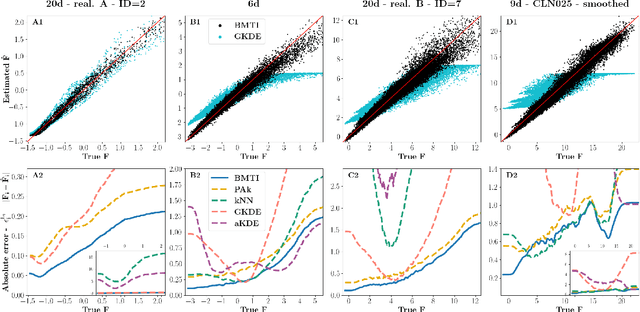
We introduce the Binless Multidimensional Thermodynamic Integration (BMTI) method for nonparametric, robust, and data-efficient density estimation. BMTI estimates the logarithm of the density by initially computing log-density differences between neighbouring data points. Subsequently, such differences are integrated, weighted by their associated uncertainties, using a maximum-likelihood formulation. This procedure can be seen as an extension to a multidimensional setting of the thermodynamic integration, a technique developed in statistical physics. The method leverages the manifold hypothesis, estimating quantities within the intrinsic data manifold without defining an explicit coordinate map. It does not rely on any binning or space partitioning, but rather on the construction of a neighbourhood graph based on an adaptive bandwidth selection procedure. BMTI mitigates the limitations commonly associated with traditional nonparametric density estimators, effectively reconstructing smooth profiles even in high-dimensional embedding spaces. The method is tested on a variety of complex synthetic high-dimensional datasets, where it is shown to outperform traditional estimators, and is benchmarked on realistic datasets from the chemical physics literature.

Beyond the noise: intrinsic dimension estimation with optimal neighbourhood identification

The Intrinsic Dimension (ID) is a key concept in unsupervised learning and feature selection, as it is a lower bound to the number of variables which are necessary to describe a system. However, in almost any real-world dataset the ID depends on the scale at which the data are analysed. Quite typically at a small scale, the ID is very large, as the data are affected by measurement errors. At large scale, the ID can also be erroneously large, due to the curvature and the topology of the manifold containing the data. In this work, we introduce an automatic protocol to select the sweet spot, namely the correct range of scales in which the ID is meaningful and useful. This protocol is based on imposing that for distances smaller than the correct scale the density of the data is constant. Since to estimate the density it is necessary to know the ID, this condition is imposed self-consistently. We illustrate the usefulness and robustness of this procedure by benchmarks on artificial and real-world datasets.

Simulating the economic impact of rationality through reinforcement learning and agent-based modelling

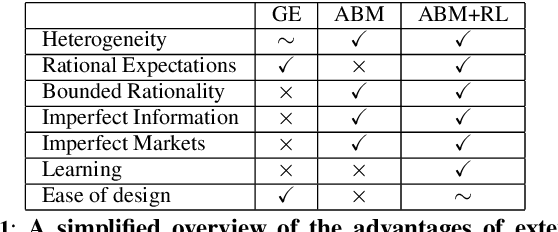
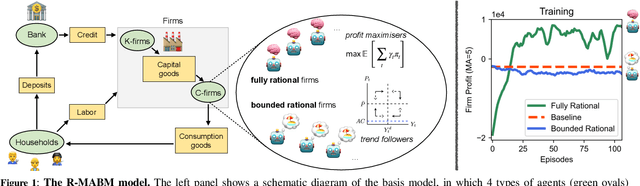
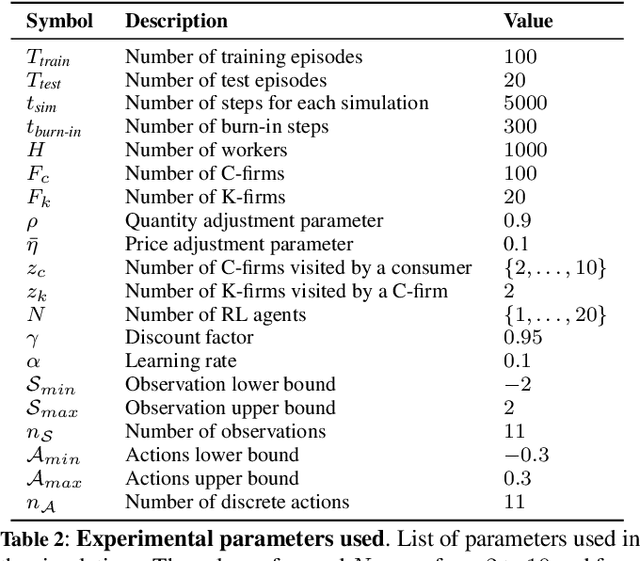
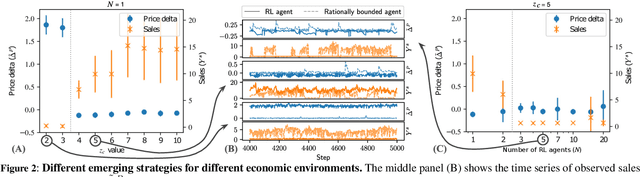
Agent-based models (ABMs) are simulation models used in economics to overcome some of the limitations of traditional frameworks based on general equilibrium assumptions. However, agents within an ABM follow predetermined, not fully rational, behavioural rules which can be cumbersome to design and difficult to justify. Here we leverage multi-agent reinforcement learning (RL) to expand the capabilities of ABMs with the introduction of fully rational agents that learn their policy by interacting with the environment and maximising a reward function. Specifically, we propose a 'Rational macro ABM' (R-MABM) framework by extending a paradigmatic macro ABM from the economic literature. We show that gradually substituting ABM firms in the model with RL agents, trained to maximise profits, allows for a thorough study of the impact of rationality on the economy. We find that RL agents spontaneously learn three distinct strategies for maximising profits, with the optimal strategy depending on the level of market competition and rationality. We also find that RL agents with independent policies, and without the ability to communicate with each other, spontaneously learn to segregate into different strategic groups, thus increasing market power and overall profits. Finally, we find that a higher degree of rationality in the economy always improves the macroeconomic environment as measured by total output, depending on the specific rational policy, this can come at the cost of higher instability. Our R-MABM framework is general, it allows for stable multi-agent learning, and represents a principled and robust direction to extend existing economic simulators.

Combining search strategies to improve performance in the calibration of economic ABMs

Calibrating agent-based models (ABMs) in economics and finance typically involves a derivative-free search in a very large parameter space. In this work, we benchmark a number of search methods in the calibration of a well-known macroeconomic ABM on real data, and further assess the performance of "mixed strategies" made by combining different methods. We find that methods based on random-forest surrogates are particularly efficient, and that combining search methods generally increases performance since the biases of any single method are mitigated. Moving from these observations, we propose a reinforcement learning (RL) scheme to automatically select and combine search methods on-the-fly during a calibration run. The RL agent keeps exploiting a specific method only as long as this keeps performing well, but explores new strategies when the specific method reaches a performance plateau. The resulting RL search scheme outperforms any other method or method combination tested, and does not rely on any prior information or trial and error procedure.

Intrinsic dimension estimation for discrete metrics

Real world-datasets characterized by discrete features are ubiquitous: from categorical surveys to clinical questionnaires, from unweighted networks to DNA sequences. Nevertheless, the most common unsupervised dimensional reduction methods are designed for continuous spaces, and their use for discrete spaces can lead to errors and biases. In this letter we introduce an algorithm to infer the intrinsic dimension (ID) of datasets embedded in discrete spaces. We demonstrate its accuracy on benchmark datasets, and we apply it to analyze a metagenomic dataset for species fingerprinting, finding a surprisingly small ID, of order 2. This suggests that evolutive pressure acts on a low-dimensional manifold despite the high-dimensionality of sequences' space.

Reconstruction and segmentation from sparse sequential X-ray measurements of wood logs

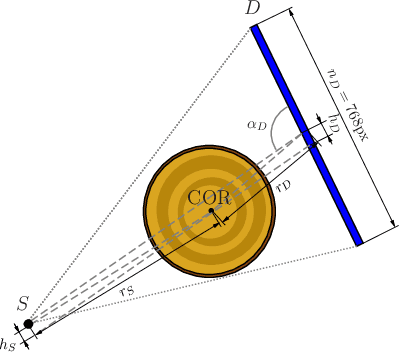
In industrial applications it is common to scan objects on a moving conveyor belt. If slice-wise 2D computed tomography (CT) measurements of the moving object are obtained we call it a sequential scanning geometry. In this case, each slice on its own does not carry sufficient information to reconstruct a useful tomographic image. Thus, here we propose the use of a Dimension reduced Kalman Filter to accumulate information between slices and allow for sufficiently accurate reconstructions for further assessment of the object. Additionally, we propose to use an unsupervised clustering approach known as Density Peak Advanced, to perform a segmentation and spot density anomalies in the internal structure of the reconstructed objects. We evaluate the method in a proof of concept study for the application of wood log scanning for the industrial sawing process, where the goal is to spot anomalies within the wood log to allow for optimal sawing patterns. Reconstruction and segmentation quality is evaluated from experimental measurement data for various scenarios of severely undersampled X-measurements. Results show clearly that an improvement of reconstruction quality can be obtained by employing the Dimension reduced Kalman Filter allowing to robustly obtain the segmented logs.

DADApy: Distance-based Analysis of DAta-manifolds in Python

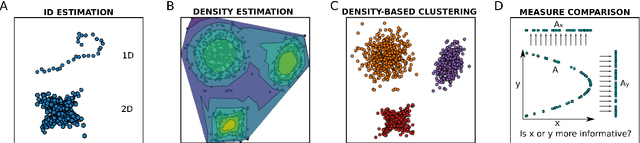
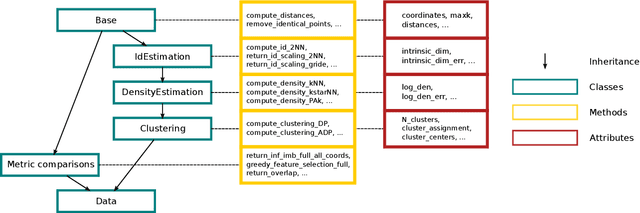
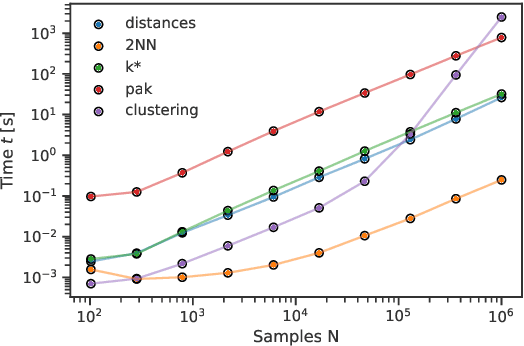
DADApy is a python software package for analysing and characterising high-dimensional data manifolds. It provides methods for estimating the intrinsic dimension and the probability density, for performing density-based clustering and for comparing different distance metrics. We review the main functionalities of the package and exemplify its usage in toy cases and in a real-world application. The package is freely available under the open-source Apache 2.0 license and can be downloaded from the Github page https://github.com/sissa-data-science/DADApy.

Representation mitosis in wide neural networks

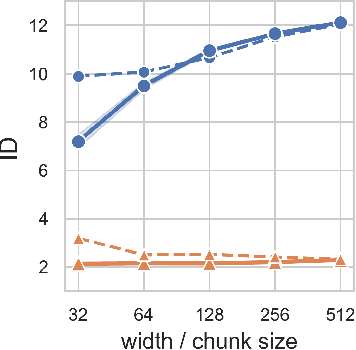
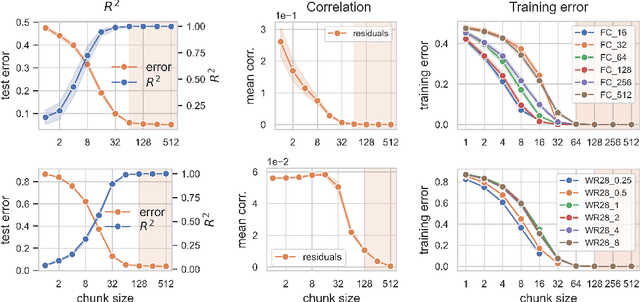
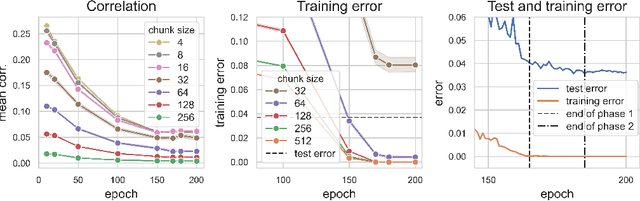
Deep neural networks (DNNs) defy the classical bias-variance trade-off: adding parameters to a DNN that exactly interpolates its training data will typically improve its generalisation performance. Explaining the mechanism behind the benefit of such over-parameterisation is an outstanding challenge for deep learning theory. Here, we study the last layer representation of various deep architectures such as Wide-ResNets for image classification and find evidence for an underlying mechanism that we call *representation mitosis*: if the last hidden representation is wide enough, its neurons tend to split into groups which carry identical information, and differ from each other only by a statistically independent noise. Like in a mitosis process, the number of such groups, or ``clones'', increases linearly with the width of the layer, but only if the width is above a critical value. We show that a key ingredient to activate mitosis is continuing the training process until the training error is zero. Finally, we show that in one of the learning tasks we considered, a wide model with several automatically developed clones performs significantly better than a deep ensemble based on architectures in which the last layer has the same size as the clones.

Ranking the information content of distance measures

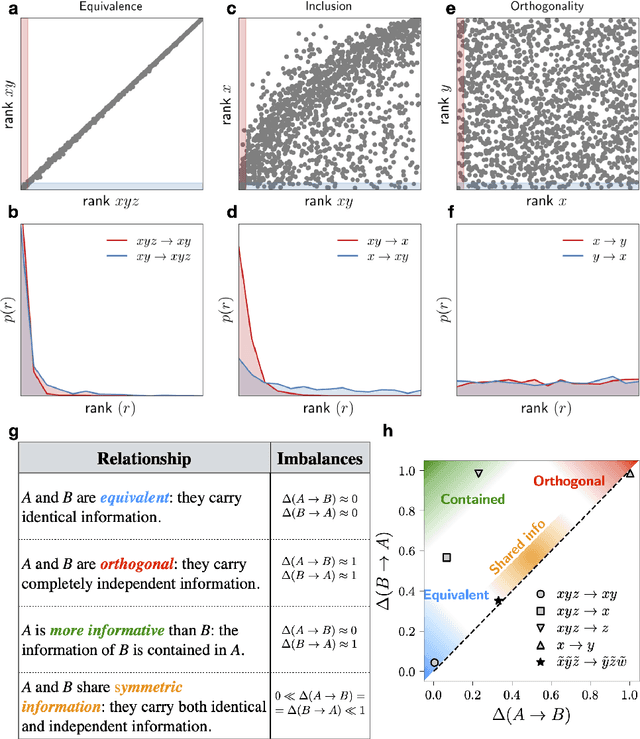
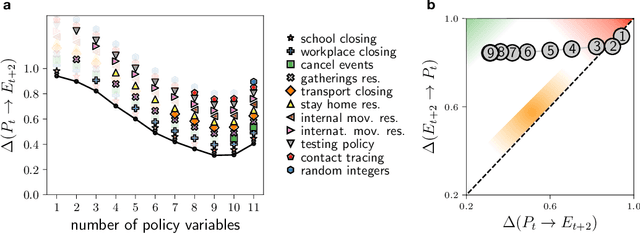
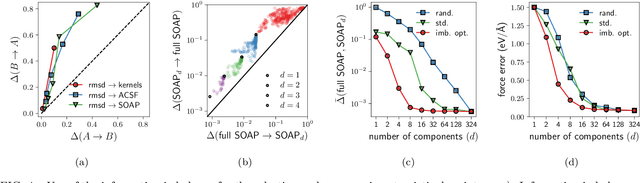
Real-world data typically contain a large number of features that are often heterogeneous in nature, relevance, and also units of measure. When assessing the similarity between data points, one can build various distance measures using subsets of these features. Using the fewest features but still retaining sufficient information about the system is crucial in many statistical learning approaches, particularly when data are sparse. We introduce a statistical test that can assess the relative information retained when using two different distance measures, and determine if they are equivalent, independent, or if one is more informative than the other. This in turn allows finding the most informative distance measure out of a pool of candidates. The approach is applied to find the most relevant policy variables for controlling the Covid-19 epidemic and to find compact yet informative representations of atomic structures, but its potential applications are wide ranging in many branches of science.