Computing Approximated Fixpoints via Dampened Mann Iteration

Fixpoints are ubiquitous in computer science and when dealing with quantitative semantics and verification one is commonly led to consider least fixpoints of (higher-dimensional) functions over the nonnegative reals. We show how to approximate the least fixpoint of such functions, focusing on the case in which they are not known precisely, but represented by a sequence of approximating functions that converge to them. We concentrate on monotone and non-expansive functions, for which uniqueness of fixpoints is not guaranteed and standard fixpoint iteration schemes might get stuck at a fixpoint that is not the least. Our main contribution is the identification of an iteration scheme, a variation of Mann iteration with a dampening factor, which, under suitable conditions, is shown to guarantee convergence to the least fixpoint of the function of interest. We then argue that these results are relevant in the context of model-based reinforcement learning for Markov decision processes (MDPs), showing that the proposed iteration scheme instantiates to MDPs and allows us to derive convergence to the optimal expected return. More generally, we show that our results can be used to iterate to the least fixpoint almost surely for systems where the function of interest can be approximated with given probabilistic error bounds, as it happens for probabilistic systems, such as simple stochastic games, that can be explored via sampling.

Simulating the economic impact of rationality through reinforcement learning and agent-based modelling

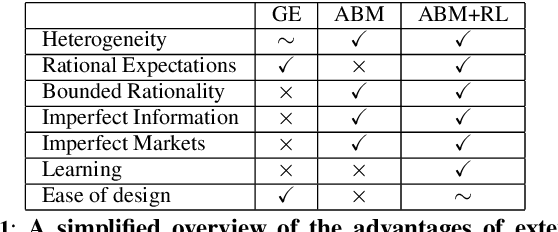
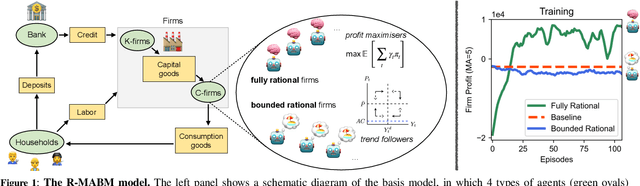
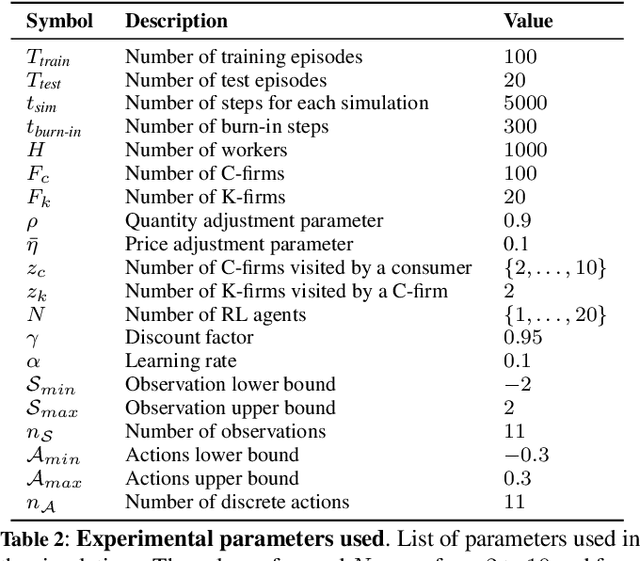
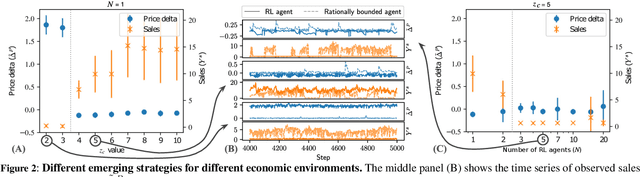
Agent-based models (ABMs) are simulation models used in economics to overcome some of the limitations of traditional frameworks based on general equilibrium assumptions. However, agents within an ABM follow predetermined, not fully rational, behavioural rules which can be cumbersome to design and difficult to justify. Here we leverage multi-agent reinforcement learning (RL) to expand the capabilities of ABMs with the introduction of fully rational agents that learn their policy by interacting with the environment and maximising a reward function. Specifically, we propose a 'Rational macro ABM' (R-MABM) framework by extending a paradigmatic macro ABM from the economic literature. We show that gradually substituting ABM firms in the model with RL agents, trained to maximise profits, allows for a thorough study of the impact of rationality on the economy. We find that RL agents spontaneously learn three distinct strategies for maximising profits, with the optimal strategy depending on the level of market competition and rationality. We also find that RL agents with independent policies, and without the ability to communicate with each other, spontaneously learn to segregate into different strategic groups, thus increasing market power and overall profits. Finally, we find that a higher degree of rationality in the economy always improves the macroeconomic environment as measured by total output, depending on the specific rational policy, this can come at the cost of higher instability. Our R-MABM framework is general, it allows for stable multi-agent learning, and represents a principled and robust direction to extend existing economic simulators.