Computing Fixpoints of Learned Functions: Chaotic Iteration and Simple Stochastic Games

The problem of determining the (least) fixpoint of (higher-dimensional) functions over the non-negative reals frequently occurs when dealing with systems endowed with a quantitative semantics. We focus on the situation in which the functions of interest are not known precisely but can only be approximated. As a first contribution we generalize an iteration scheme called dampened Mann iteration, recently introduced in the literature. The improved scheme relaxes previous constraints on parameter sequences, allowing learning rates to converge to zero or not converge at all. While seemingly minor, this flexibility is essential to enable the implementation of chaotic iterations, where only a subset of components is updated in each step, allowing to tackle higher-dimensional problems. Additionally, by allowing learning rates to converge to zero, we can relax conditions on the convergence speed of function approximations, making the method more adaptable to various scenarios. We also show that dampened Mann iteration applies immediately to compute the expected payoff in various probabilistic models, including simple stochastic games, not covered by previous work.

Computing Approximated Fixpoints via Dampened Mann Iteration

Fixpoints are ubiquitous in computer science and when dealing with quantitative semantics and verification one is commonly led to consider least fixpoints of (higher-dimensional) functions over the nonnegative reals. We show how to approximate the least fixpoint of such functions, focusing on the case in which they are not known precisely, but represented by a sequence of approximating functions that converge to them. We concentrate on monotone and non-expansive functions, for which uniqueness of fixpoints is not guaranteed and standard fixpoint iteration schemes might get stuck at a fixpoint that is not the least. Our main contribution is the identification of an iteration scheme, a variation of Mann iteration with a dampening factor, which, under suitable conditions, is shown to guarantee convergence to the least fixpoint of the function of interest. We then argue that these results are relevant in the context of model-based reinforcement learning for Markov decision processes (MDPs), showing that the proposed iteration scheme instantiates to MDPs and allows us to derive convergence to the optimal expected return. More generally, we show that our results can be used to iterate to the least fixpoint almost surely for systems where the function of interest can be approximated with given probabilistic error bounds, as it happens for probabilistic systems, such as simple stochastic games, that can be explored via sampling.

Interpretable Anomaly Detection via Discrete Optimization

Anomaly detection is essential in many application domains, such as cyber security, law enforcement, medicine, and fraud protection. However, the decision-making of current deep learning approaches is notoriously hard to understand, which often limits their practical applicability. To overcome this limitation, we propose a framework for learning inherently interpretable anomaly detectors from sequential data. More specifically, we consider the task of learning a deterministic finite automaton (DFA) from a given multi-set of unlabeled sequences. We show that this problem is computationally hard and develop two learning algorithms based on constraint optimization. Moreover, we introduce novel regularization schemes for our optimization problems that improve the overall interpretability of our DFAs. Using a prototype implementation, we demonstrate that our approach shows promising results in terms of accuracy and F1 score.

Probabilistic Systems with Hidden State and Unobservable Transitions

We consider probabilistic systems with hidden state and unobservable transitions, an extension of Hidden Markov Models (HMMs) that in particular admits unobservable {\epsilon}-transitions (also called null transitions), allowing state changes of which the observer is unaware. Due to the presence of {\epsilon}-loops this additional feature complicates the theory and requires to carefully set up the corresponding probability space and random variables. In particular we present an algorithm for determining the most probable explanation given an observation (a generalization of the Viterbi algorithm for HMMs) and a method for parameter learning that adapts the probabilities of a given model based on an observation (a generalization of the Baum-Welch algorithm). The latter algorithm guarantees that the given observation has a higher (or equal) probability after adjustment of the parameters and its correctness can be derived directly from the so-called EM algorithm.

Uncertainty Reasoning for Probabilistic Petri Nets via Bayesian Networks

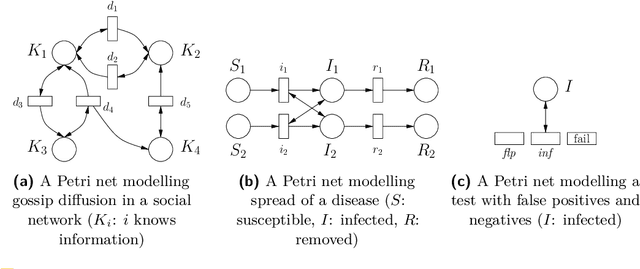
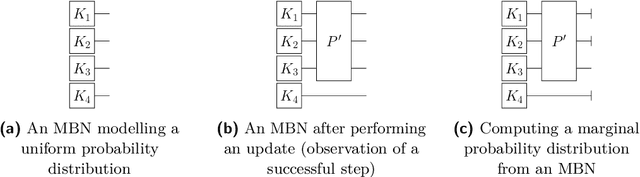
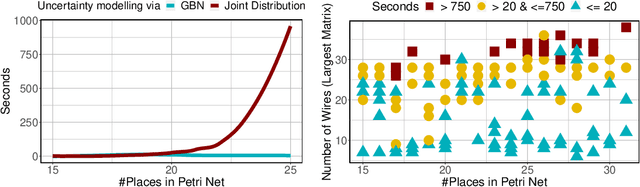
This paper exploits extended Bayesian networks for uncertainty reasoning on Petri nets, where firing of transitions is probabilistic. In particular, Bayesian networks are used as symbolic representations of probability distributions, modelling the observer's knowledge about the tokens in the net. The observer can study the net by monitoring successful and failed steps. An update mechanism for Bayesian nets is enabled by relaxing some of their restrictions, leading to modular Bayesian nets that can conveniently be represented and modified. As for every symbolic representation, the question is how to derive information - in this case marginal probability distributions - from a modular Bayesian net. We show how to do this by generalizing the known method of variable elimination. The approach is illustrated by examples about the spreading of diseases (SIR model) and information diffusion in social networks. We have implemented our approach and provide runtime results.