Probabilistic Systems with Hidden State and Unobservable Transitions

We consider probabilistic systems with hidden state and unobservable transitions, an extension of Hidden Markov Models (HMMs) that in particular admits unobservable {\epsilon}-transitions (also called null transitions), allowing state changes of which the observer is unaware. Due to the presence of {\epsilon}-loops this additional feature complicates the theory and requires to carefully set up the corresponding probability space and random variables. In particular we present an algorithm for determining the most probable explanation given an observation (a generalization of the Viterbi algorithm for HMMs) and a method for parameter learning that adapts the probabilities of a given model based on an observation (a generalization of the Baum-Welch algorithm). The latter algorithm guarantees that the given observation has a higher (or equal) probability after adjustment of the parameters and its correctness can be derived directly from the so-called EM algorithm.

Uncertainty Reasoning for Probabilistic Petri Nets via Bayesian Networks

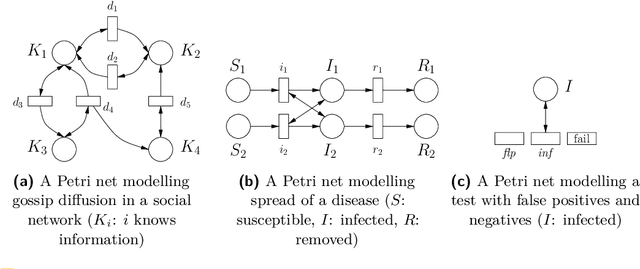
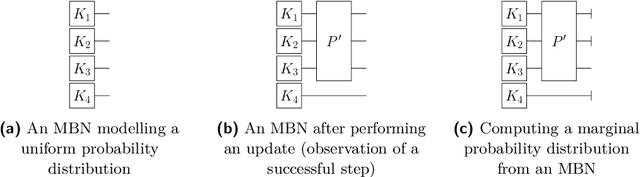
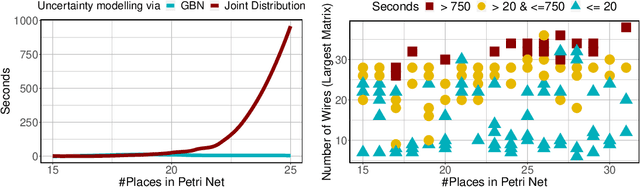
This paper exploits extended Bayesian networks for uncertainty reasoning on Petri nets, where firing of transitions is probabilistic. In particular, Bayesian networks are used as symbolic representations of probability distributions, modelling the observer's knowledge about the tokens in the net. The observer can study the net by monitoring successful and failed steps. An update mechanism for Bayesian nets is enabled by relaxing some of their restrictions, leading to modular Bayesian nets that can conveniently be represented and modified. As for every symbolic representation, the question is how to derive information - in this case marginal probability distributions - from a modular Bayesian net. We show how to do this by generalizing the known method of variable elimination. The approach is illustrated by examples about the spreading of diseases (SIR model) and information diffusion in social networks. We have implemented our approach and provide runtime results.