Head Pursuit: Probing Attention Specialization in Multimodal Transformers

Language and vision-language models have shown impressive performance across a wide range of tasks, but their internal mechanisms remain only partly understood. In this work, we study how individual attention heads in text-generative models specialize in specific semantic or visual attributes. Building on an established interpretability method, we reinterpret the practice of probing intermediate activations with the final decoding layer through the lens of signal processing. This lets us analyze multiple samples in a principled way and rank attention heads based on their relevance to target concepts. Our results show consistent patterns of specialization at the head level across both unimodal and multimodal transformers. Remarkably, we find that editing as few as 1% of the heads, selected using our method, can reliably suppress or enhance targeted concepts in the model output. We validate our approach on language tasks such as question answering and toxicity mitigation, as well as vision-language tasks including image classification and captioning. Our findings highlight an interpretable and controllable structure within attention layers, offering simple tools for understanding and editing large-scale generative models.

An unsupervised tour through the hidden pathways of deep neural networks

The goal of this thesis is to improve our understanding of the internal mechanisms by which deep artificial neural networks create meaningful representations and are able to generalize. We focus on the challenge of characterizing the semantic content of the hidden representations with unsupervised learning tools, partially developed by us and described in this thesis, which allow harnessing the low-dimensional structure of the data. Chapter 2. introduces Gride, a method that allows estimating the intrinsic dimension of the data as an explicit function of the scale without performing any decimation of the data set. Our approach is based on rigorous distributional results that enable the quantification of uncertainty of the estimates. Moreover, our method is simple and computationally efficient since it relies only on the distances among nearest data points. In Chapter 3, we study the evolution of the probability density across the hidden layers in some state-of-the-art deep neural networks. We find that the initial layers generate a unimodal probability density getting rid of any structure irrelevant to classification. In subsequent layers, density peaks arise in a hierarchical fashion that mirrors the semantic hierarchy of the concepts. This process leaves a footprint in the probability density of the output layer, where the topography of the peaks allows reconstructing the semantic relationships of the categories. In Chapter 4, we study the problem of generalization in deep neural networks: adding parameters to a network that interpolates its training data will typically improve its generalization performance, at odds with the classical bias-variance trade-off. We show that wide neural networks learn redundant representations instead of overfitting to spurious correlation and that redundant neurons appear only if the network is regularized and the training error is zero.

The Narrow Gate: Localized Image-Text Communication in Vision-Language Models

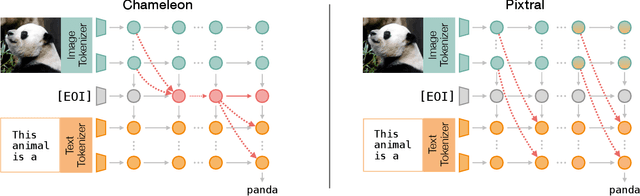
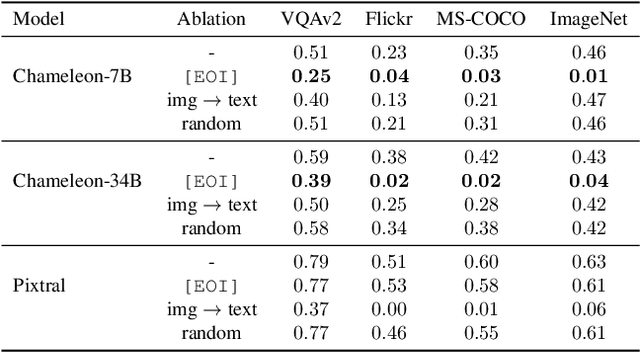
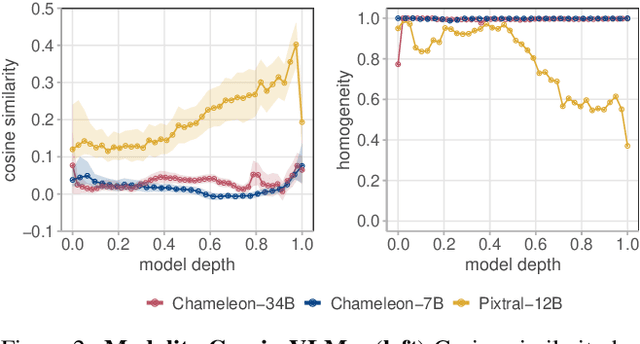
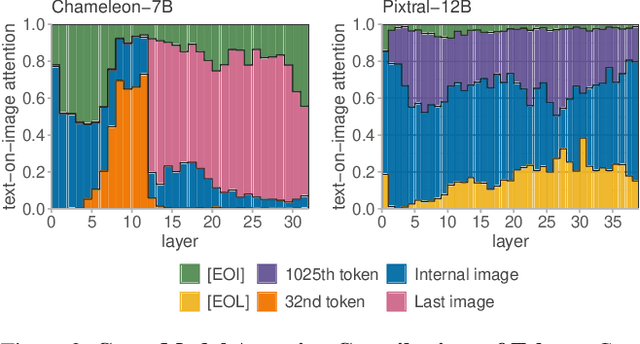
Recent advances in multimodal training have significantly improved the integration of image understanding and generation within a unified model. This study investigates how vision-language models (VLMs) handle image-understanding tasks, specifically focusing on how visual information is processed and transferred to the textual domain. We compare VLMs that generate both images and text with those that output only text, highlighting key differences in information flow. We find that in models with multimodal outputs, image and text embeddings are more separated within the residual stream. Additionally, models vary in how information is exchanged from visual to textual tokens. VLMs that only output text exhibit a distributed communication pattern, where information is exchanged through multiple image tokens. In contrast, models trained for image and text generation rely on a single token that acts as a narrow gate for the visual information. We demonstrate that ablating this single token significantly deteriorates performance on image understanding tasks. Furthermore, modifying this token enables effective steering of the image semantics, showing that targeted, local interventions can reliably control the model's global behavior.

Understanding Variational Autoencoders with Intrinsic Dimension and Information Imbalance

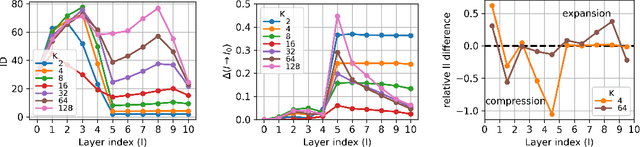
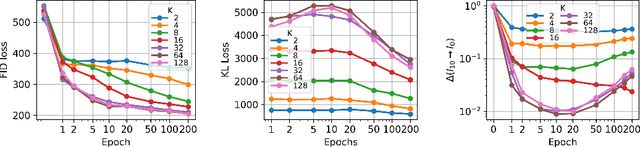
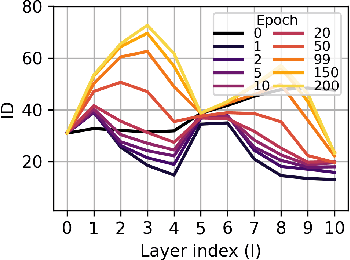
This work presents an analysis of the hidden representations of Variational Autoencoders (VAEs) using the Intrinsic Dimension (ID) and the Information Imbalance (II). We show that VAEs undergo a transition in behaviour once the bottleneck size is larger than the ID of the data, manifesting in a double hunchback ID profile and a qualitative shift in information processing as captured by the II. Our results also highlight two distinct training phases for architectures with sufficiently large bottleneck sizes, consisting of a rapid fit and a slower generalisation, as assessed by a differentiated behaviour of ID, II, and KL loss. These insights demonstrate that II and ID could be valuable tools for aiding architecture search, for diagnosing underfitting in VAEs, and, more broadly, they contribute to advancing a unified understanding of deep generative models through geometric analysis.

The representation landscape of few-shot learning and fine-tuning in large language models

In-context learning (ICL) and supervised fine-tuning (SFT) are two common strategies for improving the performance of modern large language models (LLMs) on specific tasks. Despite their different natures, these strategies often lead to comparable performance gains. However, little is known about whether they induce similar representations inside LLMs. We approach this problem by analyzing the probability landscape of their hidden representations in the two cases. More specifically, we compare how LLMs solve the same question-answering task, finding that ICL and SFT create very different internal structures, in both cases undergoing a sharp transition in the middle of the network. In the first half of the network, ICL shapes interpretable representations hierarchically organized according to their semantic content. In contrast, the probability landscape obtained with SFT is fuzzier and semantically mixed. In the second half of the model, the fine-tuned representations develop probability modes that better encode the identity of answers, while the landscape of ICL representations is characterized by less defined peaks. Our approach reveals the diverse computational strategies developed inside LLMs to solve the same task across different conditions, allowing us to make a step towards designing optimal methods to extract information from language models.

Emergence of a High-Dimensional Abstraction Phase in Language Transformers

A language model (LM) is a mapping from a linguistic context to an output token. However, much remains to be known about this mapping, including how its geometric properties relate to its function. We take a high-level geometric approach to its analysis, observing, across five pre-trained transformer-based LMs and three input datasets, a distinct phase characterized by high intrinsic dimensionality. During this phase, representations (1) correspond to the first full linguistic abstraction of the input; (2) are the first to viably transfer to downstream tasks; (3) predict each other across different LMs. Moreover, we find that an earlier onset of the phase strongly predicts better language modelling performance. In short, our results suggest that a central high-dimensionality phase underlies core linguistic processing in many common LM architectures.

Competition of Mechanisms: Tracing How Language Models Handle Facts and Counterfactuals

Interpretability research aims to bridge the gap between the empirical success and our scientific understanding of the inner workings of large language models (LLMs). However, most existing research in this area focused on analyzing a single mechanism, such as how models copy or recall factual knowledge. In this work, we propose the formulation of competition of mechanisms, which instead of individual mechanisms focuses on the interplay of multiple mechanisms, and traces how one of them becomes dominant in the final prediction. We uncover how and where the competition of mechanisms happens within LLMs using two interpretability methods, logit inspection and attention modification. Our findings show traces of the mechanisms and their competition across various model components, and reveal attention positions that effectively control the strength of certain mechanisms. Our code and data are at https://github.com/francescortu/Competition_of_Mechanisms.

Optimal transfer protocol by incremental layer defrosting

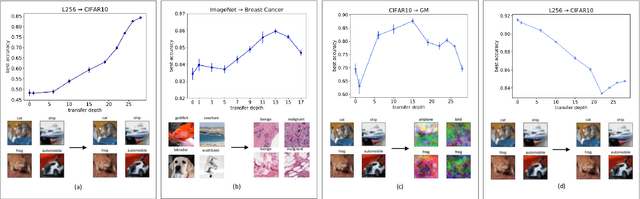
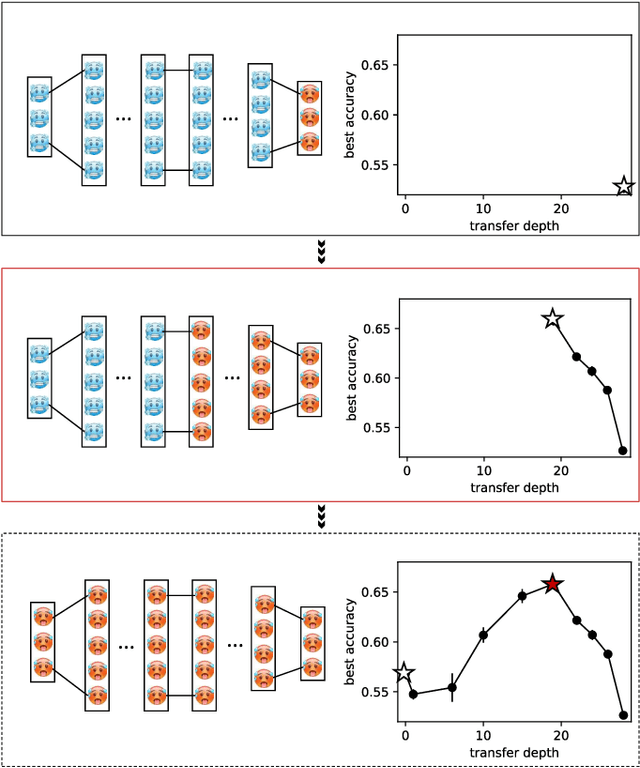
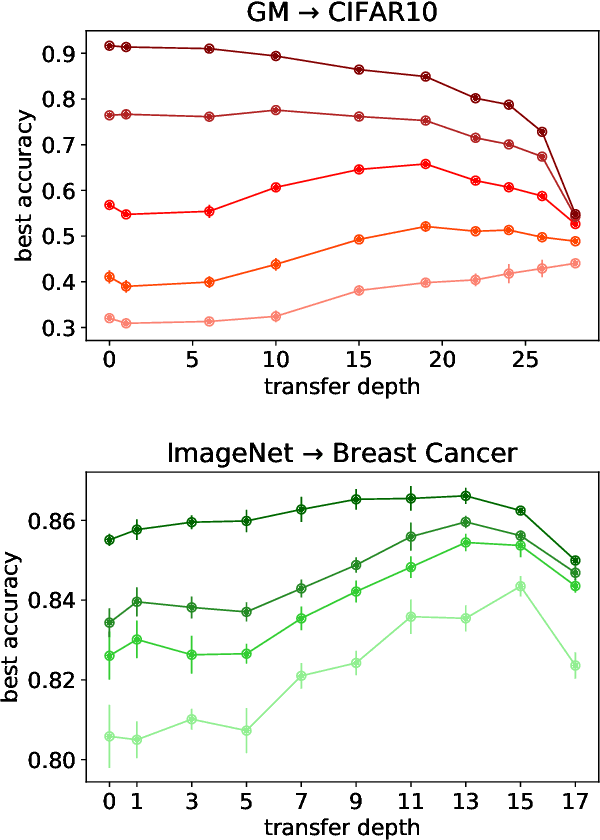
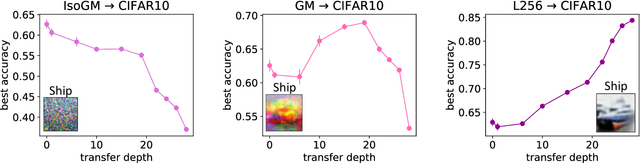
Transfer learning is a powerful tool enabling model training with limited amounts of data. This technique is particularly useful in real-world problems where data availability is often a serious limitation. The simplest transfer learning protocol is based on ``freezing" the feature-extractor layers of a network pre-trained on a data-rich source task, and then adapting only the last layers to a data-poor target task. This workflow is based on the assumption that the feature maps of the pre-trained model are qualitatively similar to the ones that would have been learned with enough data on the target task. In this work, we show that this protocol is often sub-optimal, and the largest performance gain may be achieved when smaller portions of the pre-trained network are kept frozen. In particular, we make use of a controlled framework to identify the optimal transfer depth, which turns out to depend non-trivially on the amount of available training data and on the degree of source-target task correlation. We then characterize transfer optimality by analyzing the internal representations of two networks trained from scratch on the source and the target task through multiple established similarity measures.

The geometry of hidden representations of large transformer models

Large transformers are powerful architectures for self-supervised analysis of data of various nature, ranging from protein sequences to text to images. In these models, the data representation in the hidden layers live in the same space, and the semantic structure of the dataset emerges by a sequence of functionally identical transformations between one representation and the next. We here characterize the geometric and statistical properties of these representations, focusing on the evolution of such proprieties across the layers. By analyzing geometric properties such as the intrinsic dimension (ID) and the neighbor composition we find that the representations evolve in a strikingly similar manner in transformers trained on protein language tasks and image reconstruction tasks. In the first layers, the data manifold expands, becoming high-dimensional, and then it contracts significantly in the intermediate layers. In the last part of the model, the ID remains approximately constant or forms a second shallow peak. We show that the semantic complexity of the dataset emerges at the end of the first peak. This phenomenon can be observed across many models trained on diverse datasets. Based on these observations, we suggest using the ID profile as an unsupervised proxy to identify the layers which are more suitable for downstream learning tasks.

DADApy: Distance-based Analysis of DAta-manifolds in Python

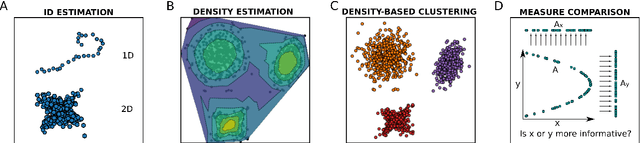
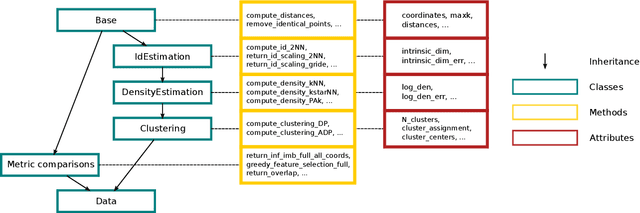
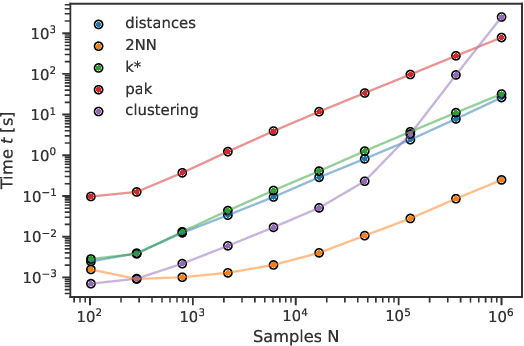
DADApy is a python software package for analysing and characterising high-dimensional data manifolds. It provides methods for estimating the intrinsic dimension and the probability density, for performing density-based clustering and for comparing different distance metrics. We review the main functionalities of the package and exemplify its usage in toy cases and in a real-world application. The package is freely available under the open-source Apache 2.0 license and can be downloaded from the Github page https://github.com/sissa-data-science/DADApy.