A Theory of Initialisation's Impact on Specialisation

Prior work has demonstrated a consistent tendency in neural networks engaged in continual learning tasks, wherein intermediate task similarity results in the highest levels of catastrophic interference. This phenomenon is attributed to the network's tendency to reuse learned features across tasks. However, this explanation heavily relies on the premise that neuron specialisation occurs, i.e. the emergence of localised representations. Our investigation challenges the validity of this assumption. Using theoretical frameworks for the analysis of neural networks, we show a strong dependence of specialisation on the initial condition. More precisely, we show that weight imbalance and high weight entropy can favour specialised solutions. We then apply these insights in the context of continual learning, first showing the emergence of a monotonic relation between task-similarity and forgetting in non-specialised networks. {Finally, we show that specialization by weight imbalance is beneficial on the commonly employed elastic weight consolidation regularisation technique.

Optimal Protocols for Continual Learning via Statistical Physics and Control Theory

Artificial neural networks often struggle with catastrophic forgetting when learning multiple tasks sequentially, as training on new tasks degrades the performance on previously learned ones. Recent theoretical work has addressed this issue by analysing learning curves in synthetic frameworks under predefined training protocols. However, these protocols relied on heuristics and lacked a solid theoretical foundation assessing their optimality. In this paper, we fill this gap combining exact equations for training dynamics, derived using statistical physics techniques, with optimal control methods. We apply this approach to teacher-student models for continual learning and multi-task problems, obtaining a theory for task-selection protocols maximising performance while minimising forgetting. Our theoretical analysis offers non-trivial yet interpretable strategies for mitigating catastrophic forgetting, shedding light on how optimal learning protocols can modulate established effects, such as the influence of task similarity on forgetting. Finally, we validate our theoretical findings on real-world data.

Tilting the Odds at the Lottery: the Interplay of Overparameterisation and Curricula in Neural Networks

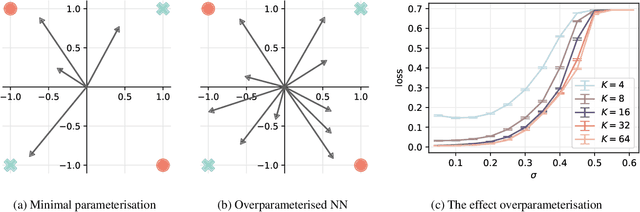
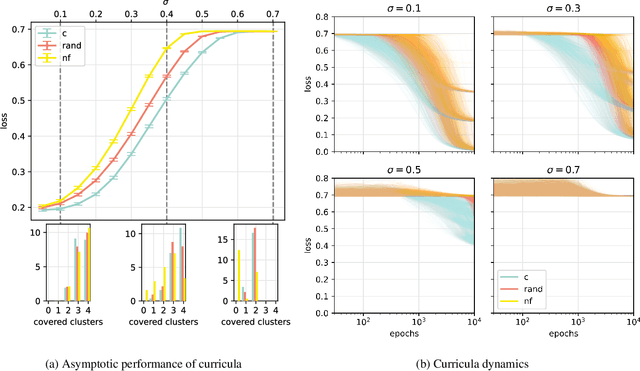
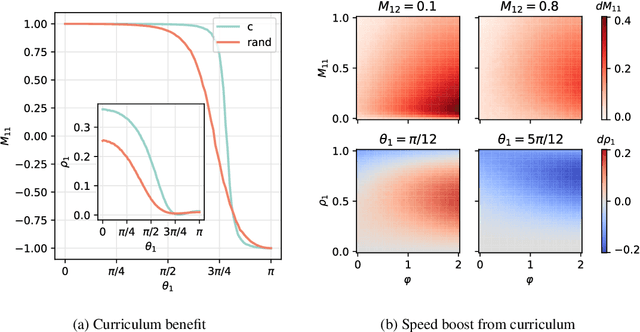
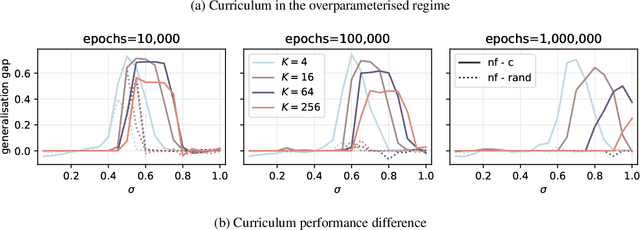
A wide range of empirical and theoretical works have shown that overparameterisation can amplify the performance of neural networks. According to the lottery ticket hypothesis, overparameterised networks have an increased chance of containing a sub-network that is well-initialised to solve the task at hand. A more parsimonious approach, inspired by animal learning, consists in guiding the learner towards solving the task by curating the order of the examples, i.e. providing a curriculum. However, this learning strategy seems to be hardly beneficial in deep learning applications. In this work, we undertake an analytical study that connects curriculum learning and overparameterisation. In particular, we investigate their interplay in the online learning setting for a 2-layer network in the XOR-like Gaussian Mixture problem. Our results show that a high degree of overparameterisation -- while simplifying the problem -- can limit the benefit from curricula, providing a theoretical account of the ineffectiveness of curricula in deep learning.

Bias in Motion: Theoretical Insights into the Dynamics of Bias in SGD Training

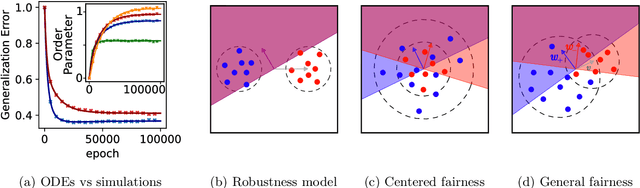
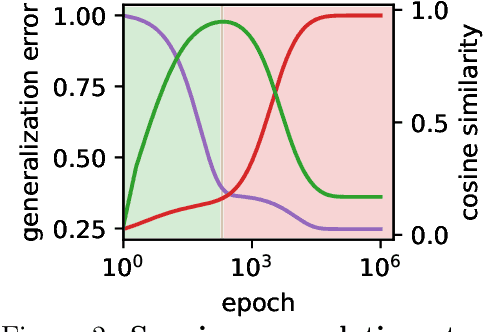
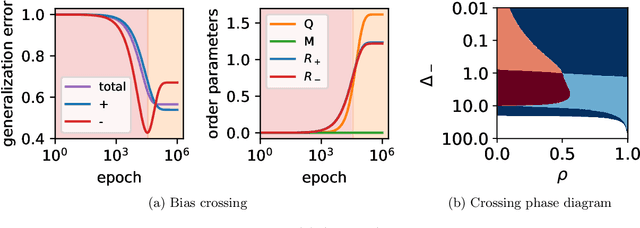
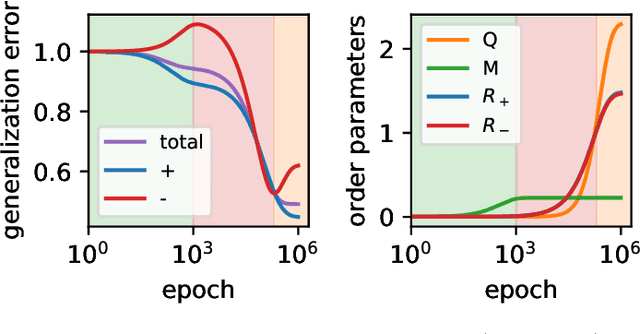
Machine learning systems often acquire biases by leveraging undesired features in the data, impacting accuracy variably across different sub-populations. Current understanding of bias formation mostly focuses on the initial and final stages of learning, leaving a gap in knowledge regarding the transient dynamics. To address this gap, this paper explores the evolution of bias in a teacher-student setup modeling different data sub-populations with a Gaussian-mixture model. We provide an analytical description of the stochastic gradient descent dynamics of a linear classifier in this setting, which we prove to be exact in high dimension. Notably, our analysis reveals how different properties of sub-populations influence bias at different timescales, showing a shifting preference of the classifier during training. Applying our findings to fairness and robustness, we delineate how and when heterogeneous data and spurious features can generate and amplify bias. We empirically validate our results in more complex scenarios by training deeper networks on synthetic and real datasets, including CIFAR10, MNIST, and CelebA.

The RL Perceptron: Generalisation Dynamics of Policy Learning in High Dimensions

Reinforcement learning (RL) algorithms have proven transformative in a range of domains. To tackle real-world domains, these systems often use neural networks to learn policies directly from pixels or other high-dimensional sensory input. By contrast, much theory of RL has focused on discrete state spaces or worst-case analysis, and fundamental questions remain about the dynamics of policy learning in high-dimensional settings. Here, we propose a solvable high-dimensional model of RL that can capture a variety of learning protocols, and derive its typical dynamics as a set of closed-form ordinary differential equations (ODEs). We derive optimal schedules for the learning rates and task difficulty - analogous to annealing schemes and curricula during training in RL - and show that the model exhibits rich behaviour, including delayed learning under sparse rewards; a variety of learning regimes depending on reward baselines; and a speed-accuracy trade-off driven by reward stringency. Experiments on variants of the Procgen game "Bossfight" and Arcade Learning Environment game "Pong" also show such a speed-accuracy trade-off in practice. Together, these results take a step towards closing the gap between theory and practice in high-dimensional RL.

Optimal transfer protocol by incremental layer defrosting

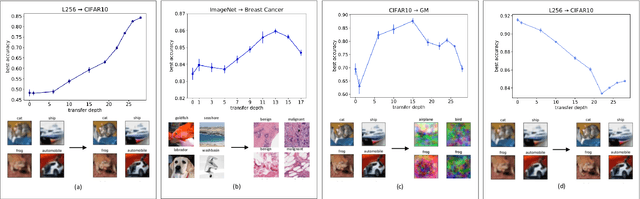
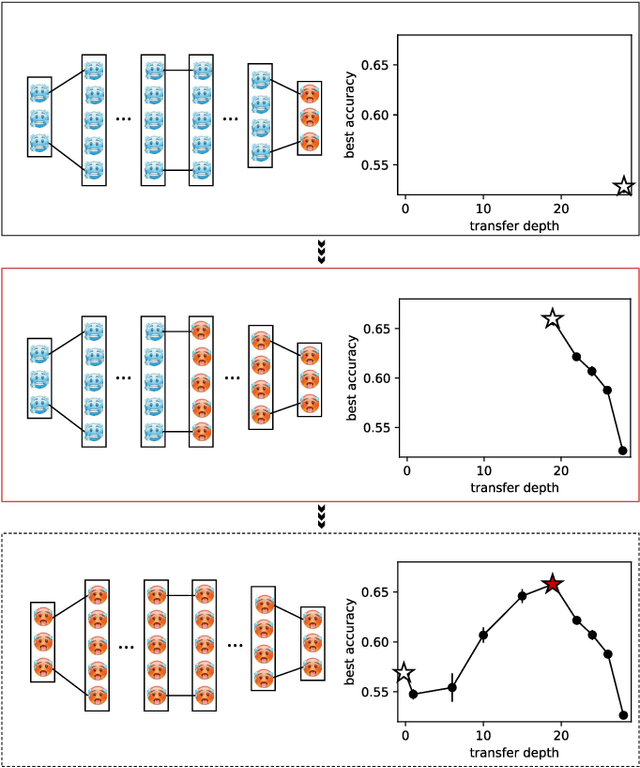
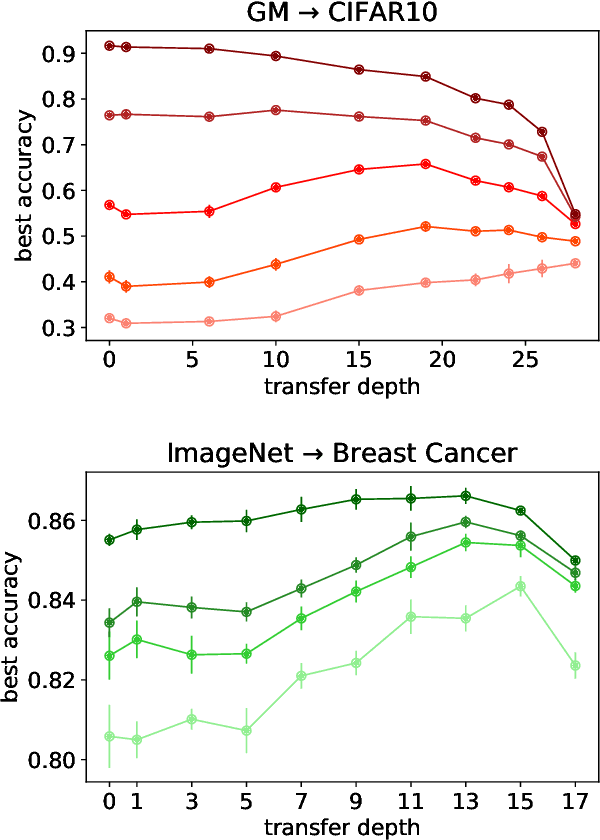
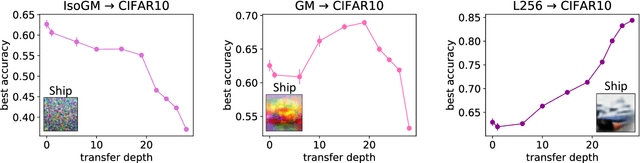
Transfer learning is a powerful tool enabling model training with limited amounts of data. This technique is particularly useful in real-world problems where data availability is often a serious limitation. The simplest transfer learning protocol is based on ``freezing" the feature-extractor layers of a network pre-trained on a data-rich source task, and then adapting only the last layers to a data-poor target task. This workflow is based on the assumption that the feature maps of the pre-trained model are qualitatively similar to the ones that would have been learned with enough data on the target task. In this work, we show that this protocol is often sub-optimal, and the largest performance gain may be achieved when smaller portions of the pre-trained network are kept frozen. In particular, we make use of a controlled framework to identify the optimal transfer depth, which turns out to depend non-trivially on the amount of available training data and on the degree of source-target task correlation. We then characterize transfer optimality by analyzing the internal representations of two networks trained from scratch on the source and the target task through multiple established similarity measures.

Inducing bias is simpler than you think

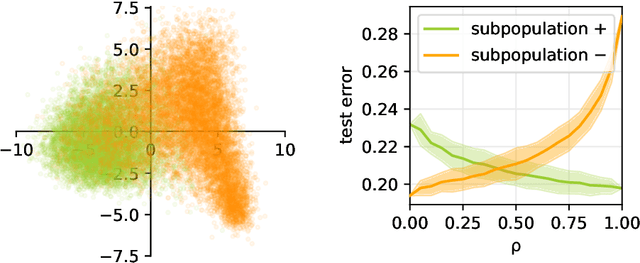
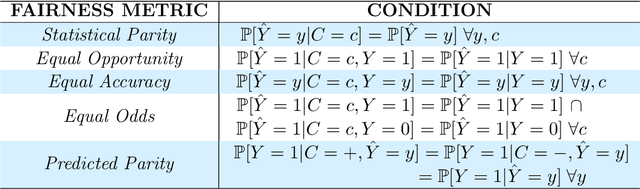
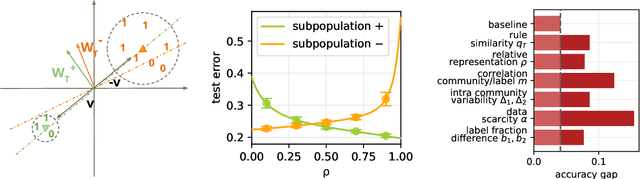
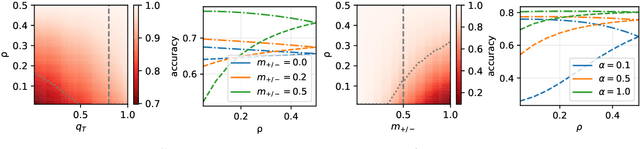
Machine learning may be oblivious to human bias but it is not immune to its perpetuation. Marginalisation and iniquitous group representation are often traceable in the very data used for training, and may be reflected or even enhanced by the learning models. To counter this, some of the model accuracy can be traded off for a secondary objective that helps prevent a specific type of bias. Multiple notions of fairness have been proposed to this end but recent studies show that some fairness criteria often stand in mutual competition. In the present work, we introduce a solvable high-dimensional model of data imbalance, where parametric control over the many bias-inducing factors allows for an extensive exploration of the bias inheritance mechanism. Through the tools of statistical physics, we analytically characterise the typical behaviour of learning models trained in our synthetic framework and find similar unfairness behaviours as those observed on more realistic data. However, we also identify a positive transfer effect between the different subpopulations within the data. This suggests that mixing data with different statistical properties could be helpful, provided the learning model is made aware of this structure. Finally, we analyse the issue of bias mitigation: by reweighing the various terms in the training loss, we indirectly minimise standard unfairness metrics and highlight their incompatibilities. Leveraging the insights on positive transfer, we also propose a theory-informed mitigation strategy, based on the introduction of coupled learning models. By allowing each model to specialise on a different community within the data, we find that multiple fairness criteria and high accuracy can be achieved simultaneously.

Maslow's Hammer for Catastrophic Forgetting: Node Re-Use vs Node Activation

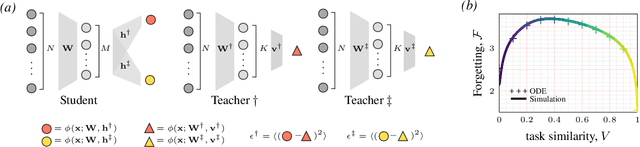
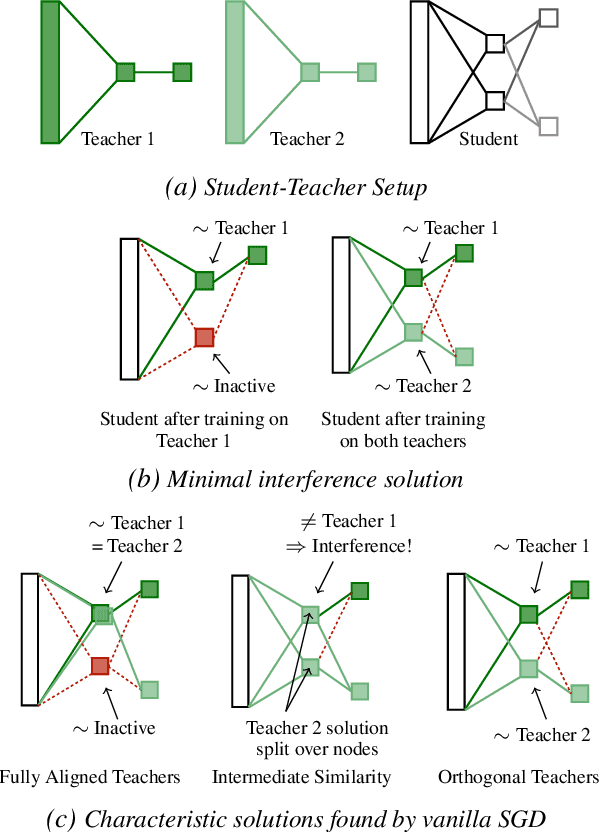
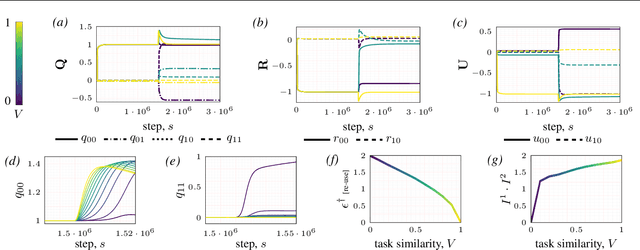
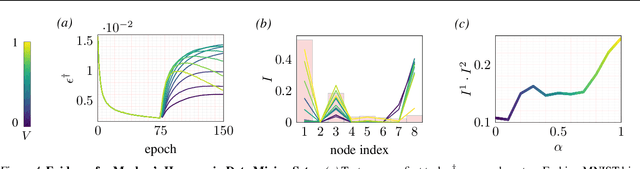
Continual learning - learning new tasks in sequence while maintaining performance on old tasks - remains particularly challenging for artificial neural networks. Surprisingly, the amount of forgetting does not increase with the dissimilarity between the learned tasks, but appears to be worst in an intermediate similarity regime. In this paper we theoretically analyse both a synthetic teacher-student framework and a real data setup to provide an explanation of this phenomenon that we name Maslow's hammer hypothesis. Our analysis reveals the presence of a trade-off between node activation and node re-use that results in worst forgetting in the intermediate regime. Using this understanding we reinterpret popular algorithmic interventions for catastrophic interference in terms of this trade-off, and identify the regimes in which they are most effective.

An Analytical Theory of Curriculum Learning in Teacher-Student Networks

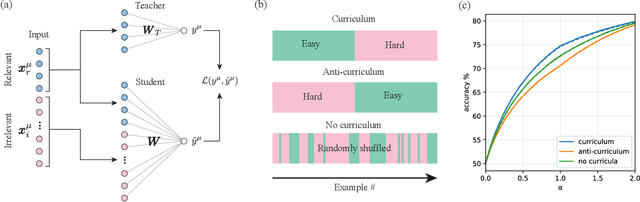
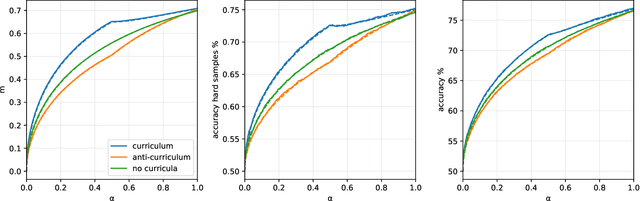
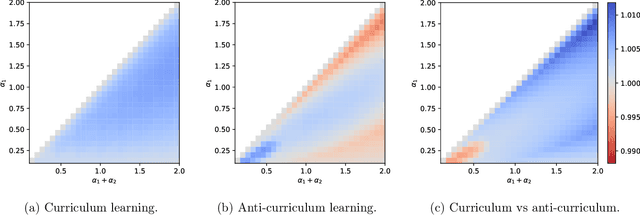
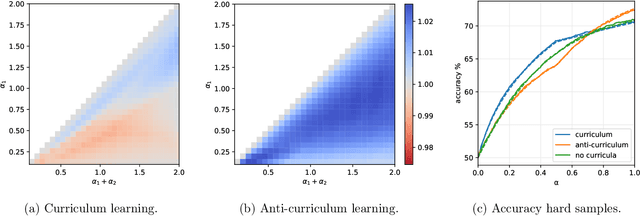
In humans and animals, curriculum learning -- presenting data in a curated order - is critical to rapid learning and effective pedagogy. Yet in machine learning, curricula are not widely used and empirically often yield only moderate benefits. This stark difference in the importance of curriculum raises a fundamental theoretical question: when and why does curriculum learning help? In this work, we analyse a prototypical neural network model of curriculum learning in the high-dimensional limit, employing statistical physics methods. Curricula could in principle change both the learning speed and asymptotic performance of a model. To study the former, we provide an exact description of the online learning setting, confirming the long-standing experimental observation that curricula can modestly speed up learning. To study the latter, we derive performance in a batch learning setting, in which a network trains to convergence in successive phases of learning on dataset slices of varying difficulty. With standard training losses, curriculum does not provide generalisation benefit, in line with empirical observations. However, we show that by connecting different learning phases through simple Gaussian priors, curriculum can yield a large improvement in test performance. Taken together, our reduced analytical descriptions help reconcile apparently conflicting empirical results and trace regimes where curriculum learning yields the largest gains. More broadly, our results suggest that fully exploiting a curriculum may require explicit changes to the loss function at curriculum boundaries.

Probing transfer learning with a model of synthetic correlated datasets

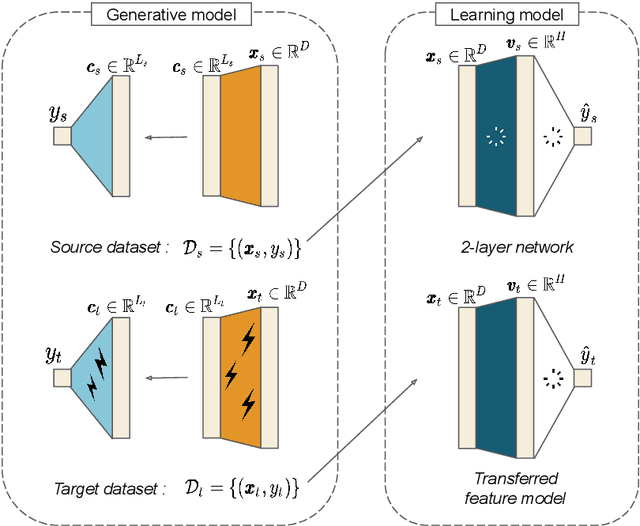
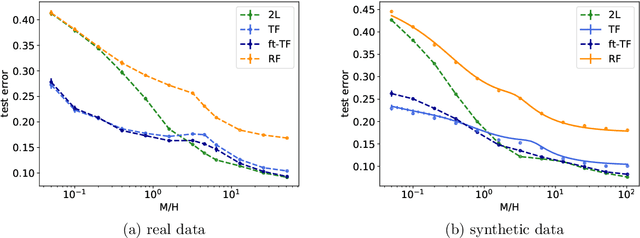
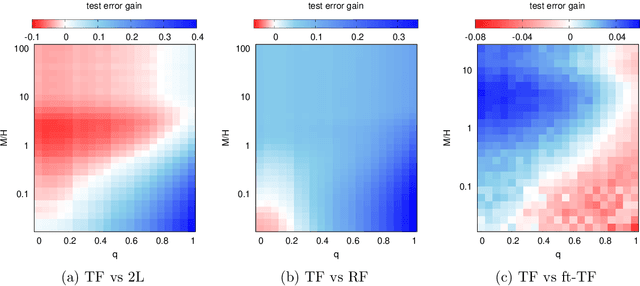
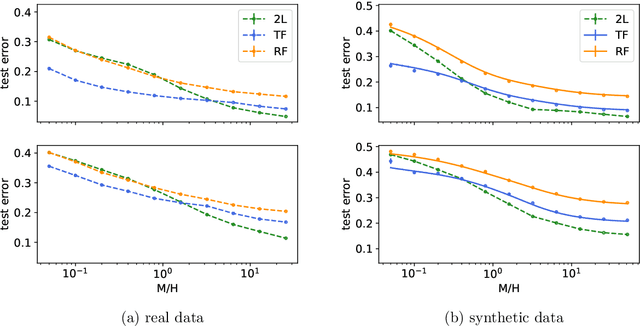
Transfer learning can significantly improve the sample efficiency of neural networks, by exploiting the relatedness between a data-scarce target task and a data-abundant source task. Despite years of successful applications, transfer learning practice often relies on ad-hoc solutions, while theoretical understanding of these procedures is still limited. In the present work, we re-think a solvable model of synthetic data as a framework for modeling correlation between data-sets. This setup allows for an analytic characterization of the generalization performance obtained when transferring the learned feature map from the source to the target task. Focusing on the problem of training two-layer networks in a binary classification setting, we show that our model can capture a range of salient features of transfer learning with real data. Moreover, by exploiting parametric control over the correlation between the two data-sets, we systematically investigate under which conditions the transfer of features is beneficial for generalization.