Bias in Motion: Theoretical Insights into the Dynamics of Bias in SGD Training

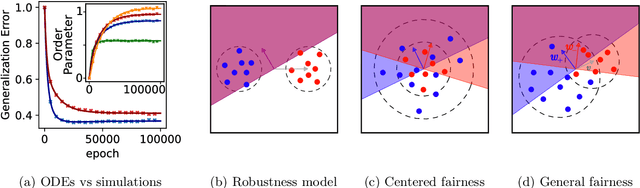
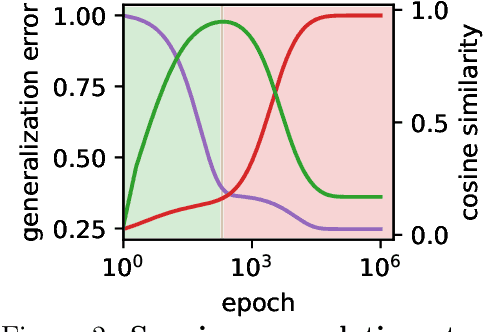
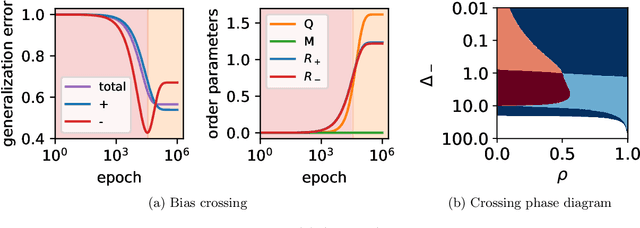
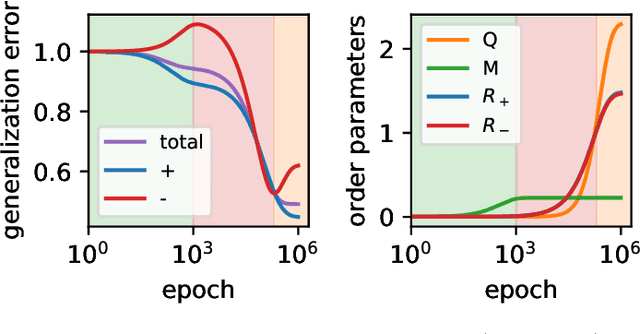
Machine learning systems often acquire biases by leveraging undesired features in the data, impacting accuracy variably across different sub-populations. Current understanding of bias formation mostly focuses on the initial and final stages of learning, leaving a gap in knowledge regarding the transient dynamics. To address this gap, this paper explores the evolution of bias in a teacher-student setup modeling different data sub-populations with a Gaussian-mixture model. We provide an analytical description of the stochastic gradient descent dynamics of a linear classifier in this setting, which we prove to be exact in high dimension. Notably, our analysis reveals how different properties of sub-populations influence bias at different timescales, showing a shifting preference of the classifier during training. Applying our findings to fairness and robustness, we delineate how and when heterogeneous data and spurious features can generate and amplify bias. We empirically validate our results in more complex scenarios by training deeper networks on synthetic and real datasets, including CIFAR10, MNIST, and CelebA.

Do Explanations Explain? Model Knows Best

It is a mystery which input features contribute to a neural network's output. Various explanation (feature attribution) methods are proposed in the literature to shed light on the problem. One peculiar observation is that these explanations (attributions) point to different features as being important. The phenomenon raises the question, which explanation to trust? We propose a framework for evaluating the explanations using the neural network model itself. The framework leverages the network to generate input features that impose a particular behavior on the output. Using the generated features, we devise controlled experimental setups to evaluate whether an explanation method conforms to an axiom. Thus we propose an empirical framework for axiomatic evaluation of explanation methods. We evaluate well-known and promising explanation solutions using the proposed framework. The framework provides a toolset to reveal properties and drawbacks within existing and future explanation solutions.

Towards Deep Learning Models Resistant to Large Perturbations

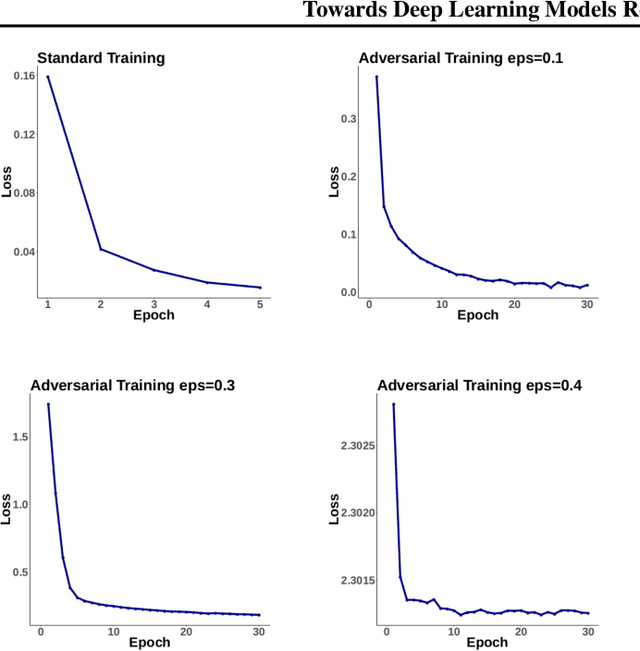
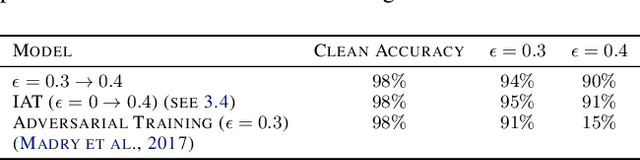
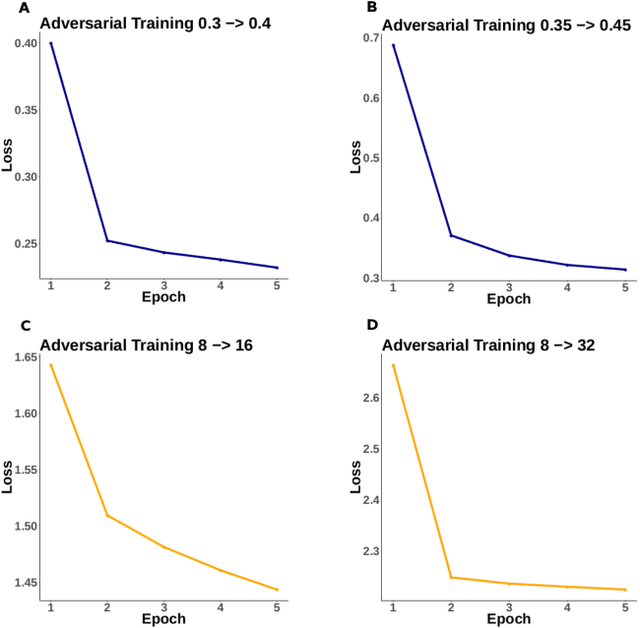
Adversarial robustness has proven to be a required property of machine learning algorithms. A key and often overlooked aspect of this problem is to try to make the adversarial noise magnitude as large as possible to enhance the benefits of the model robustness. We show that the well-established algorithm called "adversarial training" fails to train a deep neural network given a large, but reasonable, perturbation magnitude. In this paper, we propose a simple yet effective initialization of the network weights that makes learning on higher levels of noise possible. We next evaluate this idea rigorously on MNIST ($\epsilon$ up to $\approx 0.40$) and CIFAR10 ($\epsilon$ up to $\approx 32/255$) datasets assuming the $\ell_{\infty}$ attack model. Additionally, in order to establish the limits of $\epsilon$ in which the learning is feasible, we study the optimal robust classifier assuming full access to the joint data and label distribution. Then, we provide some theoretical results on the adversarial accuracy for a simple multi-dimensional Bernoulli distribution, which yields some insights on the range of feasible perturbations for the MNIST dataset.