BayesPrompt: human readable prompts that make sense

Reconstructing prompts that can elicit a desired answer or behaviour in an LLM is an open and important research topic. Optimisation methods which aim at minimising the perplexity of a given answer, however, consistently yield so-called pseudoprompts, unintelligible strings of tokens which can lack human interpretability. We argue that this is a consequence of the ill-posedness of the prompt optimisation task. By reframing the task as a Bayesian posterior inference over prompts, we propose an efficient algorithm to sample prompts which are both efficient (in terms of perplexity) and human readable. We compare our approach with state of the art alternatives showing on a real data set a marked improvement over a range of metrics.

Texture Representations in Deep Vision Models: Comparing CNNs, Vision Transformers, and Human Perception

In computational vision science, Convolutional Neural Networks (CNNs) have emerged as a popular model of biological vision because of the alignment they can exhibit with neural and behavioral data in humans and animals. However, it remains unclear to what extent this alignment persists for visual tasks that extend beyond the canonical object recognition paradigm based on well defined semantic content. In this study, we diverge from the common object-centric view by focusing on another aspect of vision: texture perception. We consider textures of different complexity generated with three different algorithms from the same source images. Using a rank-based statistic, we quantify the information encoded in the internal representations of a CNN and three Vision Transformers (ViTs), and we compare the similarity of these representations to those inferred from human psychophysics data. We find that the representation of textures is aligned in different ViTs, but not between the ViTs and the CNN; that ViTs form similar representations for textures of different complexity; that human performance in recognizing textures can be better predicted from ViTs representations rather than CNN representations. Taken together, these results suggest that ViTs may capture more faithfully than CNNs how texture patterns are visually processed by humans, and that the representations of texture stimuli in computational models may be driven by the network architecture.

Signal-to-Noise Ratio and Sample Size Govern Representational Alignment in Neural Networks

Neural networks are known to develop latent representations that are $aligned$, namely structurally similar across networks trained with different architectures, training protocols, or training datasets. We study this phenomenon in a controlled setting, where we train an ensemble of networks on regression and classification tasks using training sets perturbed by independent realizations of a noise process. We show that the signal-to-noise ratio (SNR) and the training sample size influence the alignment in qualitatively similar ways in networks trained on real-world datasets and in an extremely simple $linear$ network with a single hidden layer, for which the alignment can be estimated analytically. Across linear and nonlinear networks, regression and classification tasks, and both synthetic and real-world data, we consistently observe that alignment varies monotonically with SNR but non-monotonically with training sample size. In particular, the alignment is minimized near the interpolation threshold, and a stronger alignment does not necessarily correspond to better generalization error. These findings reveal a non-trivial dependence of alignment on data quality and quantity, decoupled from generalization performance.

Differential syntactic and semantic encoding in LLMs

We study how syntactic and semantic information is encoded in inner layer representations of Large Language Models (LLMs), focusing on the very large DeepSeek-V3. We find that, by averaging hidden-representation vectors of sentences sharing syntactic structure or meaning, we obtain vectors that capture a significant proportion of the syntactic and semantic information contained in the representations. In particular, subtracting these syntactic and semantic ``centroids'' from sentence vectors strongly affects their similarity with syntactically and semantically matched sentences, respectively, suggesting that syntax and semantics are, at least partially, linearly encoded. We also find that the cross-layer encoding profiles of syntax and semantics are different, and that the two signals can to some extent be decoupled, suggesting differential encoding of these two types of linguistic information in LLM representations.

An approach to identify the most semantically informative deep representations of text and images

Deep neural networks are known to develop similar representations for semantically related data, even when they belong to different domains, such as an image and its description, or the same text in different languages. We present a method for quantitatively investigating this phenomenon by measuring the relative information content of the representations of semantically related data and probing how it is encoded into multiple tokens of large language models (LLMs) and vision transformers. Looking first at how LLMs process pairs of translated sentences, we identify inner ``semantic'' layers containing the most language-transferable information. We find moreover that, on these layers, a larger LLM (DeepSeek-V3) extracts significantly more general information than a smaller one (Llama3.1-8B). Semantic information is spread across many tokens and it is characterized by long-distance correlations between tokens and by a causal left-to-right (i.e., past-future) asymmetry. We also identify layers encoding semantic information within visual transformers. We show that caption representations in the semantic layers of LLMs predict visual representations of the corresponding images. We observe significant and model-dependent information asymmetries between image and text representations.

Detecting Localized Density Anomalies in Multivariate Data via Coin-Flip Statistics

Detecting localized density differences in multivariate data is a crucial task in computational science. Such anomalies can indicate a critical system failure, lead to a groundbreaking scientific discovery, or reveal unexpected changes in data distribution. We introduce EagleEye, an anomaly detection method to compare two multivariate datasets with the aim of identifying local density anomalies, namely over- or under-densities affecting only localised regions of the feature space. Anomalies are detected by modelling, for each point, the ordered sequence of its neighbours' membership label as a coin-flipping process and monitoring deviations from the expected behaviour of such process. A unique advantage of our method is its ability to provide an accurate, entirely unsupervised estimate of the local signal purity. We demonstrate its effectiveness through experiments on both synthetic and real-world datasets. In synthetic data, EagleEye accurately detects anomalies in multiple dimensions even when they affect a tiny fraction of the data. When applied to a challenging resonant anomaly detection benchmark task in simulated Large Hadron Collider data, EagleEye successfully identifies particle decay events present in just 0.3% of the dataset. In global temperature data, EagleEye uncovers previously unidentified, geographically localised changes in temperature fields that occurred in the most recent years. Thanks to its key advantages of conceptual simplicity, computational efficiency, trivial parallelisation, and scalability, EagleEye is widely applicable across many fields.

Unsupervised detection of semantic correlations in big data

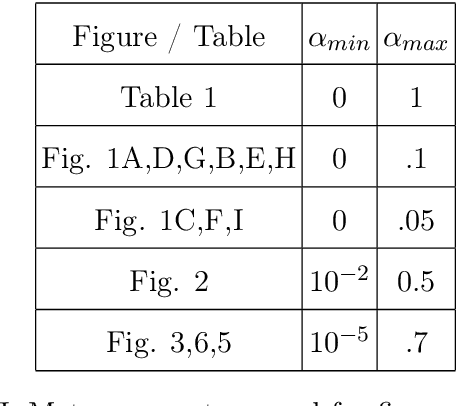
In real-world data, information is stored in extremely large feature vectors. These variables are typically correlated due to complex interactions involving many features simultaneously. Such correlations qualitatively correspond to semantic roles and are naturally recognized by both the human brain and artificial neural networks. This recognition enables, for instance, the prediction of missing parts of an image or text based on their context. We present a method to detect these correlations in high-dimensional data represented as binary numbers. We estimate the binary intrinsic dimension of a dataset, which quantifies the minimum number of independent coordinates needed to describe the data, and is therefore a proxy of semantic complexity. The proposed algorithm is largely insensitive to the so-called curse of dimensionality, and can therefore be used in big data analysis. We test this approach identifying phase transitions in model magnetic systems and we then apply it to the detection of semantic correlations of images and text inside deep neural networks.

Automatic feature selection and weighting using Differentiable Information Imbalance

Feature selection is a common process in many applications, but it is accompanied by uncertainties such as: What is the optimal dimensionality of an interpretable, reduced feature space to retain a maximum amount of information? How to account for different units of measure in features? How to weight different features according to their importance? To address these challenges, we introduce the Differentiable Information Imbalance (DII), an automatic data analysis method to rank information content between sets of features. Based on the nearest neighbors according to distances in the ground truth feature space, the method finds a low-dimensional subset of the input features, within which the pairwise distance relations are most similar to the ground truth. By employing the Differentiable Information Imbalance as a loss function, the relative feature weights of the inputs are optimized, simultaneously performing unit alignment and relative importance scaling, while preserving interpretability. Furthermore, this method can generate sparse solutions and determine the optimal size of the reduced feature space. We illustrate the usefulness of this approach on two prototypical benchmark problems: (1) Identifying a small set of collective variables capable of describing the conformational space of a biomolecule, and (2) selecting a subset of features for training a machine-learning force field. The results highlight the potential of the Differentiable Information Imbalance in addressing feature selection challenges and optimizing dimensionality in various applications. The method is implemented in the Python library DADApy.

A distributional simplicity bias in the learning dynamics of transformers

The remarkable capability of over-parameterised neural networks to generalise effectively has been explained by invoking a ``simplicity bias'': neural networks prevent overfitting by initially learning simple classifiers before progressing to more complex, non-linear functions. While simplicity biases have been described theoretically and experimentally in feed-forward networks for supervised learning, the extent to which they also explain the remarkable success of transformers trained with self-supervised techniques remains unclear. In our study, we demonstrate that transformers, trained on natural language data, also display a simplicity bias. Specifically, they sequentially learn many-body interactions among input tokens, reaching a saturation point in the prediction error for low-degree interactions while continuing to learn high-degree interactions. To conduct this analysis, we develop a procedure to generate \textit{clones} of a given natural language data set, which rigorously capture the interactions between tokens up to a specified order. This approach opens up the possibilities of studying how interactions of different orders in the data affect learning, in natural language processing and beyond.

Density Estimation via Binless Multidimensional Integration

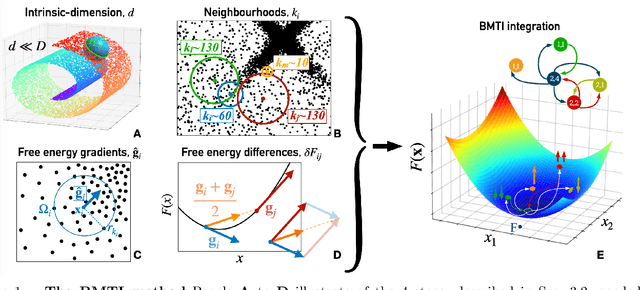
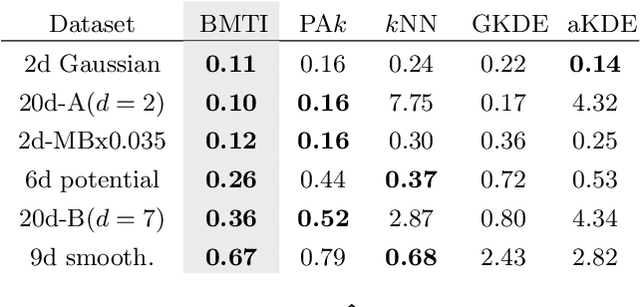
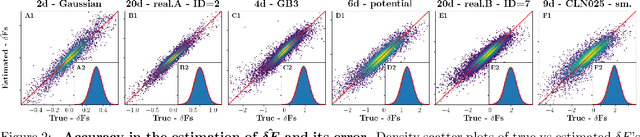
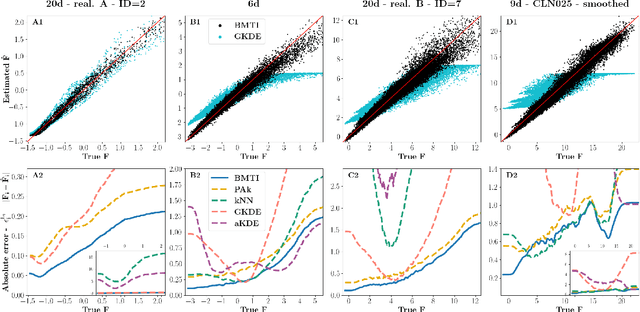
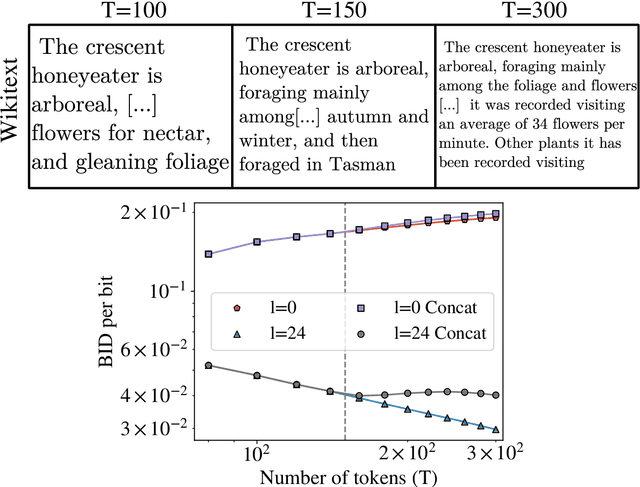
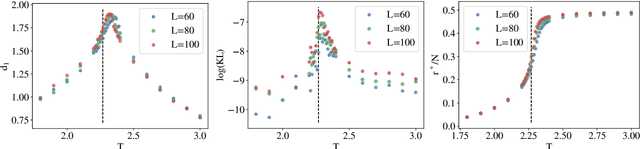
We introduce the Binless Multidimensional Thermodynamic Integration (BMTI) method for nonparametric, robust, and data-efficient density estimation. BMTI estimates the logarithm of the density by initially computing log-density differences between neighbouring data points. Subsequently, such differences are integrated, weighted by their associated uncertainties, using a maximum-likelihood formulation. This procedure can be seen as an extension to a multidimensional setting of the thermodynamic integration, a technique developed in statistical physics. The method leverages the manifold hypothesis, estimating quantities within the intrinsic data manifold without defining an explicit coordinate map. It does not rely on any binning or space partitioning, but rather on the construction of a neighbourhood graph based on an adaptive bandwidth selection procedure. BMTI mitigates the limitations commonly associated with traditional nonparametric density estimators, effectively reconstructing smooth profiles even in high-dimensional embedding spaces. The method is tested on a variety of complex synthetic high-dimensional datasets, where it is shown to outperform traditional estimators, and is benchmarked on realistic datasets from the chemical physics literature.