Detecting Localized Density Anomalies in Multivariate Data via Coin-Flip Statistics

Detecting localized density differences in multivariate data is a crucial task in computational science. Such anomalies can indicate a critical system failure, lead to a groundbreaking scientific discovery, or reveal unexpected changes in data distribution. We introduce EagleEye, an anomaly detection method to compare two multivariate datasets with the aim of identifying local density anomalies, namely over- or under-densities affecting only localised regions of the feature space. Anomalies are detected by modelling, for each point, the ordered sequence of its neighbours' membership label as a coin-flipping process and monitoring deviations from the expected behaviour of such process. A unique advantage of our method is its ability to provide an accurate, entirely unsupervised estimate of the local signal purity. We demonstrate its effectiveness through experiments on both synthetic and real-world datasets. In synthetic data, EagleEye accurately detects anomalies in multiple dimensions even when they affect a tiny fraction of the data. When applied to a challenging resonant anomaly detection benchmark task in simulated Large Hadron Collider data, EagleEye successfully identifies particle decay events present in just 0.3% of the dataset. In global temperature data, EagleEye uncovers previously unidentified, geographically localised changes in temperature fields that occurred in the most recent years. Thanks to its key advantages of conceptual simplicity, computational efficiency, trivial parallelisation, and scalability, EagleEye is widely applicable across many fields.

Cellular Automaton With CNN

Cellular automata (CA) models are widely used to simulate complex systems with emergent behaviors, but identifying hidden parameters that govern their dynamics remains a significant challenge. This study explores the use of Convolutional Neural Networks (CNN) to identify jump parameters in a two-dimensional CA model. We propose a custom CNN architecture trained on CA-generated data to classify jump parameters, which dictates the neighborhood size and movement rules of cells within the CA. Experiments were conducted across varying domain sizes (25 x 25 to 150 x 150) and CA iterations (0 to 50), demonstrating that the accuracy improves with larger domain sizes, as they provide more spatial information for parameter estimation. Interestingly, while initial CA iterations enhance the performance, increasing the number of iterations beyond a certain threshold does not significantly improve accuracy, suggesting that only specific temporal information is relevant for parameter identification. The proposed CNN achieves competitive accuracy (89.31) compared to established architectures like LeNet-5 and AlexNet, while offering significantly faster inference times, making it suitable for real-time applications. This study highlights the potential of CNNs as a powerful tool for fast and accurate parameter estimation in CA models, paving the way for their use in more complex systems and higher-dimensional domains. Future work will explore the identification of multiple hidden parameters and extend the approach to three-dimensional CA models.

Kernel-based retrieval models for hyperspectral image data optimized with Kernel Flows

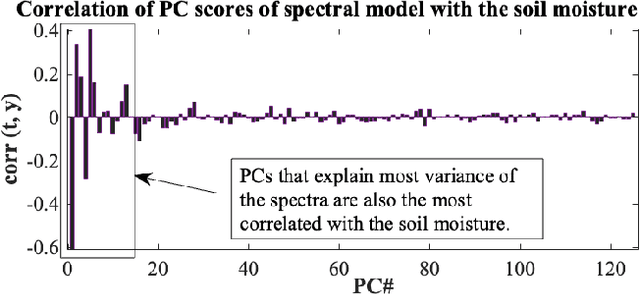
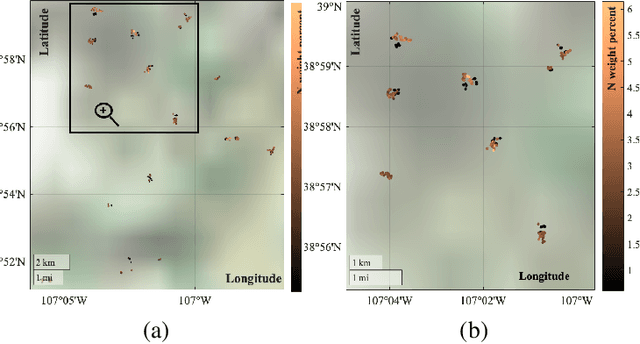
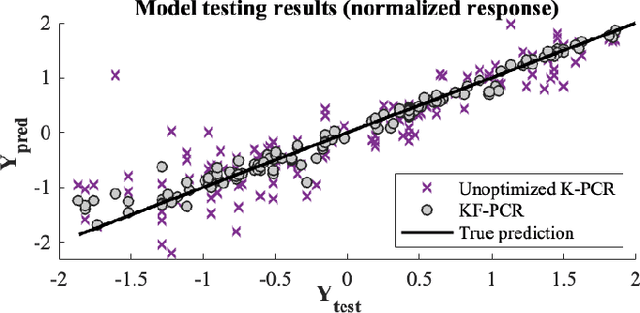
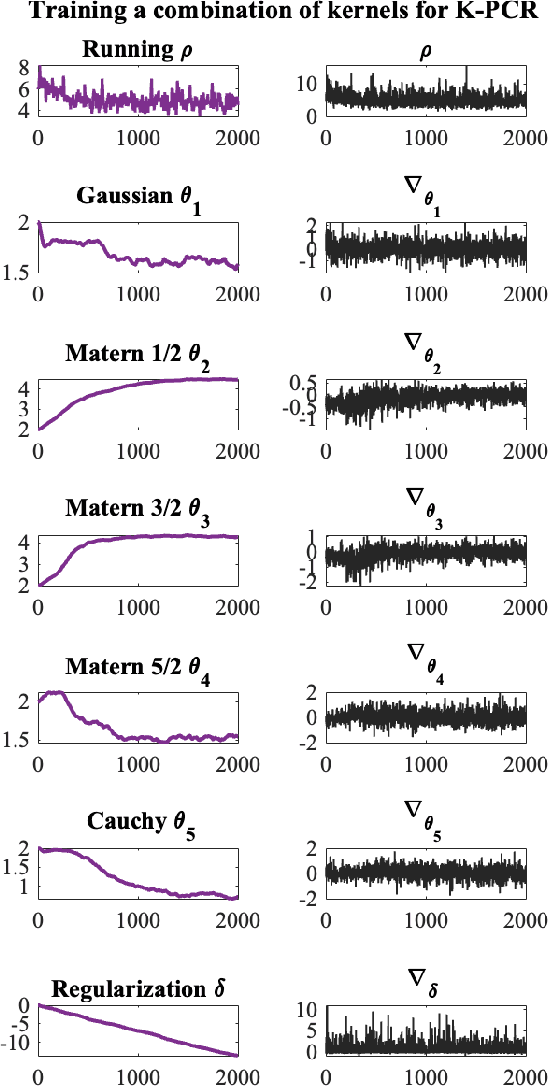
Kernel-based statistical methods are efficient, but their performance depends heavily on the selection of kernel parameters. In literature, the optimization studies on kernel-based chemometric methods is limited and often reduced to grid searching. Previously, the authors introduced Kernel Flows (KF) to learn kernel parameters for Kernel Partial Least-Squares (K-PLS) regression. KF is easy to implement and helps minimize overfitting. In cases of high collinearity between spectra and biogeophysical quantities in spectroscopy, simpler methods like Principal Component Regression (PCR) may be more suitable. In this study, we propose a new KF-type approach to optimize Kernel Principal Component Regression (K-PCR) and test it alongside KF-PLS. Both methods are benchmarked against non-linear regression techniques using two hyperspectral remote sensing datasets.

KF-PLS: Optimizing Kernel Partial Least-Squares (K-PLS) with Kernel Flows

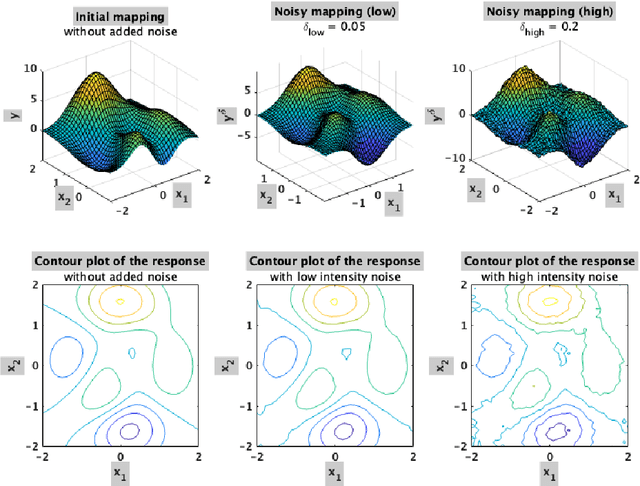
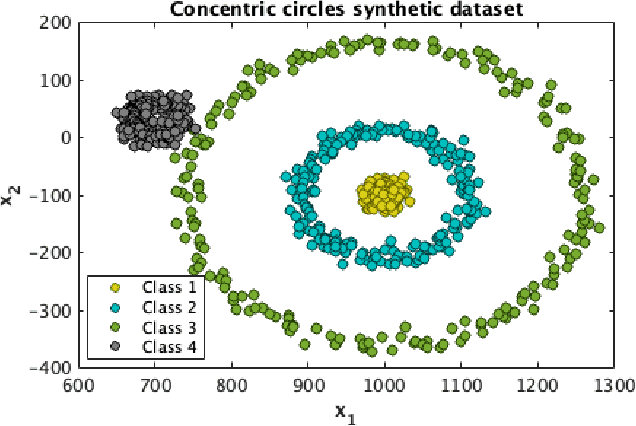
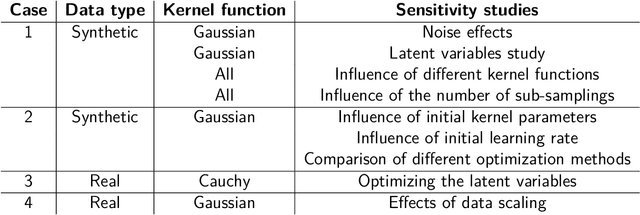
Partial Least-Squares (PLS) Regression is a widely used tool in chemometrics for performing multivariate regression. PLS is a bi-linear method that has a limited capacity of modelling non-linear relations between the predictor variables and the response. Kernel PLS (K-PLS) has been introduced for modelling non-linear predictor-response relations. In K-PLS, the input data is mapped via a kernel function to a Reproducing Kernel Hilbert space (RKH), where the dependencies between the response and the input matrix are assumed to be linear. K-PLS is performed in the RKH space between the kernel matrix and the dependent variable. Most available studies use fixed kernel parameters. Only a few studies have been conducted on optimizing the kernel parameters for K-PLS. In this article, we propose a methodology for the kernel function optimization based on Kernel Flows (KF), a technique developed for Gaussian process regression (GPR). The results are illustrated with four case studies. The case studies represent both numerical examples and real data used in classification and regression tasks. K-PLS optimized with KF, called KF-PLS in this study, is shown to yield good results in all illustrated scenarios. The paper presents cross-validation studies and hyperparameter analysis of the KF methodology when applied to K-PLS.

Reconstruction and segmentation from sparse sequential X-ray measurements of wood logs

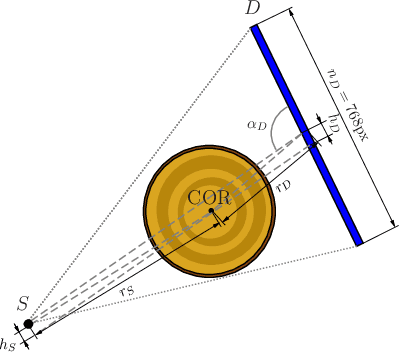
In industrial applications it is common to scan objects on a moving conveyor belt. If slice-wise 2D computed tomography (CT) measurements of the moving object are obtained we call it a sequential scanning geometry. In this case, each slice on its own does not carry sufficient information to reconstruct a useful tomographic image. Thus, here we propose the use of a Dimension reduced Kalman Filter to accumulate information between slices and allow for sufficiently accurate reconstructions for further assessment of the object. Additionally, we propose to use an unsupervised clustering approach known as Density Peak Advanced, to perform a segmentation and spot density anomalies in the internal structure of the reconstructed objects. We evaluate the method in a proof of concept study for the application of wood log scanning for the industrial sawing process, where the goal is to spot anomalies within the wood log to allow for optimal sawing patterns. Reconstruction and segmentation quality is evaluated from experimental measurement data for various scenarios of severely undersampled X-measurements. Results show clearly that an improvement of reconstruction quality can be obtained by employing the Dimension reduced Kalman Filter allowing to robustly obtain the segmented logs.

Resolving Overlapping Convex Objects in Silhouette Images by Concavity Analysis and Gaussian Process

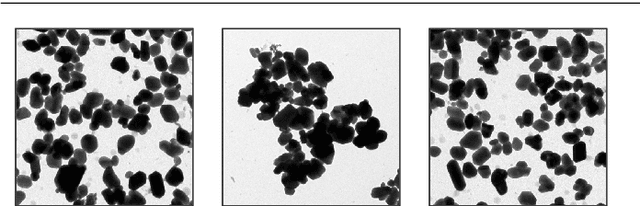
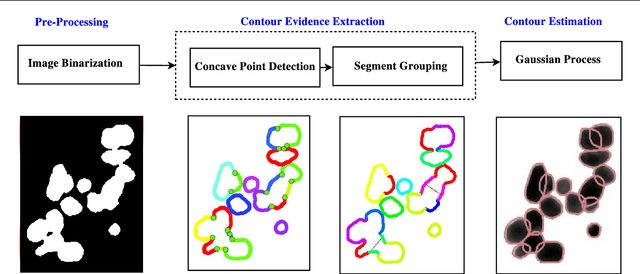
Segmentation of overlapping convex objects has various applications, for example, in nanoparticles and cell imaging. Often the segmentation method has to rely purely on edges between the background and foreground making the analyzed images essentially silhouette images. Therefore, to segment the objects, the method needs to be able to resolve the overlaps between multiple objects by utilizing prior information about the shape of the objects. This paper introduces a novel method for segmentation of clustered partially overlapping convex objects in silhouette images. The proposed method involves three main steps: pre-processing, contour evidence extraction, and contour estimation. Contour evidence extraction starts by recovering contour segments from a binarized image by detecting concave points. After this, the contour segments which belong to the same objects are grouped. The grouping is formulated as a combinatorial optimization problem and solved using the branch and bound algorithm. Finally, the full contours of the objects are estimated by a Gaussian process regression method. The experiments on a challenging dataset consisting of nanoparticles demonstrate that the proposed method outperforms three current state-of-art approaches in overlapping convex objects segmentation. The method relies only on edge information and can be applied to any segmentation problems where the objects are partially overlapping and have a convex shape.