Identifiability and amortized inference limitations in Kuramoto models

Bayesian inference is a powerful tool for parameter estimation and uncertainty quantification in dynamical systems. However, for nonlinear oscillator networks such as Kuramoto models, widely used to study synchronization phenomena in physics, biology, and engineering, inference is often computationally prohibitive due to high-dimensional state spaces and intractable likelihood functions. We present an amortized Bayesian inference approach that learns a neural approximation of the posterior from simulated phase dynamics, enabling fast, scalable inference without repeated sampling or optimization. Applied to synthetic Kuramoto networks, the method shows promising results in approximating posterior distributions and capturing uncertainty, with computational savings compared to traditional Bayesian techniques. These findings suggest that amortized inference is a practical and flexible framework for uncertainty-aware analysis of oscillator networks.

Bayesian LSTM for indoor temperature modeling

Improving energy efficiency of building heating systems is essential for reducing global energy consumption and greenhouse gas emissions. Traditional control methods in buildings rely on static heating curves based solely on outdoor temperature measurements, neglecting system state and free heat sources like solar gain. Model predictive control (MPC) not only addresses these limitations but further optimizes heating control by incorporating weather forecasts and system state predictions. However, current industrial MPC solutions often use simplified physics-inspired models, which compromise accuracy for interpretability. While purely data-driven models offer better predictive performance, they face challenges like overfitting and lack of transparency. To bridge this gap, we propose a Bayesian Long Short-Term Memory (LSTM) architecture for indoor temperature modeling. Our experiments across 100 real-world buildings demonstrate that the Bayesian LSTM outperforms an industrial physics-based model in predictive accuracy, enabling potential for improved energy efficiency and thermal comfort if deployed in heating MPC solutions. Over deterministic black-box approaches, the Bayesian framework provides additional advantages by improving generalization ability and allowing interpretation of predictions via uncertainty quantification. This work advances data-driven heating control by balancing predictive performance with the transparency and reliability required for real-world heating MPC applications.

Statistical Batch-Based Bearing Fault Detection

In the domain of rotating machinery, bearings are vulnerable to different mechanical faults, including ball, inner, and outer race faults. Various techniques can be used in condition-based monitoring, from classical signal analysis to deep learning methods. Based on the complex working conditions of rotary machines, multivariate statistical process control charts such as Hotelling's $T^2$ and Squared Prediction Error are useful for providing early warnings. However, these methods are rarely applied to condition monitoring of rotating machinery due to the univariate nature of the datasets. In the present paper, we propose a multivariate statistical process control-based fault detection method that utilizes multivariate data composed of Fourier transform features extracted for fixed-time batches. Our approach makes use of the multidimensional nature of Fourier transform characteristics, which record more detailed information about the machine's status, in an effort to enhance early defect detection and diagnosis. Experiments with varying vibration measurement locations (Fan End, Drive End), fault types (ball, inner, and outer race faults), and motor loads (0-3 horsepower) are used to validate the suggested approach. The outcomes illustrate our method's effectiveness in fault detection and point to possible broader uses in industrial maintenance.

Log-Gaussian Gamma Processes for Training Bayesian Neural Networks in Raman and CARS Spectroscopies

We propose an approach utilizing gamma-distributed random variables, coupled with log-Gaussian modeling, to generate synthetic datasets suitable for training neural networks. This addresses the challenge of limited real observations in various applications. We apply this methodology to both Raman and coherent anti-Stokes Raman scattering (CARS) spectra, using experimental spectra to estimate gamma process parameters. Parameter estimation is performed using Markov chain Monte Carlo methods, yielding a full Bayesian posterior distribution for the model which can be sampled for synthetic data generation. Additionally, we model the additive and multiplicative background functions for Raman and CARS with Gaussian processes. We train two Bayesian neural networks to estimate parameters of the gamma process which can then be used to estimate the underlying Raman spectrum and simultaneously provide uncertainty through the estimation of parameters of a probability distribution. We apply the trained Bayesian neural networks to experimental Raman spectra of phthalocyanine blue, aniline black, naphthol red, and red 264 pigments and also to experimental CARS spectra of adenosine phosphate, fructose, glucose, and sucrose. The results agree with deterministic point estimates for the underlying Raman and CARS spectral signatures.

Mixtures of Gaussian Process Experts with SMC$^2$

Gaussian processes are a key component of many flexible statistical and machine learning models. However, they exhibit cubic computational complexity and high memory constraints due to the need of inverting and storing a full covariance matrix. To circumvent this, mixtures of Gaussian process experts have been considered where data points are assigned to independent experts, reducing the complexity by allowing inference based on smaller, local covariance matrices. Moreover, mixtures of Gaussian process experts substantially enrich the model's flexibility, allowing for behaviors such as non-stationarity, heteroscedasticity, and discontinuities. In this work, we construct a novel inference approach based on nested sequential Monte Carlo samplers to simultaneously infer both the gating network and Gaussian process expert parameters. This greatly improves inference compared to importance sampling, particularly in settings when a stationary Gaussian process is inappropriate, while still being thoroughly parallelizable.

Geometry parameter estimation for sparse X-ray log imaging

We consider geometry parameter estimation in industrial sawmill fan-beam X-ray tomography. In such industrial settings, scanners do not always allow identification of the location of the source-detector pair, which creates the issue of unknown geometry. This work considers two approaches for geometry estimation. Our first approach is a calibration object correlation method in which we calculate the maximum cross-correlation between a known-sized calibration object image and its filtered backprojection reconstruction and use differential evolution as an optimiser. The second approach is projection trajectory simulation, where we use a set of known intersection points and a sequential Monte Carlo method for estimating the posterior density of the parameters. We show numerically that a large set of parameters can be used for artefact-free reconstruction. We deploy Bayesian inversion with Cauchy priors for synthetic and real sawmill data for detection of knots with a very low number of measurements and uncertain measurement geometry.

Reconstruction and segmentation from sparse sequential X-ray measurements of wood logs

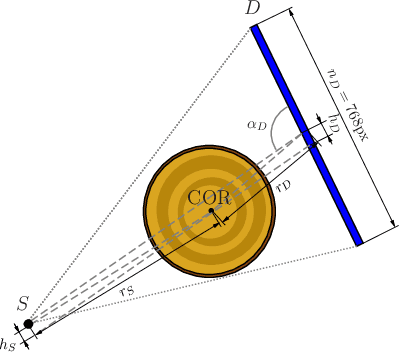
In industrial applications it is common to scan objects on a moving conveyor belt. If slice-wise 2D computed tomography (CT) measurements of the moving object are obtained we call it a sequential scanning geometry. In this case, each slice on its own does not carry sufficient information to reconstruct a useful tomographic image. Thus, here we propose the use of a Dimension reduced Kalman Filter to accumulate information between slices and allow for sufficiently accurate reconstructions for further assessment of the object. Additionally, we propose to use an unsupervised clustering approach known as Density Peak Advanced, to perform a segmentation and spot density anomalies in the internal structure of the reconstructed objects. We evaluate the method in a proof of concept study for the application of wood log scanning for the industrial sawing process, where the goal is to spot anomalies within the wood log to allow for optimal sawing patterns. Reconstruction and segmentation quality is evaluated from experimental measurement data for various scenarios of severely undersampled X-measurements. Results show clearly that an improvement of reconstruction quality can be obtained by employing the Dimension reduced Kalman Filter allowing to robustly obtain the segmented logs.

Blind hierarchical deconvolution

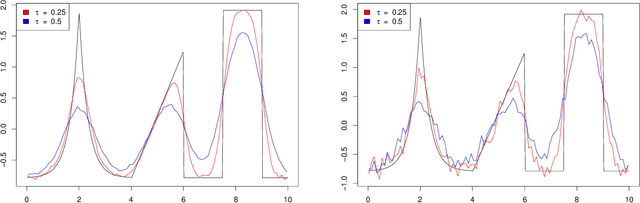
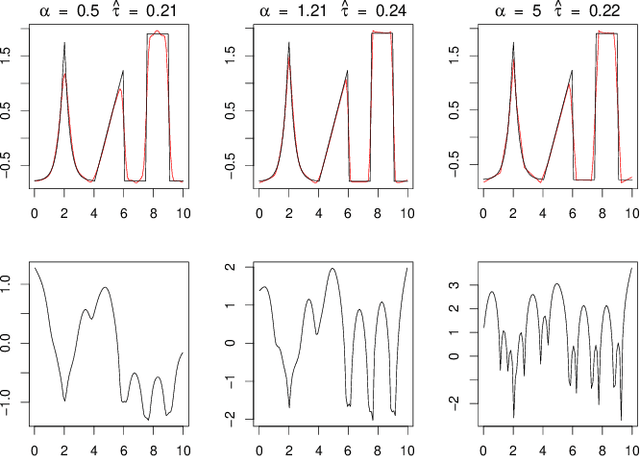
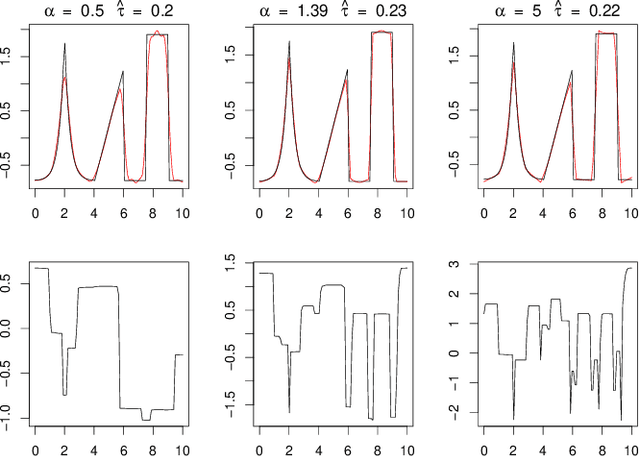
Deconvolution is a fundamental inverse problem in signal processing and the prototypical model for recovering a signal from its noisy measurement. Nevertheless, the majority of model-based inversion techniques require knowledge on the convolution kernel to recover an accurate reconstruction and additionally prior assumptions on the regularity of the signal are needed. To overcome these limitations, we parametrise the convolution kernel and prior length-scales, which are then jointly estimated in the inversion procedure. The proposed framework of blind hierarchical deconvolution enables accurate reconstructions of functions with varying regularity and unknown kernel size and can be solved efficiently with an empirical Bayes two-step procedure, where hyperparameters are first estimated by optimisation and other unknowns then by an analytical formula.