Blind hierarchical deconvolution
Paper and Code
Jul 22, 2020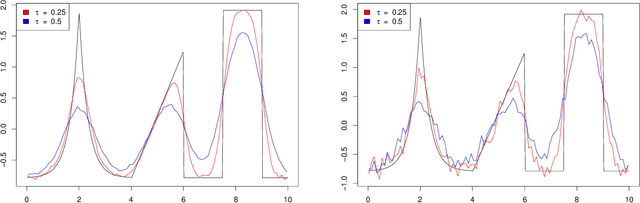

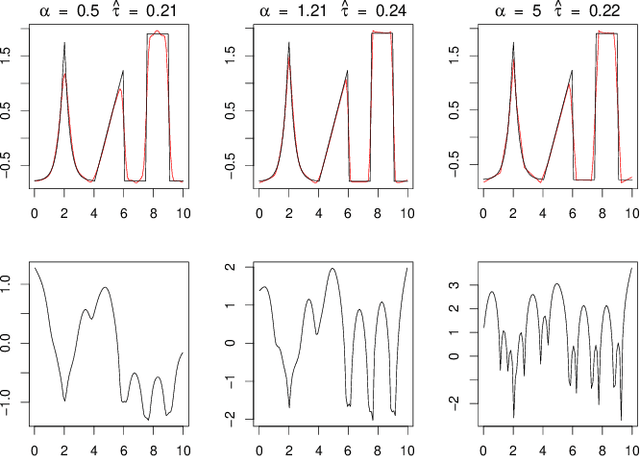
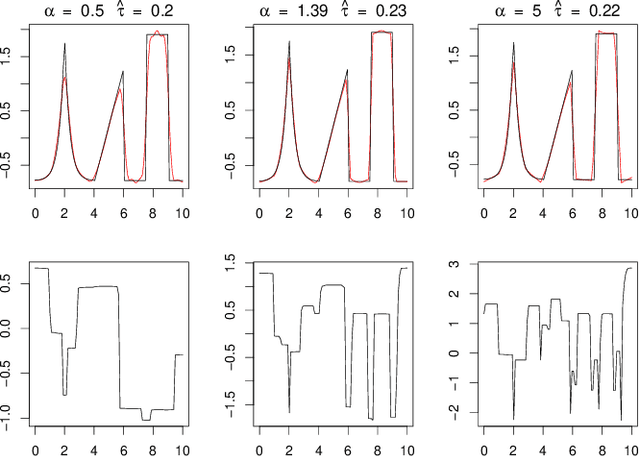
Deconvolution is a fundamental inverse problem in signal processing and the prototypical model for recovering a signal from its noisy measurement. Nevertheless, the majority of model-based inversion techniques require knowledge on the convolution kernel to recover an accurate reconstruction and additionally prior assumptions on the regularity of the signal are needed. To overcome these limitations, we parametrise the convolution kernel and prior length-scales, which are then jointly estimated in the inversion procedure. The proposed framework of blind hierarchical deconvolution enables accurate reconstructions of functions with varying regularity and unknown kernel size and can be solved efficiently with an empirical Bayes two-step procedure, where hyperparameters are first estimated by optimisation and other unknowns then by an analytical formula.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge