Device Detection and Channel Estimation in MTC with Correlated Activity Pattern

This paper provides a solution for the activity detection and channel estimation problem in grant-free access with correlated device activity patterns. In particular, we consider a machine-type communications (MTC) network operating in event-triggered traffic mode, where the devices are distributed over clusters with an activity behaviour that exhibits both intra-cluster and inner-cluster sparsity patterns. Furthermore, to model the network's intra-cluster and inner-cluster sparsity, we propose a structured sparsity-inducing spike-and-slab prior which provides a flexible approach to encode the prior information about the correlated sparse activity pattern. Furthermore, we drive a Bayesian inference scheme based on the expectation propagation (EP) framework to solve the JUICE problem. Numerical results highlight the significant gains obtained by the proposed structured sparsity-inducing spike-and-slab prior in terms of both user identification accuracy and channel estimation performance.

Hierarchical MTC User Activity Detection and Channel Estimation with Unknown Spatial Covariance

This paper addresses the joint user identification and channel estimation (JUICE) problem in machine-type communications under the practical spatially correlated channels model with unknown covariance matrices. Furthermore, we consider an MTC network with hierarchical user activity patterns following an event-triggered traffic mode. Therein the users are distributed over clusters with a structured sporadic activity behaviour that exhibits both cluster-level and intra-cluster sparsity patterns. To solve the JUICE problem, we first leverage the concept of strong priors and propose a hierarchical-sparsity-inducing spike-and-slab prior to model the structured sparse activity pattern. Subsequently, we derive a Bayesian inference scheme by coupling the expectation propagation (EP) algorithm with the expectation maximization (EM) framework. Second, we reformulate the JUICE as a maximum a posteriori (MAP) estimation problem and propose a computationally-efficient solution based on the alternating direction method of multipliers (ADMM). More precisely, we relax the strong spike-and-slab prior with a cluster-sparsity-promoting prior based on the long-sum penalty. We then derive an ADMM algorithm that solves the MAP problem through a sequence of closed-form updates. Numerical results highlight the significant performance significant gains obtained by the proposed algorithms, as well as their robustness against various assumptions on the users sparse activity behaviour.

Neural Network Kalman filtering for 3D object tracking from linear array ultrasound data

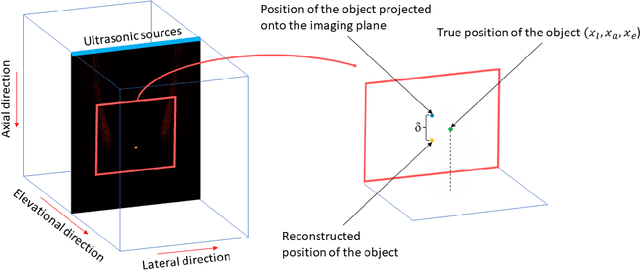
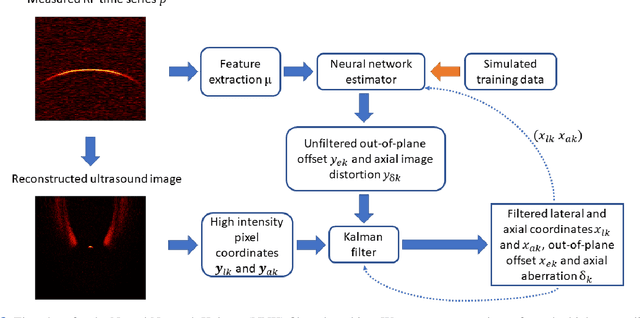
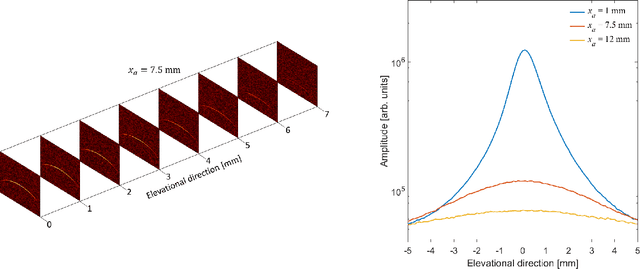
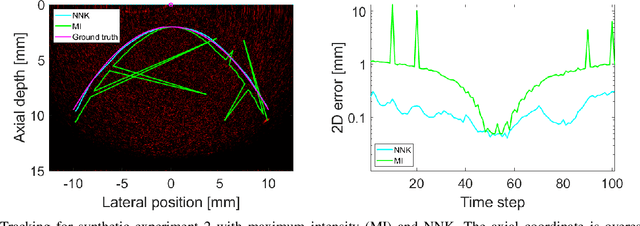
Many interventional surgical procedures rely on medical imaging to visualise and track instruments. Such imaging methods not only need to be real-time capable, but also provide accurate and robust positional information. In ultrasound applications, typically only two-dimensional data from a linear array are available, and as such obtaining accurate positional estimation in three dimensions is non-trivial. In this work, we first train a neural network, using realistic synthetic training data, to estimate the out-of-plane offset of an object with the associated axial aberration in the reconstructed ultrasound image. The obtained estimate is then combined with a Kalman filtering approach that utilises positioning estimates obtained in previous time-frames to improve localisation robustness and reduce the impact of measurement noise. The accuracy of the proposed method is evaluated using simulations, and its practical applicability is demonstrated on experimental data obtained using a novel optical ultrasound imaging setup. Accurate and robust positional information is provided in real-time. Axial and lateral coordinates for out-of-plane objects are estimated with a mean error of 0.1mm for simulated data and a mean error of 0.2mm for experimental data. Three-dimensional localisation is most accurate for elevational distances larger than 1mm, with a maximum distance of 5mm considered for a 25mm aperture.

Blind hierarchical deconvolution

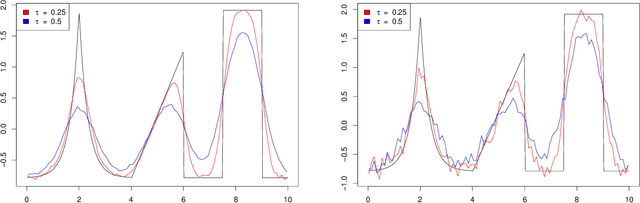
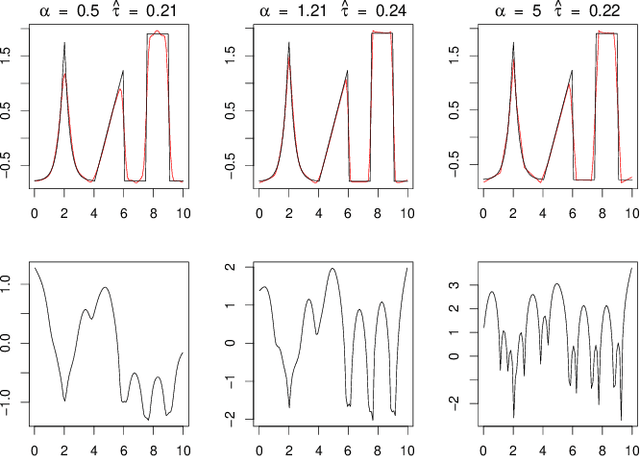
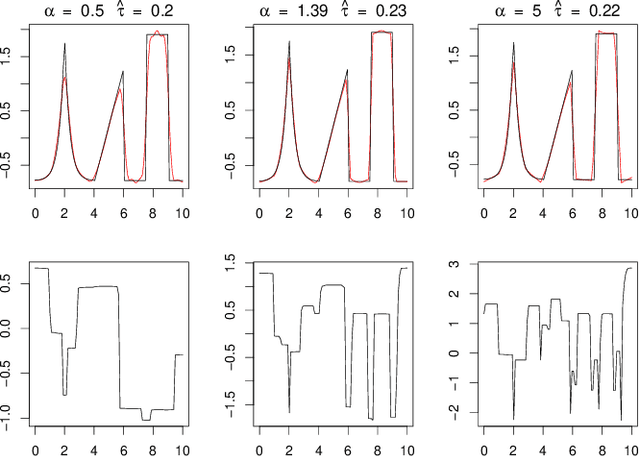
Deconvolution is a fundamental inverse problem in signal processing and the prototypical model for recovering a signal from its noisy measurement. Nevertheless, the majority of model-based inversion techniques require knowledge on the convolution kernel to recover an accurate reconstruction and additionally prior assumptions on the regularity of the signal are needed. To overcome these limitations, we parametrise the convolution kernel and prior length-scales, which are then jointly estimated in the inversion procedure. The proposed framework of blind hierarchical deconvolution enables accurate reconstructions of functions with varying regularity and unknown kernel size and can be solved efficiently with an empirical Bayes two-step procedure, where hyperparameters are first estimated by optimisation and other unknowns then by an analytical formula.