Nonlinear Sparse Bayesian Learning Methods with Application to Massive MIMO Channel Estimation with Hardware Impairments

Accurate channel estimation is critical for realizing the performance gains of massive multiple-input multiple-output (MIMO) systems. Traditional approaches to channel estimation typically assume ideal receiver hardware and linear signal models. However, practical receivers suffer from impairments such as nonlinearities in the low-noise amplifiers and quantization errors, which invalidate standard model assumptions and degrade the estimation accuracy. In this work, we propose a nonlinear channel estimation framework that models the distortion function arising from hardware impairments using Gaussian process (GP) regression while leveraging the inherent sparsity of massive MIMO channels. First, we form a GP-based surrogate of the distortion function, employing pseudo-inputs to reduce the computational complexity. Then, we integrate the GP-based surrogate of the distortion function into newly developed enhanced sparse Bayesian learning (SBL) methods, enabling distortion-aware sparse channel estimation. Specifically, we propose two nonlinear SBL methods based on distinct optimization objectives, each offering a different trade-off between estimation accuracy and computational complexity. Numerical results demonstrate significant gains over the Bussgang linear minimum mean squared error estimator and linear SBL, particularly under strong distortion and at high signal-to-noise ratio.

Enhanced Sparse Bayesian Learning Methods with Application to Massive MIMO Channel Estimation

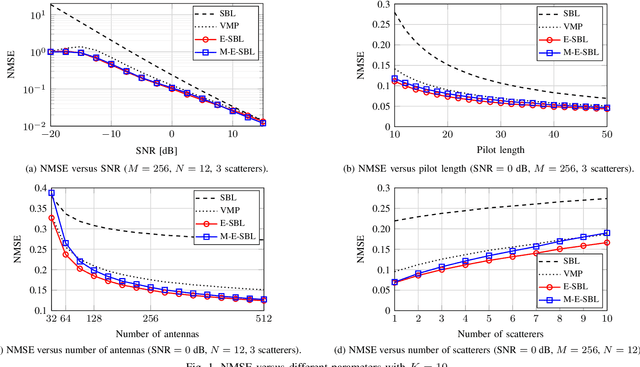
We consider the problem of sparse channel estimation in massive multiple-input multiple-output systems. In this context, we propose an enhanced version of the sparse Bayesian learning (SBL) framework, referred to as enhanced SBL (E-SBL), which is based on a reparameterization of the original SBL model. Specifically, we introduce a scale vector that brings extra flexibility to the model, which is estimated along with the other unknowns. Moreover, we introduce a variant of E-SBL, referred to as modified E-SBL (M-E-SBL), which is based on a computationally more efficient parameter estimation. We compare the proposed E-SBL and M-E-SBL with the baseline SBL and with a method based on variational message passing (VMP) in terms of computational complexity and performance. Numerical results show that the proposed E-SBL and M-E-SBL outperform the baseline SBL and VMP in terms of mean squared error of the channel estimation in all the considered scenarios. Furthermore, we show that M-E-SBL produces results comparable with E-SBL with considerably cheaper computations.

Neural Network Kalman filtering for 3D object tracking from linear array ultrasound data

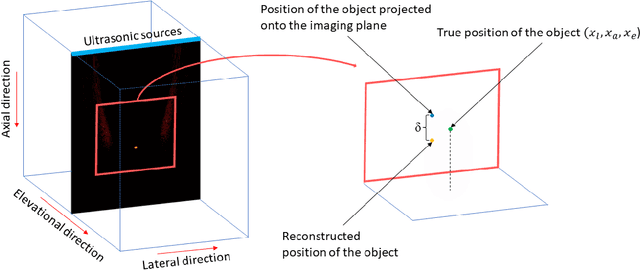
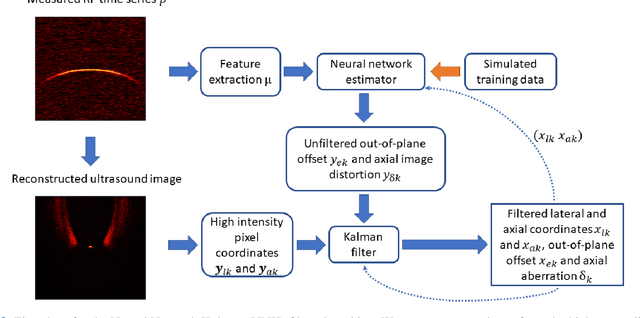
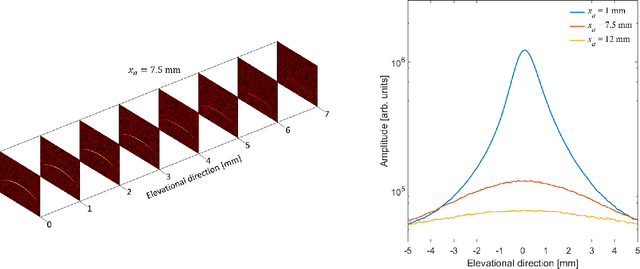
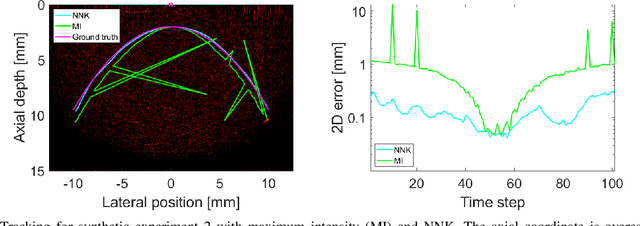
Many interventional surgical procedures rely on medical imaging to visualise and track instruments. Such imaging methods not only need to be real-time capable, but also provide accurate and robust positional information. In ultrasound applications, typically only two-dimensional data from a linear array are available, and as such obtaining accurate positional estimation in three dimensions is non-trivial. In this work, we first train a neural network, using realistic synthetic training data, to estimate the out-of-plane offset of an object with the associated axial aberration in the reconstructed ultrasound image. The obtained estimate is then combined with a Kalman filtering approach that utilises positioning estimates obtained in previous time-frames to improve localisation robustness and reduce the impact of measurement noise. The accuracy of the proposed method is evaluated using simulations, and its practical applicability is demonstrated on experimental data obtained using a novel optical ultrasound imaging setup. Accurate and robust positional information is provided in real-time. Axial and lateral coordinates for out-of-plane objects are estimated with a mean error of 0.1mm for simulated data and a mean error of 0.2mm for experimental data. Three-dimensional localisation is most accurate for elevational distances larger than 1mm, with a maximum distance of 5mm considered for a 25mm aperture.

Blind hierarchical deconvolution

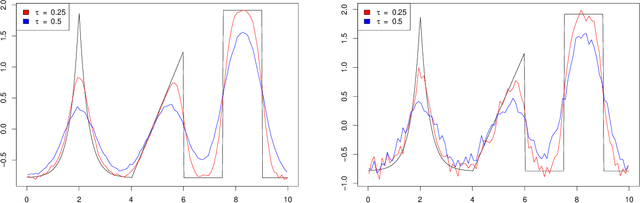
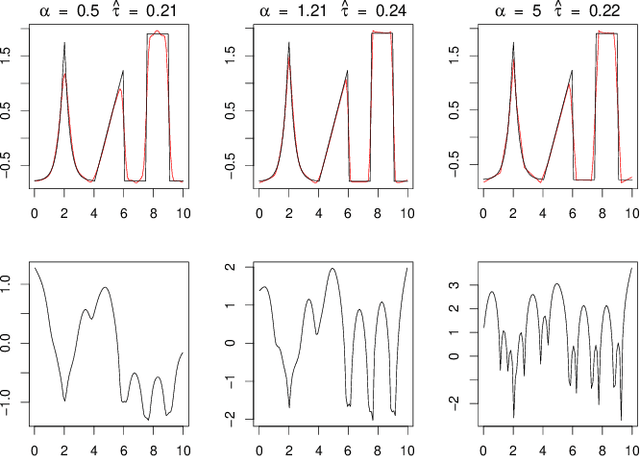
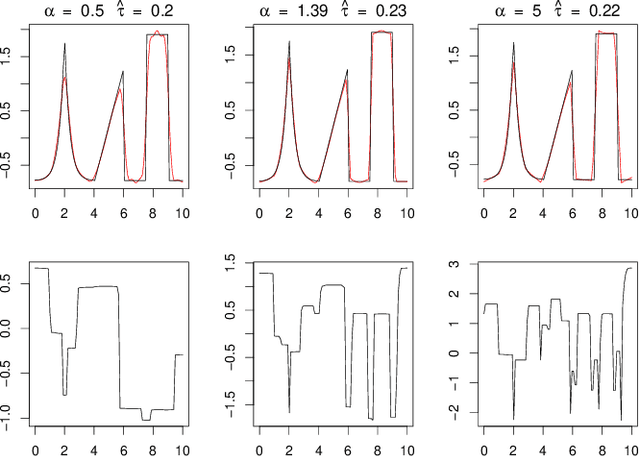
Deconvolution is a fundamental inverse problem in signal processing and the prototypical model for recovering a signal from its noisy measurement. Nevertheless, the majority of model-based inversion techniques require knowledge on the convolution kernel to recover an accurate reconstruction and additionally prior assumptions on the regularity of the signal are needed. To overcome these limitations, we parametrise the convolution kernel and prior length-scales, which are then jointly estimated in the inversion procedure. The proposed framework of blind hierarchical deconvolution enables accurate reconstructions of functions with varying regularity and unknown kernel size and can be solved efficiently with an empirical Bayes two-step procedure, where hyperparameters are first estimated by optimisation and other unknowns then by an analytical formula.