Variational Bayesian Bow tie Neural Networks with Shrinkage

Despite the dominant role of deep models in machine learning, limitations persist, including overconfident predictions, susceptibility to adversarial attacks, and underestimation of variability in predictions. The Bayesian paradigm provides a natural framework to overcome such issues and has become the gold standard for uncertainty estimation with deep models, also providing improved accuracy and a framework for tuning critical hyperparameters. However, exact Bayesian inference is challenging, typically involving variational algorithms that impose strong independence and distributional assumptions. Moreover, existing methods are sensitive to the architectural choice of the network. We address these issues by constructing a relaxed version of the standard feed-forward rectified neural network, and employing Polya-Gamma data augmentation tricks to render a conditionally linear and Gaussian model. Additionally, we use sparsity-promoting priors on the weights of the neural network for data-driven architectural design. To approximate the posterior, we derive a variational inference algorithm that avoids distributional assumptions and independence across layers and is a faster alternative to the usual Markov Chain Monte Carlo schemes.

Leveraging variational autoencoders for multiple data imputation

Missing data persists as a major barrier to data analysis across numerous applications. Recently, deep generative models have been used for imputation of missing data, motivated by their ability to capture highly non-linear and complex relationships in the data. In this work, we investigate the ability of deep models, namely variational autoencoders (VAEs), to account for uncertainty in missing data through multiple imputation strategies. We find that VAEs provide poor empirical coverage of missing data, with underestimation and overconfident imputations, particularly for more extreme missing data values. To overcome this, we employ $\beta$-VAEs, which viewed from a generalized Bayes framework, provide robustness to model misspecification. Assigning a good value of $\beta$ is critical for uncertainty calibration and we demonstrate how this can be achieved using cross-validation. In downstream tasks, we show how multiple imputation with $\beta$-VAEs can avoid false discoveries that arise as artefacts of imputation.

Mixtures of Gaussian Process Experts with SMC$^2$

Gaussian processes are a key component of many flexible statistical and machine learning models. However, they exhibit cubic computational complexity and high memory constraints due to the need of inverting and storing a full covariance matrix. To circumvent this, mixtures of Gaussian process experts have been considered where data points are assigned to independent experts, reducing the complexity by allowing inference based on smaller, local covariance matrices. Moreover, mixtures of Gaussian process experts substantially enrich the model's flexibility, allowing for behaviors such as non-stationarity, heteroscedasticity, and discontinuities. In this work, we construct a novel inference approach based on nested sequential Monte Carlo samplers to simultaneously infer both the gating network and Gaussian process expert parameters. This greatly improves inference compared to importance sampling, particularly in settings when a stationary Gaussian process is inappropriate, while still being thoroughly parallelizable.

Machine learning in the social and health sciences

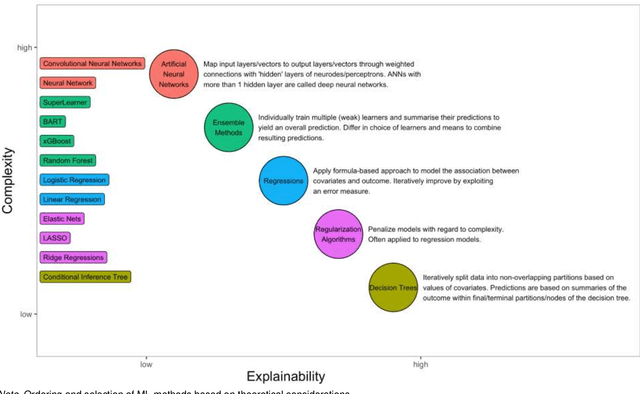
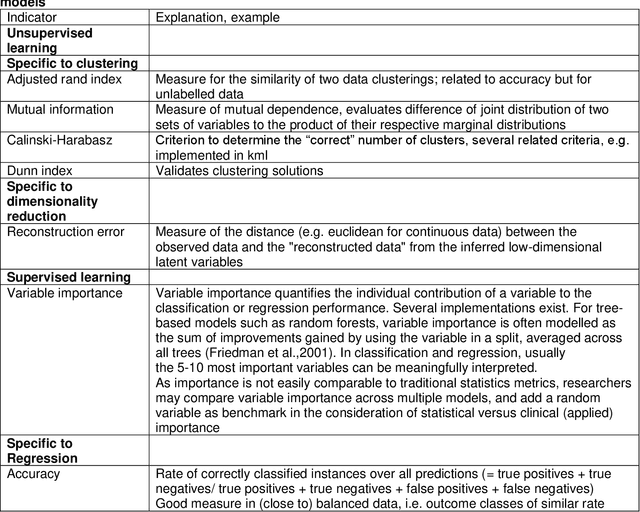
The uptake of machine learning (ML) approaches in the social and health sciences has been rather slow, and research using ML for social and health research questions remains fragmented. This may be due to the separate development of research in the computational/data versus social and health sciences as well as a lack of accessible overviews and adequate training in ML techniques for non data science researchers. This paper provides a meta-mapping of research questions in the social and health sciences to appropriate ML approaches, by incorporating the necessary requirements to statistical analysis in these disciplines. We map the established classification into description, prediction, and causal inference to common research goals, such as estimating prevalence of adverse health or social outcomes, predicting the risk of an event, and identifying risk factors or causes of adverse outcomes. This meta-mapping aims at overcoming disciplinary barriers and starting a fluid dialogue between researchers from the social and health sciences and methodologically trained researchers. Such mapping may also help to fully exploit the benefits of ML while considering domain-specific aspects relevant to the social and health sciences, and hopefully contribute to the acceleration of the uptake of ML applications to advance both basic and applied social and health sciences research.

On MCMC for variationally sparse Gaussian processes: A pseudo-marginal approach

Gaussian processes (GPs) are frequently used in machine learning and statistics to construct powerful models. However, when employing GPs in practice, important considerations must be made, regarding the high computational burden, approximation of the posterior, choice of the covariance function and inference of its hyperparmeters. To address these issues, Hensman et al. (2015) combine variationally sparse GPs with Markov chain Monte Carlo (MCMC) to derive a scalable, flexible and general framework for GP models. Nevertheless, the resulting approach requires intractable likelihood evaluations for many observation models. To bypass this problem, we propose a pseudo-marginal (PM) scheme that offers asymptotically exact inference as well as computational gains through doubly stochastic estimators for the intractable likelihood and large datasets. In complex models, the advantages of the PM scheme are particularly evident, and we demonstrate this on a two-level GP regression model with a nonparametric covariance function to capture non-stationarity.

Ultra-fast Deep Mixtures of Gaussian Process Experts

Mixtures of experts have become an indispensable tool for flexible modelling in a supervised learning context, and sparse Gaussian processes (GP) have shown promise as a leading candidate for the experts in such models. In the present article, we propose to design the gating network for selecting the experts from such mixtures of sparse GPs using a deep neural network (DNN). This combination provides a flexible, robust, and efficient model which is able to significantly outperform competing models. We furthermore consider efficient approaches to computing maximum a posteriori (MAP) estimators of these models by iteratively maximizing the distribution of experts given allocations and allocations given experts. We also show that a recently introduced method called Cluster-Classify-Regress (CCR) is capable of providing a good approximation of the optimal solution extremely quickly. This approximation can then be further refined with the iterative algorithm.

Enriched Mixtures of Gaussian Process Experts

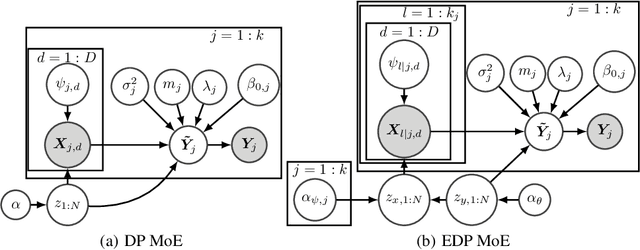
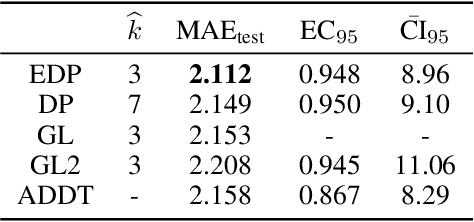
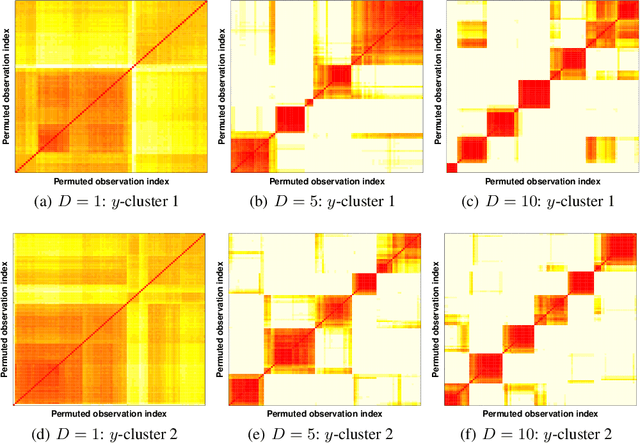
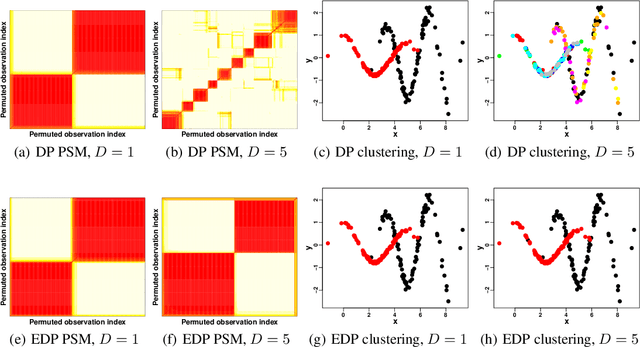
Mixtures of experts probabilistically divide the input space into regions, where the assumptions of each expert, or conditional model, need only hold locally. Combined with Gaussian process (GP) experts, this results in a powerful and highly flexible model. We focus on alternative mixtures of GP experts, which model the joint distribution of the inputs and targets explicitly. We highlight issues of this approach in multi-dimensional input spaces, namely, poor scalability and the need for an unnecessarily large number of experts, degrading the predictive performance and increasing uncertainty. We construct a novel model to address these issues through a nested partitioning scheme that automatically infers the number of components at both levels. Multiple response types are accommodated through a generalised GP framework, while multiple input types are included through a factorised exponential family structure. We show the effectiveness of our approach in estimating a parsimonious probabilistic description of both synthetic data of increasing dimension and an Alzheimer's challenge dataset.

Pseudo-marginal Bayesian inference for supervised Gaussian process latent variable models

We introduce a Bayesian framework for inference with a supervised version of the Gaussian process latent variable model. The framework overcomes the high correlations between latent variables and hyperparameters by using an unbiased pseudo estimate for the marginal likelihood that approximately integrates over the latent variables. This is used to construct a Markov Chain to explore the posterior of the hyperparameters. We demonstrate the procedure on simulated and real examples, showing its ability to capture uncertainty and multimodality of the hyperparameters and improved uncertainty quantification in predictions when compared with variational inference.