Additive Gaussian Processes Revisited

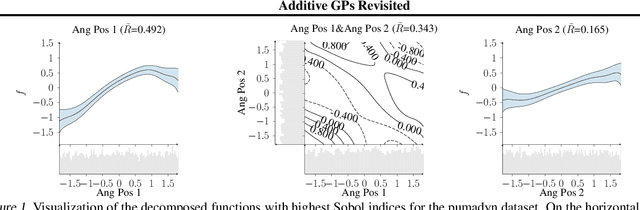
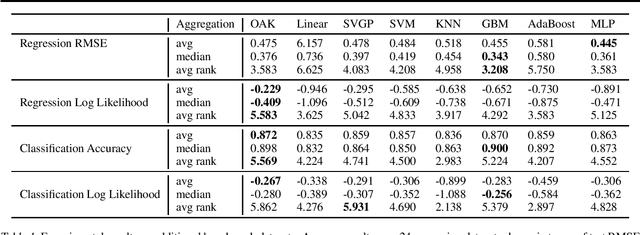
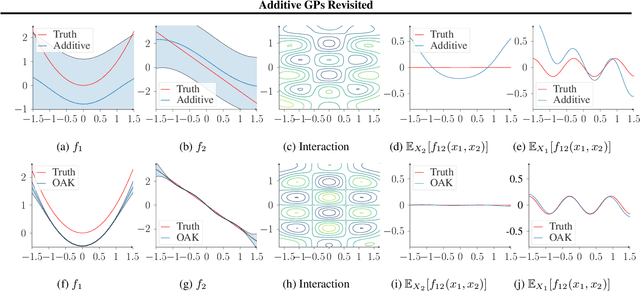
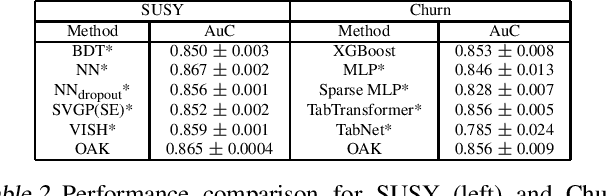
Gaussian Process (GP) models are a class of flexible non-parametric models that have rich representational power. By using a Gaussian process with additive structure, complex responses can be modelled whilst retaining interpretability. Previous work showed that additive Gaussian process models require high-dimensional interaction terms. We propose the orthogonal additive kernel (OAK), which imposes an orthogonality constraint on the additive functions, enabling an identifiable, low-dimensional representation of the functional relationship. We connect the OAK kernel to functional ANOVA decomposition, and show improved convergence rates for sparse computation methods. With only a small number of additive low-dimensional terms, we demonstrate the OAK model achieves similar or better predictive performance compared to black-box models, while retaining interpretability.

The Minecraft Kernel: Modelling correlated Gaussian Processes in the Fourier domain

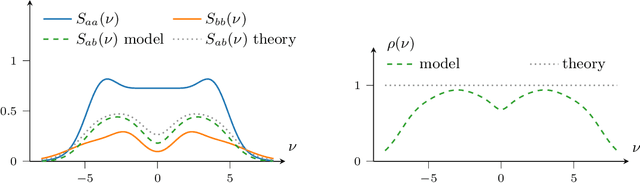
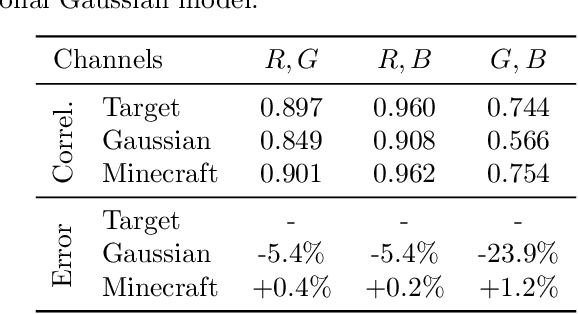
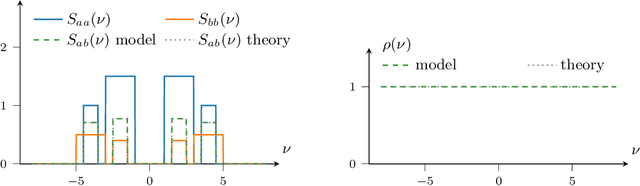
In the univariate setting, using the kernel spectral representation is an appealing approach for generating stationary covariance functions. However, performing the same task for multiple-output Gaussian processes is substantially more challenging. We demonstrate that current approaches to modelling cross-covariances with a spectral mixture kernel possess a critical blind spot. For a given pair of processes, the cross-covariance is not reproducible across the full range of permitted correlations, aside from the special case where their spectral densities are of identical shape. We present a solution to this issue by replacing the conventional Gaussian components of a spectral mixture with block components of finite bandwidth (i.e. rectangular step functions). The proposed family of kernel represents the first multi-output generalisation of the spectral mixture kernel that can approximate any stationary multi-output kernel to arbitrary precision.

Enriched Mixtures of Gaussian Process Experts

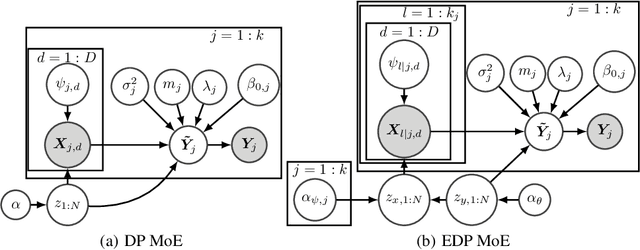
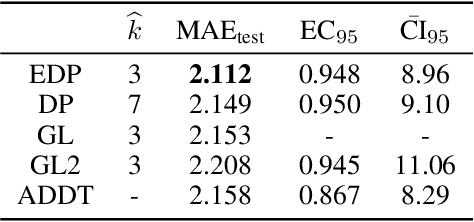
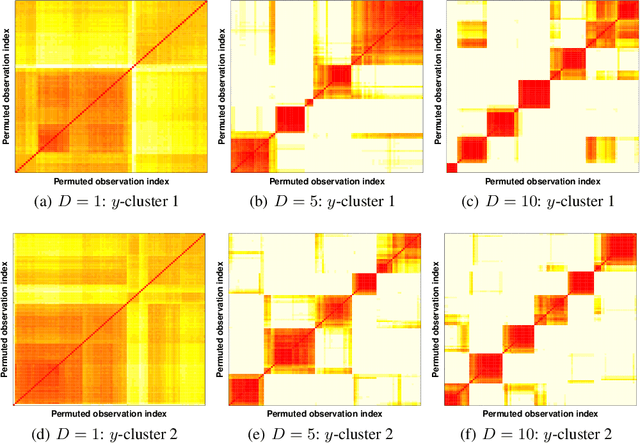
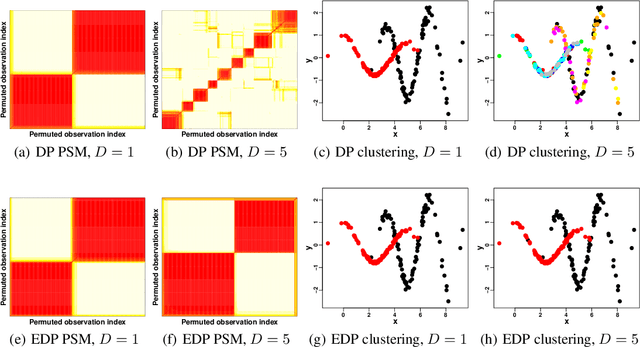
Mixtures of experts probabilistically divide the input space into regions, where the assumptions of each expert, or conditional model, need only hold locally. Combined with Gaussian process (GP) experts, this results in a powerful and highly flexible model. We focus on alternative mixtures of GP experts, which model the joint distribution of the inputs and targets explicitly. We highlight issues of this approach in multi-dimensional input spaces, namely, poor scalability and the need for an unnecessarily large number of experts, degrading the predictive performance and increasing uncertainty. We construct a novel model to address these issues through a nested partitioning scheme that automatically infers the number of components at both levels. Multiple response types are accommodated through a generalised GP framework, while multiple input types are included through a factorised exponential family structure. We show the effectiveness of our approach in estimating a parsimonious probabilistic description of both synthetic data of increasing dimension and an Alzheimer's challenge dataset.

Adaptive Sensor Placement for Continuous Spaces

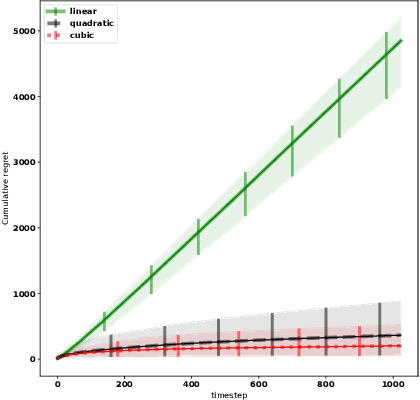
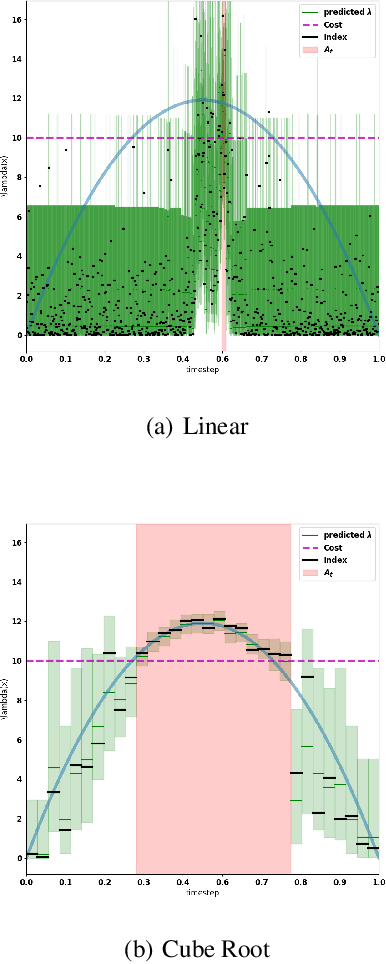
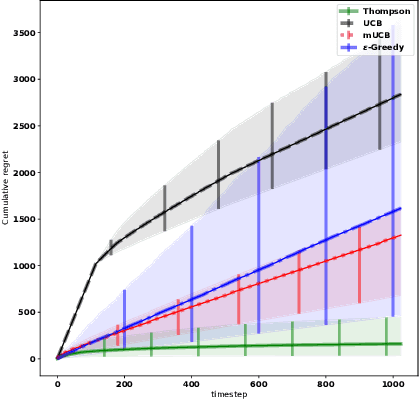
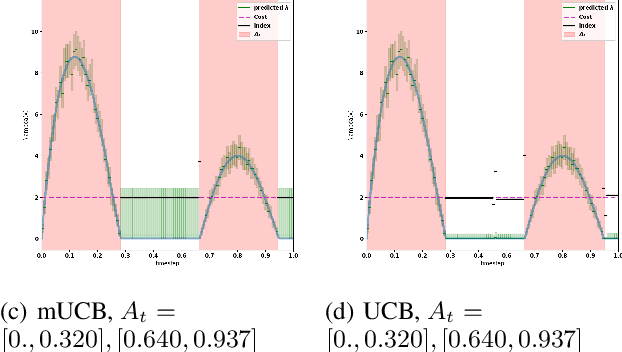
We consider the problem of adaptively placing sensors along an interval to detect stochastically-generated events. We present a new formulation of the problem as a continuum-armed bandit problem with feedback in the form of partial observations of realisations of an inhomogeneous Poisson process. We design a solution method by combining Thompson sampling with nonparametric inference via increasingly granular Bayesian histograms and derive an $\tilde{O}(T^{2/3})$ bound on the Bayesian regret in $T$ rounds. This is coupled with the design of an efficent optimisation approach to select actions in polynomial time. In simulations we demonstrate our approach to have substantially lower and less variable regret than competitor algorithms.

Decision Variance in Online Learning

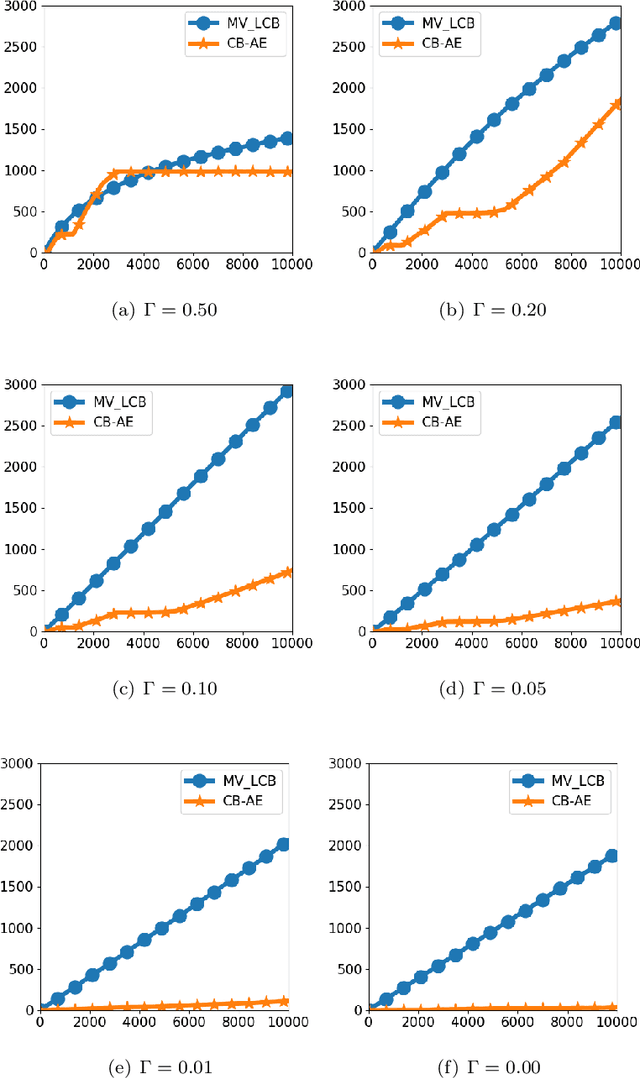
Online learning has classically focused on the expected behaviour of learning policies. Recently, risk-averse online learning has gained much attention. In this paper, a risk-averse multi-armed bandit problem where the performance of policies is measured based on the mean-variance of the rewards is studied. The variance of the rewards depends on the variance of the underlying processes as well as the variance of the player's decisions. The performance of two existing policies is analyzed and new fundamental limitations on risk-averse learning is established. In particular, it is shown that although an $\mathcal{O}(\log T)$ distribution-dependent regret in time $T$ is achievable (similar to the risk-neutral setting), the worst-case (i.e. minimax) regret is lower bounded by $\Omega(T)$ (in contrast to the $\Omega(\sqrt{T})$ lower bound in the risk-neutral setting). The lower bound results are even stronger in the sense that they are proven for the case of online learning with full feedback.

GPflow: A Gaussian process library using TensorFlow

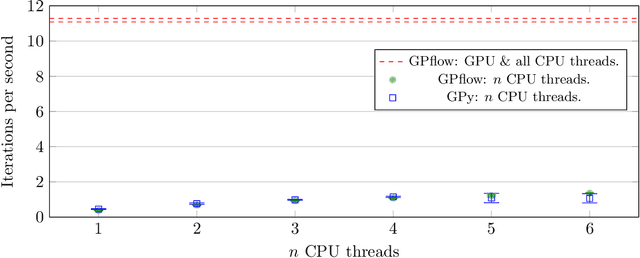
GPflow is a Gaussian process library that uses TensorFlow for its core computations and Python for its front end. The distinguishing features of GPflow are that it uses variational inference as the primary approximation method, provides concise code through the use of automatic differentiation, has been engineered with a particular emphasis on software testing and is able to exploit GPU hardware.

Simple approximate MAP Inference for Dirichlet processes

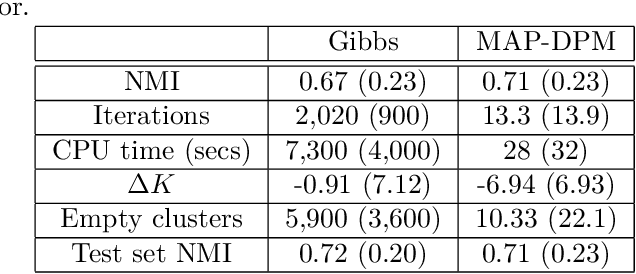
The Dirichlet process mixture (DPM) is a ubiquitous, flexible Bayesian nonparametric statistical model. However, full probabilistic inference in this model is analytically intractable, so that computationally intensive techniques such as Gibb's sampling are required. As a result, DPM-based methods, which have considerable potential, are restricted to applications in which computational resources and time for inference is plentiful. For example, they would not be practical for digital signal processing on embedded hardware, where computational resources are at a serious premium. Here, we develop simplified yet statistically rigorous approximate maximum a-posteriori (MAP) inference algorithms for DPMs. This algorithm is as simple as K-means clustering, performs in experiments as well as Gibb's sampling, while requiring only a fraction of the computational effort. Unlike related small variance asymptotics, our algorithm is non-degenerate and so inherits the "rich get richer" property of the Dirichlet process. It also retains a non-degenerate closed-form likelihood which enables standard tools such as cross-validation to be used. This is a well-posed approximation to the MAP solution of the probabilistic DPM model.

Gaussian Process Quantile Regression using Expectation Propagation

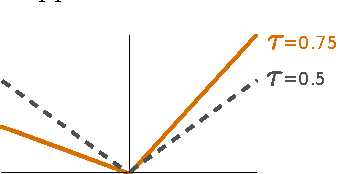
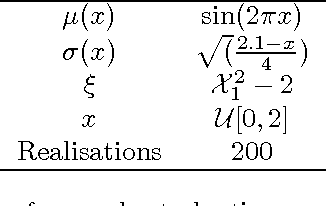
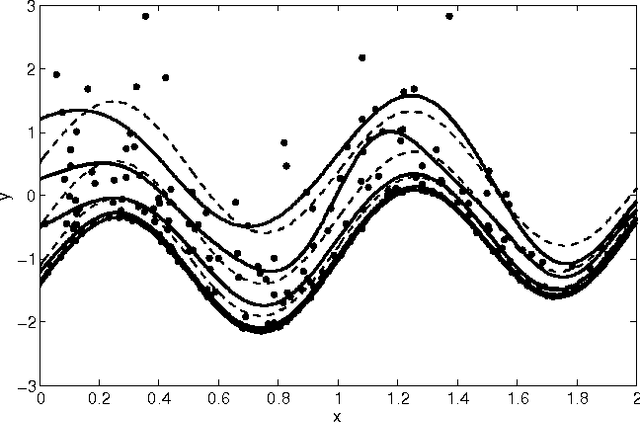
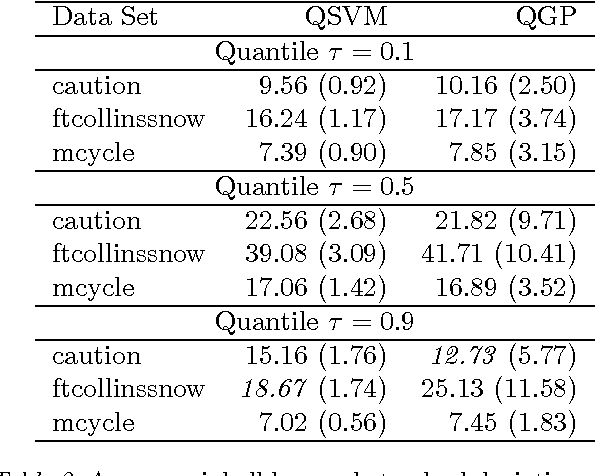
Direct quantile regression involves estimating a given quantile of a response variable as a function of input variables. We present a new framework for direct quantile regression where a Gaussian process model is learned, minimising the expected tilted loss function. The integration required in learning is not analytically tractable so to speed up the learning we employ the Expectation Propagation algorithm. We describe how this work relates to other quantile regression methods and apply the method on both synthetic and real data sets. The method is shown to be competitive with state of the art methods whilst allowing for the leverage of the full Gaussian process probabilistic framework.