Neural Diffusion Processes

Gaussian processes provide an elegant framework for specifying prior and posterior distributions over functions. They are, however, also computationally expensive, and limited by the expressivity of their covariance function. We propose Neural Diffusion Processes (NDPs), a novel approach based upon diffusion models, that learn to sample from distributions over functions. Using a novel attention block, we can incorporate properties of stochastic processes, such as exchangeability, directly into the NDP's architecture. We empirically show that NDPs are able to capture functional distributions that are close to the true Bayesian posterior of a Gaussian process. This enables a variety of downstream tasks, including hyperparameter marginalisation and Bayesian optimisation.

Validating Gaussian Process Models with Simulation-Based Calibration

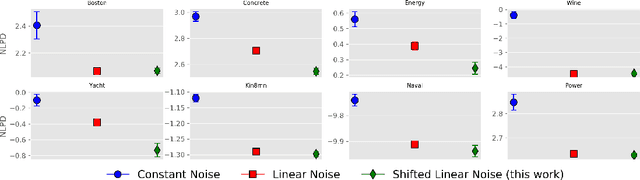
Gaussian process priors are a popular choice for Bayesian analysis of regression problems. However, the implementation of these models can be complex, and ensuring that the implementation is correct can be challenging. In this paper we introduce Gaussian process simulation-based calibration, a procedure for validating the implementation of Gaussian process models and demonstrate the efficacy of this procedure in identifying a bug in existing code. We also present a novel application of this procedure to identify when marginalisation of the model hyperparameters is necessary.

Kernel Identification Through Transformers

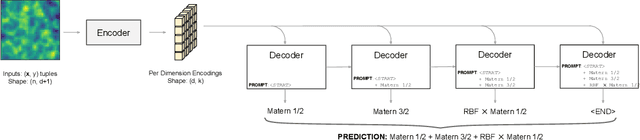
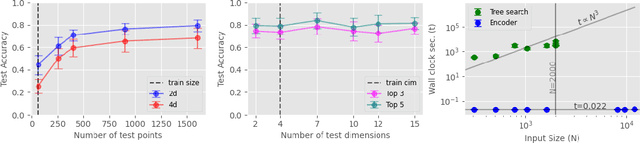
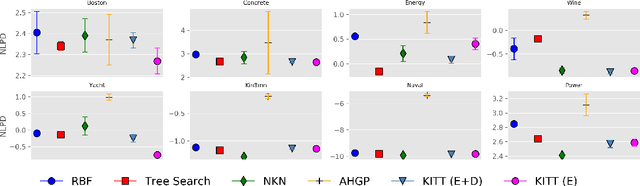
Kernel selection plays a central role in determining the performance of Gaussian Process (GP) models, as the chosen kernel determines both the inductive biases and prior support of functions under the GP prior. This work addresses the challenge of constructing custom kernel functions for high-dimensional GP regression models. Drawing inspiration from recent progress in deep learning, we introduce a novel approach named KITT: Kernel Identification Through Transformers. KITT exploits a transformer-based architecture to generate kernel recommendations in under 0.1 seconds, which is several orders of magnitude faster than conventional kernel search algorithms. We train our model using synthetic data generated from priors over a vocabulary of known kernels. By exploiting the nature of the self-attention mechanism, KITT is able to process datasets with inputs of arbitrary dimension. We demonstrate that kernels chosen by KITT yield strong performance over a diverse collection of regression benchmarks.

The Minecraft Kernel: Modelling correlated Gaussian Processes in the Fourier domain

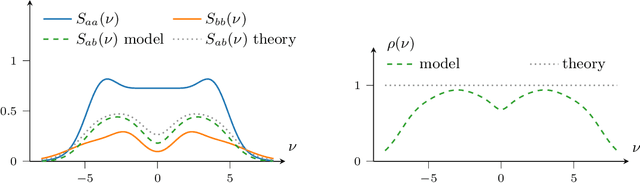
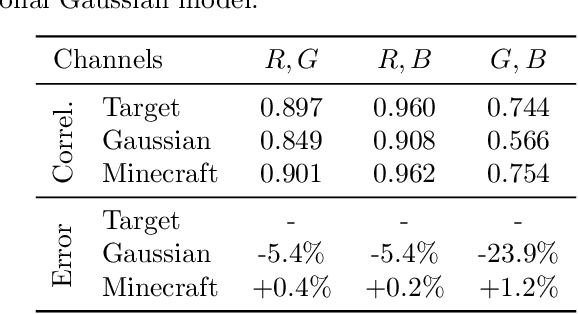
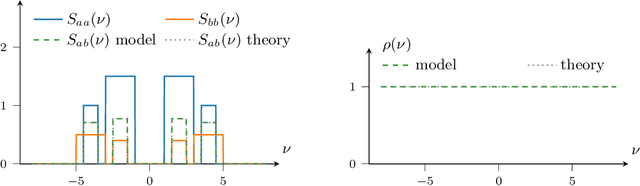
In the univariate setting, using the kernel spectral representation is an appealing approach for generating stationary covariance functions. However, performing the same task for multiple-output Gaussian processes is substantially more challenging. We demonstrate that current approaches to modelling cross-covariances with a spectral mixture kernel possess a critical blind spot. For a given pair of processes, the cross-covariance is not reproducible across the full range of permitted correlations, aside from the special case where their spectral densities are of identical shape. We present a solution to this issue by replacing the conventional Gaussian components of a spectral mixture with block components of finite bandwidth (i.e. rectangular step functions). The proposed family of kernel represents the first multi-output generalisation of the spectral mixture kernel that can approximate any stationary multi-output kernel to arbitrary precision.

Marginalised Gaussian Processes with Nested Sampling

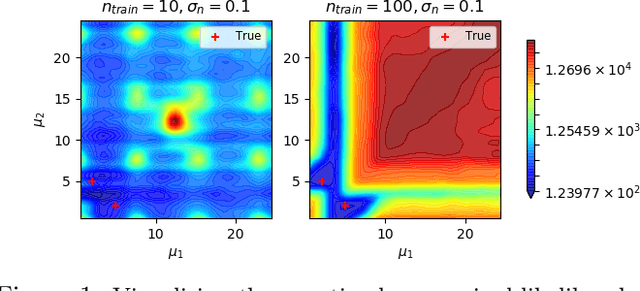
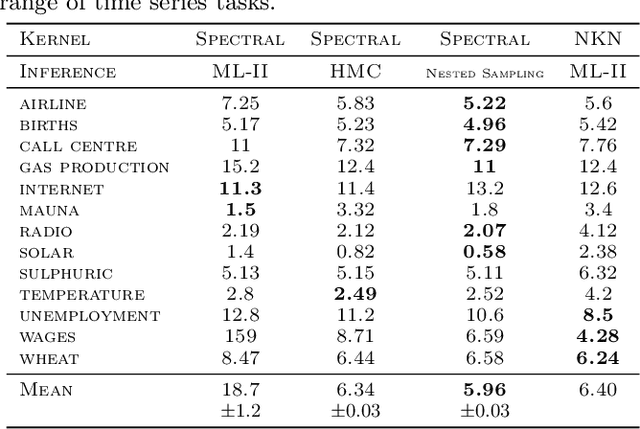
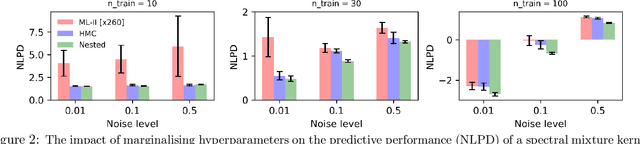
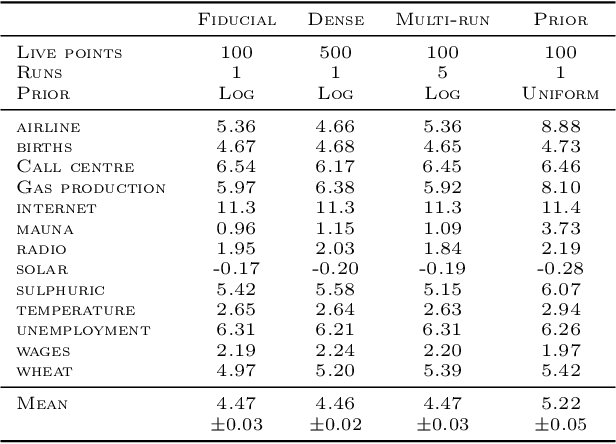
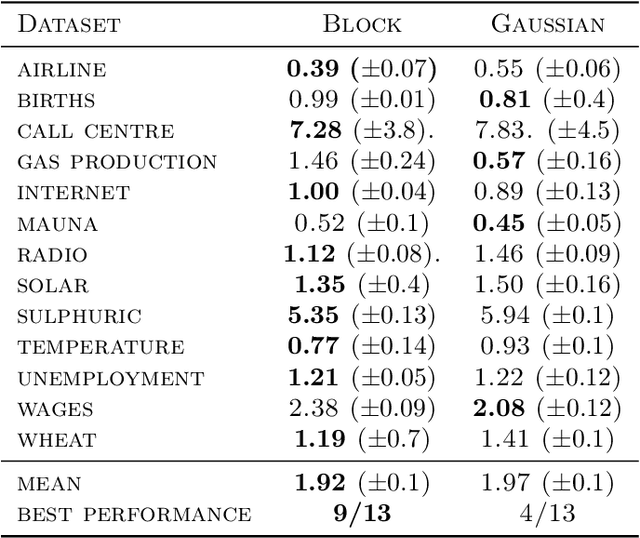
Gaussian Process (GPs) models are a rich distribution over functions with inductive biases controlled by a kernel function. Learning occurs through the optimisation of kernel hyperparameters using the marginal likelihood as the objective. This classical approach known as Type-II maximum likelihood (ML-II) yields point estimates of the hyperparameters, and continues to be the default method for training GPs. However, this approach risks underestimating predictive uncertainty and is prone to overfitting especially when there are many hyperparameters. Furthermore, gradient based optimisation makes ML-II point estimates highly susceptible to the presence of local minima. This work presents an alternative learning procedure where the hyperparameters of the kernel function are marginalised using Nested Sampling (NS), a technique that is well suited to sample from complex, multi-modal distributions. We focus on regression tasks with the spectral mixture (SM) class of kernels and find that a principled approach to quantifying model uncertainty leads to substantial gains in predictive performance across a range of synthetic and benchmark data sets. In this context, nested sampling is also found to offer a speed advantage over Hamiltonian Monte Carlo (HMC), widely considered to be the gold-standard in MCMC based inference.