Elvijs Sarkans
The Minecraft Kernel: Modelling correlated Gaussian Processes in the Fourier domain
Mar 11, 2021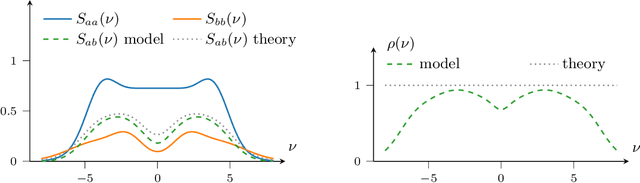
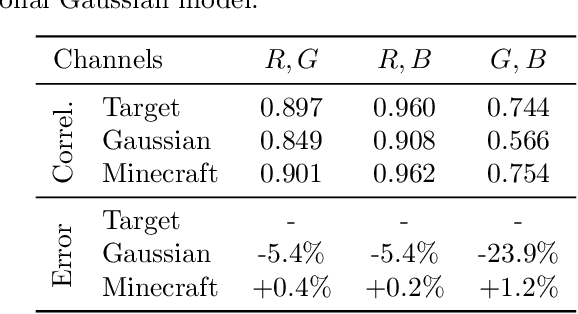
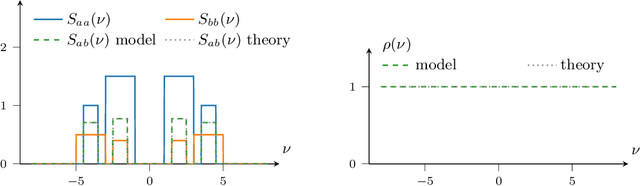
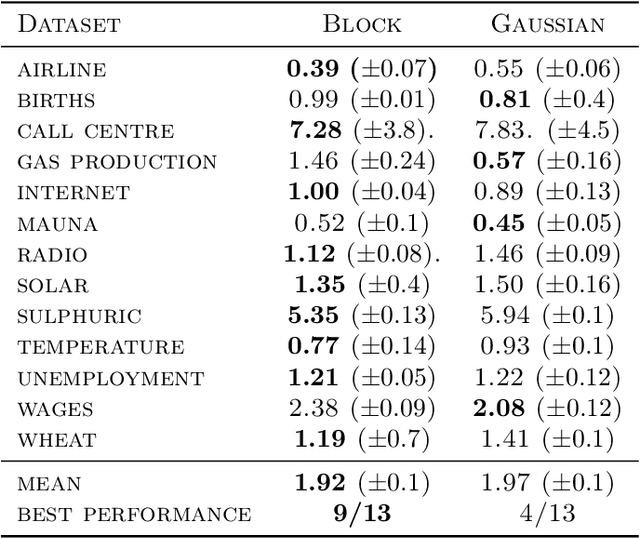
Abstract:In the univariate setting, using the kernel spectral representation is an appealing approach for generating stationary covariance functions. However, performing the same task for multiple-output Gaussian processes is substantially more challenging. We demonstrate that current approaches to modelling cross-covariances with a spectral mixture kernel possess a critical blind spot. For a given pair of processes, the cross-covariance is not reproducible across the full range of permitted correlations, aside from the special case where their spectral densities are of identical shape. We present a solution to this issue by replacing the conventional Gaussian components of a spectral mixture with block components of finite bandwidth (i.e. rectangular step functions). The proposed family of kernel represents the first multi-output generalisation of the spectral mixture kernel that can approximate any stationary multi-output kernel to arbitrary precision.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge