Kernel Identification Through Transformers

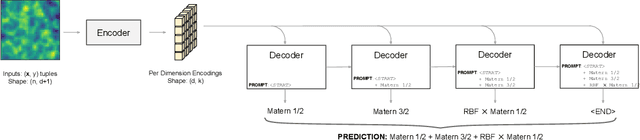
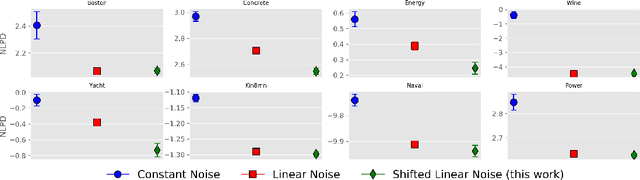
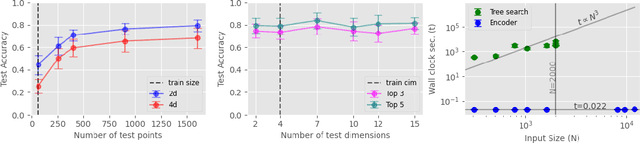
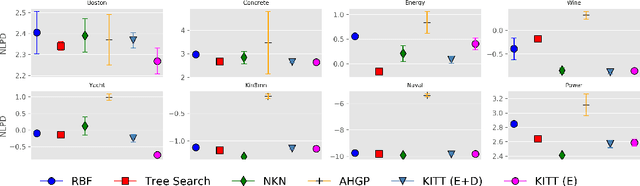
Kernel selection plays a central role in determining the performance of Gaussian Process (GP) models, as the chosen kernel determines both the inductive biases and prior support of functions under the GP prior. This work addresses the challenge of constructing custom kernel functions for high-dimensional GP regression models. Drawing inspiration from recent progress in deep learning, we introduce a novel approach named KITT: Kernel Identification Through Transformers. KITT exploits a transformer-based architecture to generate kernel recommendations in under 0.1 seconds, which is several orders of magnitude faster than conventional kernel search algorithms. We train our model using synthetic data generated from priors over a vocabulary of known kernels. By exploiting the nature of the self-attention mechanism, KITT is able to process datasets with inputs of arbitrary dimension. We demonstrate that kernels chosen by KITT yield strong performance over a diverse collection of regression benchmarks.

Deep Neural Networks as Point Estimates for Deep Gaussian Processes

Deep Gaussian processes (DGPs) have struggled for relevance in applications due to the challenges and cost associated with Bayesian inference. In this paper we propose a sparse variational approximation for DGPs for which the approximate posterior mean has the same mathematical structure as a Deep Neural Network (DNN). We make the forward pass through a DGP equivalent to a ReLU DNN by finding an interdomain transformation that represents the GP posterior mean as a sum of ReLU basis functions. This unification enables the initialisation and training of the DGP as a neural network, leveraging the well established practice in the deep learning community, and so greatly aiding the inference task. The experiments demonstrate improved accuracy and faster training compared to current DGP methods, while retaining favourable predictive uncertainties.

The Minecraft Kernel: Modelling correlated Gaussian Processes in the Fourier domain

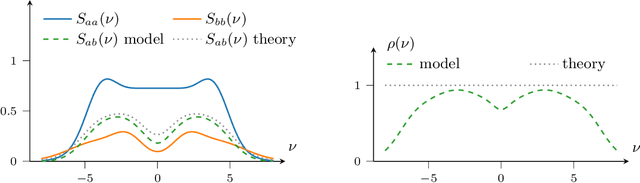
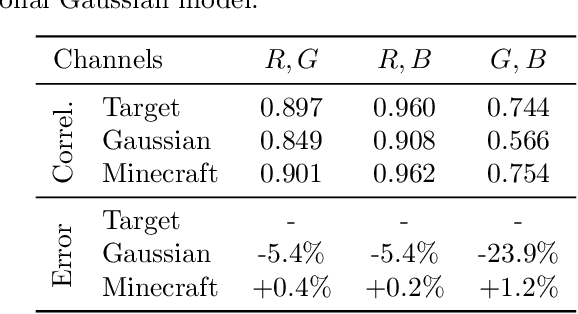
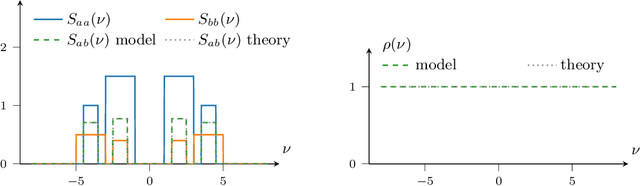
In the univariate setting, using the kernel spectral representation is an appealing approach for generating stationary covariance functions. However, performing the same task for multiple-output Gaussian processes is substantially more challenging. We demonstrate that current approaches to modelling cross-covariances with a spectral mixture kernel possess a critical blind spot. For a given pair of processes, the cross-covariance is not reproducible across the full range of permitted correlations, aside from the special case where their spectral densities are of identical shape. We present a solution to this issue by replacing the conventional Gaussian components of a spectral mixture with block components of finite bandwidth (i.e. rectangular step functions). The proposed family of kernel represents the first multi-output generalisation of the spectral mixture kernel that can approximate any stationary multi-output kernel to arbitrary precision.

A Tutorial on Sparse Gaussian Processes and Variational Inference

Gaussian processes (GPs) provide a framework for Bayesian inference that can offer principled uncertainty estimates for a large range of problems. For example, if we consider regression problems with Gaussian likelihoods, a GP model enjoys a posterior in closed form. However, identifying the posterior GP scales cubically with the number of training examples and requires to store all examples in memory. In order to overcome these obstacles, sparse GPs have been proposed that approximate the true posterior GP with pseudo-training examples. Importantly, the number of pseudo-training examples is user-defined and enables control over computational and memory complexity. In the general case, sparse GPs do not enjoy closed-form solutions and one has to resort to approximate inference. In this context, a convenient choice for approximate inference is variational inference (VI), where the problem of Bayesian inference is cast as an optimization problem -- namely, to maximize a lower bound of the log marginal likelihood. This paves the way for a powerful and versatile framework, where pseudo-training examples are treated as optimization arguments of the approximate posterior that are jointly identified together with hyperparameters of the generative model (i.e. prior and likelihood). The framework can naturally handle a wide scope of supervised learning problems, ranging from regression with heteroscedastic and non-Gaussian likelihoods to classification problems with discrete labels, but also multilabel problems. The purpose of this tutorial is to provide access to the basic matter for readers without prior knowledge in both GPs and VI. A proper exposition to the subject enables also access to more recent advances (like importance-weighted VI as well as inderdomain, multioutput and deep GPs) that can serve as an inspiration for new research ideas.

Matern Gaussian Processes on Graphs

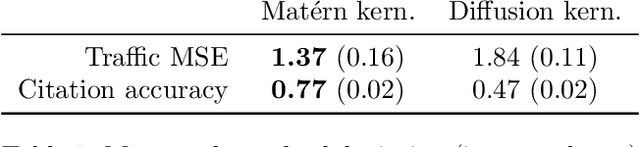
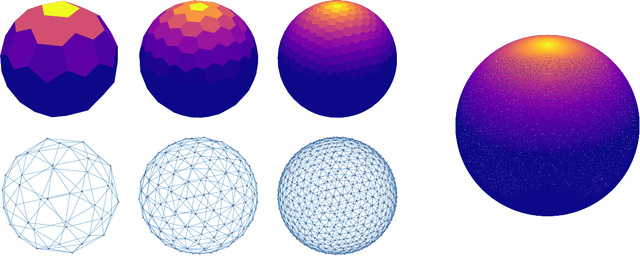
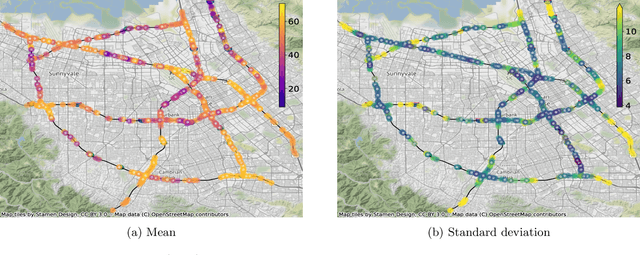
Gaussian processes are a versatile framework for learning unknown functions in a manner that permits one to utilize prior information about their properties. Although many different Gaussian process models are readily available when the input space is Euclidean, the choice is much more limited for Gaussian processes whose input space is an undirected graph. In this work, we leverage the stochastic partial differential equation characterization of Mat\'{e}rn Gaussian processes - a widely-used model class in the Euclidean setting - to study their analog for undirected graphs. We show that the resulting Gaussian processes inherit various attractive properties of their Euclidean and Riemannian analogs and provide techniques that allow them to be trained using standard methods, such as inducing points. This enables graph Mat\'{e}rn Gaussian processes to be employed in mini-batch and non-conjugate settings, thereby making them more accessible to practitioners and easier to deploy within larger learning frameworks.

Sparse Gaussian Processes with Spherical Harmonic Features

We introduce a new class of inter-domain variational Gaussian processes (GP) where data is mapped onto the unit hypersphere in order to use spherical harmonic representations. Our inference scheme is comparable to variational Fourier features, but it does not suffer from the curse of dimensionality, and leads to diagonal covariance matrices between inducing variables. This enables a speed-up in inference, because it bypasses the need to invert large covariance matrices. Our experiments show that our model is able to fit a regression model for a dataset with 6 million entries two orders of magnitude faster compared to standard sparse GPs, while retaining state of the art accuracy. We also demonstrate competitive performance on classification with non-conjugate likelihoods.

Automatic Tuning of Stochastic Gradient Descent with Bayesian Optimisation

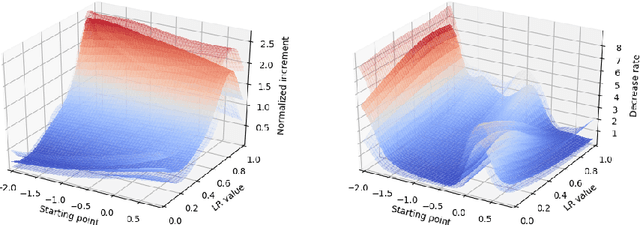
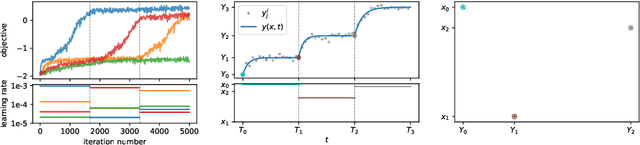
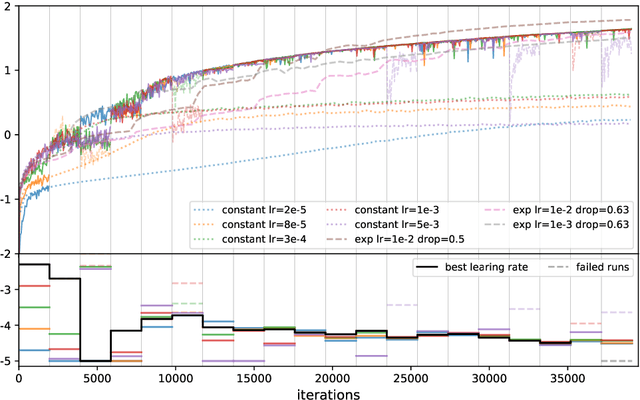
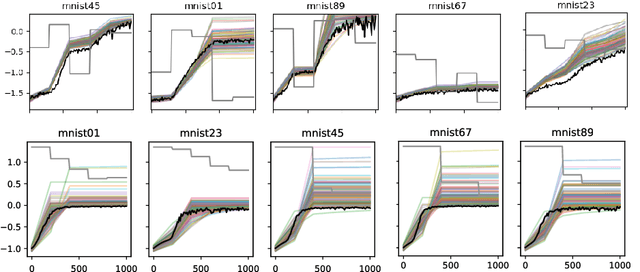
Many machine learning models require a training procedure based on running stochastic gradient descent. A key element for the efficiency of those algorithms is the choice of the learning rate schedule. While finding good learning rates schedules using Bayesian optimisation has been tackled by several authors, adapting it dynamically in a data-driven way is an open question. This is of high practical importance to users that need to train a single, expensive model. To tackle this problem, we introduce an original probabilistic model for traces of optimisers, based on latent Gaussian processes and an auto-/regressive formulation, that flexibly adjusts to abrupt changes of behaviours induced by new learning rate values. As illustrated, this model is well-suited to tackle a set of problems: first, for the on-line adaptation of the learning rate for a cold-started run; then, for tuning the schedule for a set of similar tasks (in a classical BO setup), as well as warm-starting it for a new task.

Regret Bounds for Noise-Free Bayesian Optimization

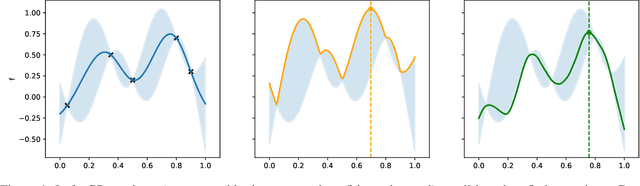
Bayesian optimisation is a powerful method for non-convex black-box optimization in low data regimes. However, the question of establishing tight upper bounds for common algorithms in the noiseless setting remains a largely open question. In this paper, we establish new and tightest bounds for two algorithms, namely GP-UCB and Thompson sampling, under the assumption that the objective function is smooth in terms of having a bounded norm in a Mat\'ern RKHS. Importantly, unlike several related works, we do not consider perfect knowledge of the kernel of the Gaussian process emulator used within the Bayesian optimization loop. This allows us to provide results for practical algorithms that sequentially estimate the Gaussian process kernel parameters from the available data.

Doubly Sparse Variational Gaussian Processes

The use of Gaussian process models is typically limited to datasets with a few tens of thousands of observations due to their complexity and memory footprint. The two most commonly used methods to overcome this limitation are 1) the variational sparse approximation which relies on inducing points and 2) the state-space equivalent formulation of Gaussian processes which can be seen as exploiting some sparsity in the precision matrix. We propose to take the best of both worlds: we show that the inducing point framework is still valid for state space models and that it can bring further computational and memory savings. Furthermore, we provide the natural gradient formulation for the proposed variational parameterisation. Finally, this work makes it possible to use the state-space formulation inside deep Gaussian process models as illustrated in one of the experiments.

Bayesian Quantile and Expectile Optimisation

Bayesian optimisation is widely used to optimise stochastic black box functions. While most strategies are focused on optimising conditional expectations, a large variety of applications require risk-averse decisions and alternative criteria accounting for the distribution tails need to be considered. In this paper, we propose new variational models for Bayesian quantile and expectile regression that are well-suited for heteroscedastic settings. Our models consist of two latent Gaussian processes accounting respectively for the conditional quantile (or expectile) and variance that are chained through asymmetric likelihood functions. Furthermore, we propose two Bayesian optimisation strategies, either derived from a GP-UCB or Thompson sampling, that are tailored to such models and that can accommodate large batches of points. As illustrated in the experimental section, the proposed approach clearly outperforms the state of the art.