The GeometricKernels Package: Heat and Matérn Kernels for Geometric Learning on Manifolds, Meshes, and Graphs

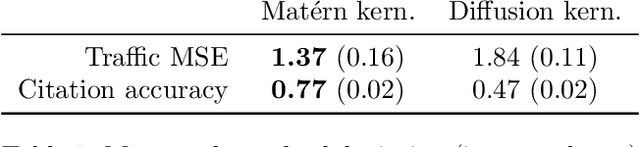
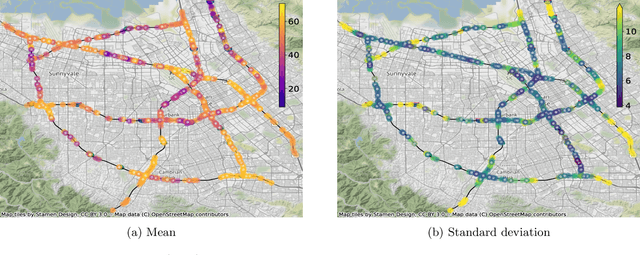
Kernels are a fundamental technical primitive in machine learning. In recent years, kernel-based methods such as Gaussian processes are becoming increasingly important in applications where quantifying uncertainty is of key interest. In settings that involve structured data defined on graphs, meshes, manifolds, or other related spaces, defining kernels with good uncertainty-quantification behavior, and computing their value numerically, is less straightforward than in the Euclidean setting. To address this difficulty, we present GeometricKernels, a software package which implements the geometric analogs of classical Euclidean squared exponential - also known as heat - and Mat\'ern kernels, which are widely-used in settings where uncertainty is of key interest. As a byproduct, we obtain the ability to compute Fourier-feature-type expansions, which are widely used in their own right, on a wide set of geometric spaces. Our implementation supports automatic differentiation in every major current framework simultaneously via a backend-agnostic design. In this companion paper to the package and its documentation, we outline the capabilities of the package and present an illustrated example of its interface. We also include a brief overview of the theory the package is built upon and provide some historic context in the appendix.

Pathwise Conditioning of Gaussian Processes

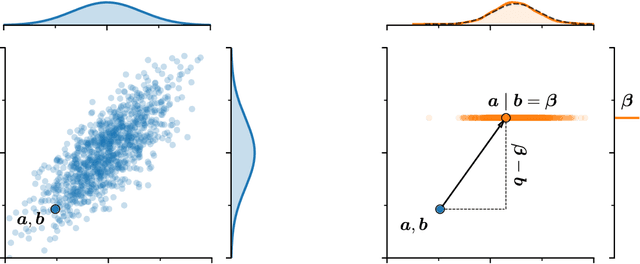
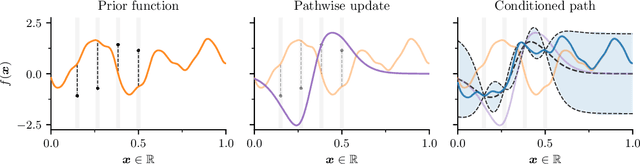
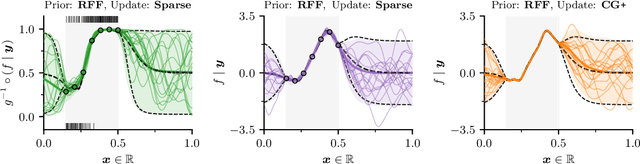
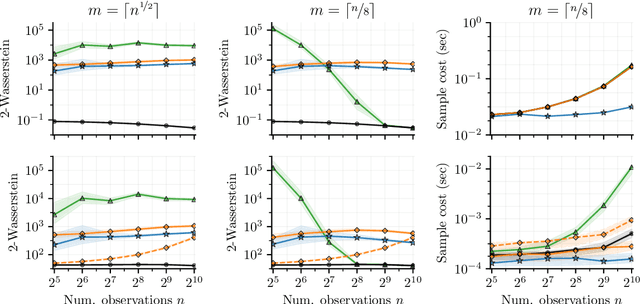
As Gaussian processes are integrated into increasingly complex problem settings, analytic solutions to quantities of interest become scarcer and scarcer. Monte Carlo methods act as a convenient bridge for connecting intractable mathematical expressions with actionable estimates via sampling. Conventional approaches for simulating Gaussian process posteriors view samples as vectors drawn from marginal distributions over process values at a finite number of input location. This distribution-based characterization leads to generative strategies that scale cubically in the size of the desired random vector. These methods are, therefore, prohibitively expensive in cases where high-dimensional vectors - let alone continuous functions - are required. In this work, we investigate a different line of reasoning. Rather than focusing on distributions, we articulate Gaussian conditionals at the level of random variables. We show how this pathwise interpretation of conditioning gives rise to a general family of approximations that lend themselves to fast sampling from Gaussian process posteriors. We analyze these methods, along with the approximation errors they introduce, from first principles. We then complement this theory, by exploring the practical ramifications of pathwise conditioning in a various applied settings.

Matern Gaussian Processes on Graphs

Gaussian processes are a versatile framework for learning unknown functions in a manner that permits one to utilize prior information about their properties. Although many different Gaussian process models are readily available when the input space is Euclidean, the choice is much more limited for Gaussian processes whose input space is an undirected graph. In this work, we leverage the stochastic partial differential equation characterization of Mat\'{e}rn Gaussian processes - a widely-used model class in the Euclidean setting - to study their analog for undirected graphs. We show that the resulting Gaussian processes inherit various attractive properties of their Euclidean and Riemannian analogs and provide techniques that allow them to be trained using standard methods, such as inducing points. This enables graph Mat\'{e}rn Gaussian processes to be employed in mini-batch and non-conjugate settings, thereby making them more accessible to practitioners and easier to deploy within larger learning frameworks.

Matern Gaussian processes on Riemannian manifolds

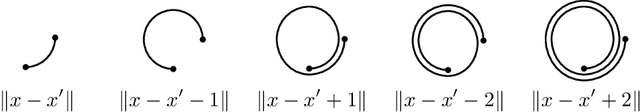
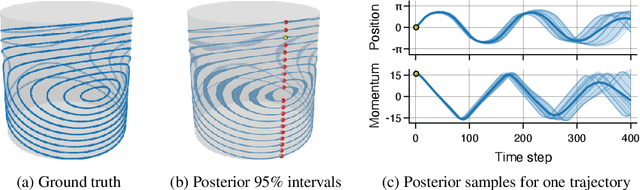
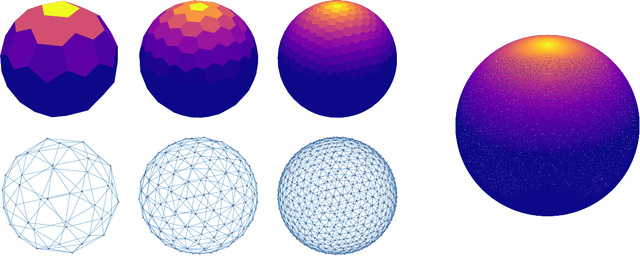
Gaussian processes are an effective model class for learning unknown functions, particularly in settings where accurately representing predictive uncertainty is of key importance. Motivated by applications in the physical sciences, the widely-used Mat\'{e}rn class of Gaussian processes has recently been generalized to model functions whose domains are Riemannian manifolds, by re-expressing said processes as solutions of stochastic partial differential equations. In this work, we propose techniques for computing the kernels of these processes via spectral theory of the Laplace--Beltrami operator in a fully constructive manner, thereby allowing them to be trained via standard scalable techniques such as inducing point methods. We also extend the generalization from the Mat\'{e}rn to the widely-used squared exponential Gaussian process. By allowing Riemannian Mat\'{e}rn Gaussian processes to be trained using well-understood techniques, our work enables their use in mini-batch, online, and non-conjugate settings, and makes them more accessible to machine learning practitioners.

Efficiently sampling functions from Gaussian process posteriors

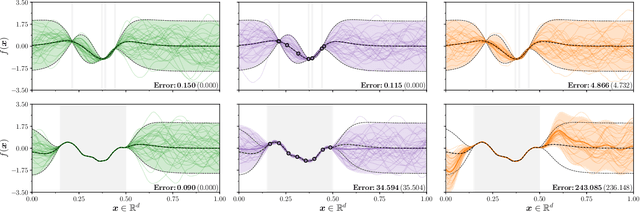
Gaussian processes are the gold standard for many real-world modeling problems, especially in cases where a model's success hinges upon its ability to faithfully represent predictive uncertainty. These problems typically exist as parts of larger frameworks, where quantities of interest are ultimately defined by integrating over posterior distributions. However, these algorithms' inner workings rarely allow for closed-form integration, giving rise to a need for Monte Carlo methods. Despite substantial progress in scaling up Gaussian processes to large training sets, methods for accurately generating draws from their posterior distributions still scale cubically in the number of test locations. We identify a decomposition of Gaussian processes that naturally lends itself to scalable sampling by enabling us to efficiently generate functions that accurately represent their posteriors. Building off of this factorization, we propose decoupled sampling, an easy-to-use and general-purpose approach for fast posterior sampling. Decoupled sampling works as a drop-in strategy that seamlessly pairs with sparse approximations to Gaussian processes to afford scalability both during training and at test time. In a series of experiments designed to test competing sampling schemes' statistical behaviors and practical ramifications, we empirically show that functions drawn using decoupled sampling faithfully represent Gaussian process posteriors at a fraction of the usual cost.