Fast and Robust Visuomotor Riemannian Flow Matching Policy

Diffusion-based visuomotor policies excel at learning complex robotic tasks by effectively combining visual data with high-dimensional, multi-modal action distributions. However, diffusion models often suffer from slow inference due to costly denoising processes or require complex sequential training arising from recent distilling approaches. This paper introduces Riemannian Flow Matching Policy (RFMP), a model that inherits the easy training and fast inference capabilities of flow matching (FM). Moreover, RFMP inherently incorporates geometric constraints commonly found in realistic robotic applications, as the robot state resides on a Riemannian manifold. To enhance the robustness of RFMP, we propose Stable RFMP (SRFMP), which leverages LaSalle's invariance principle to equip the dynamics of FM with stability to the support of a target Riemannian distribution. Rigorous evaluation on eight simulated and real-world tasks show that RFMP successfully learns and synthesizes complex sensorimotor policies on Euclidean and Riemannian spaces with efficient training and inference phases, outperforming Diffusion Policies while remaining competitive with Consistency Policies.

On Probabilistic Pullback Metrics on Latent Hyperbolic Manifolds

Gaussian Process Latent Variable Models (GPLVMs) have proven effective in capturing complex, high-dimensional data through lower-dimensional representations. Recent advances show that using Riemannian manifolds as latent spaces provides more flexibility to learn higher quality embeddings. This paper focuses on the hyperbolic manifold, a particularly suitable choice for modeling hierarchical relationships. While previous approaches relied on hyperbolic geodesics for interpolating the latent space, this often results in paths crossing low-data regions, leading to highly uncertain predictions. Instead, we propose augmenting the hyperbolic metric with a pullback metric to account for distortions introduced by the GPLVM's nonlinear mapping. Through various experiments, we demonstrate that geodesics on the pullback metric not only respect the geometry of the hyperbolic latent space but also align with the underlying data distribution, significantly reducing uncertainty in predictions.

A Riemannian Framework for Learning Reduced-order Lagrangian Dynamics

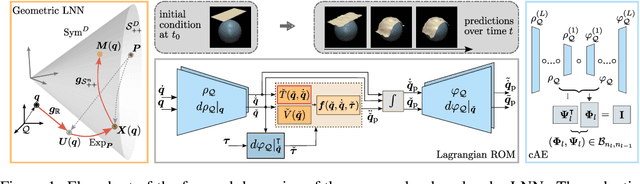
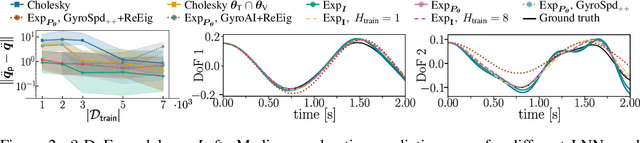
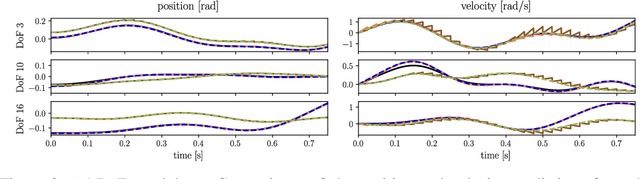
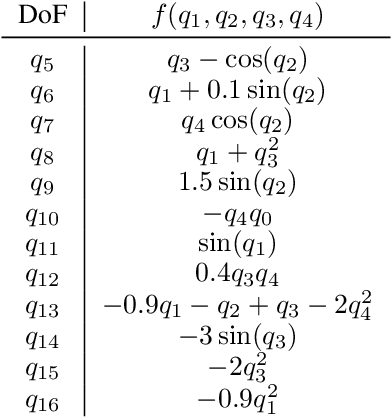
By incorporating physical consistency as inductive bias, deep neural networks display increased generalization capabilities and data efficiency in learning nonlinear dynamic models. However, the complexity of these models generally increases with the system dimensionality, requiring larger datasets, more complex deep networks, and significant computational effort. We propose a novel geometric network architecture to learn physically-consistent reduced-order dynamic parameters that accurately describe the original high-dimensional system behavior. This is achieved by building on recent advances in model-order reduction and by adopting a Riemannian perspective to jointly learn a structure-preserving latent space and the associated low-dimensional dynamics. Our approach enables accurate long-term predictions of the high-dimensional dynamics of rigid and deformable systems with increased data efficiency by inferring interpretable and physically plausible reduced Lagrangian models.

The GeometricKernels Package: Heat and Matérn Kernels for Geometric Learning on Manifolds, Meshes, and Graphs

Kernels are a fundamental technical primitive in machine learning. In recent years, kernel-based methods such as Gaussian processes are becoming increasingly important in applications where quantifying uncertainty is of key interest. In settings that involve structured data defined on graphs, meshes, manifolds, or other related spaces, defining kernels with good uncertainty-quantification behavior, and computing their value numerically, is less straightforward than in the Euclidean setting. To address this difficulty, we present GeometricKernels, a software package which implements the geometric analogs of classical Euclidean squared exponential - also known as heat - and Mat\'ern kernels, which are widely-used in settings where uncertainty is of key interest. As a byproduct, we obtain the ability to compute Fourier-feature-type expansions, which are widely used in their own right, on a wide set of geometric spaces. Our implementation supports automatic differentiation in every major current framework simultaneously via a backend-agnostic design. In this companion paper to the package and its documentation, we outline the capabilities of the package and present an illustrated example of its interface. We also include a brief overview of the theory the package is built upon and provide some historic context in the appendix.

Riemannian Flow Matching Policy for Robot Motion Learning

We introduce Riemannian Flow Matching Policies (RFMP), a novel model for learning and synthesizing robot visuomotor policies. RFMP leverages the efficient training and inference capabilities of flow matching methods. By design, RFMP inherits the strengths of flow matching: the ability to encode high-dimensional multimodal distributions, commonly encountered in robotic tasks, and a very simple and fast inference process. We demonstrate the applicability of RFMP to both state-based and vision-conditioned robot motion policies. Notably, as the robot state resides on a Riemannian manifold, RFMP inherently incorporates geometric awareness, which is crucial for realistic robotic tasks. To evaluate RFMP, we conduct two proof-of-concept experiments, comparing its performance against Diffusion Policies. Although both approaches successfully learn the considered tasks, our results show that RFMP provides smoother action trajectories with significantly lower inference times.

Bi-KVIL: Keypoints-based Visual Imitation Learning of Bimanual Manipulation Tasks

Visual imitation learning has achieved impressive progress in learning unimanual manipulation tasks from a small set of visual observations, thanks to the latest advances in computer vision. However, learning bimanual coordination strategies and complex object relations from bimanual visual demonstrations, as well as generalizing them to categorical objects in novel cluttered scenes remain unsolved challenges. In this paper, we extend our previous work on keypoints-based visual imitation learning (\mbox{K-VIL})~\cite{gao_kvil_2023} to bimanual manipulation tasks. The proposed Bi-KVIL jointly extracts so-called \emph{Hybrid Master-Slave Relationships} (HMSR) among objects and hands, bimanual coordination strategies, and sub-symbolic task representations. Our bimanual task representation is object-centric, embodiment-independent, and viewpoint-invariant, thus generalizing well to categorical objects in novel scenes. We evaluate our approach in various real-world applications, showcasing its ability to learn fine-grained bimanual manipulation tasks from a small number of human demonstration videos. Videos and source code are available at https://sites.google.com/view/bi-kvil.

Incremental Learning of Full-Pose Via-Point Movement Primitives on Riemannian Manifolds

Movement primitives (MPs) are compact representations of robot skills that can be learned from demonstrations and combined into complex behaviors. However, merely equipping robots with a fixed set of innate MPs is insufficient to deploy them in dynamic and unpredictable environments. Instead, the full potential of MPs remains to be attained via adaptable, large-scale MP libraries. In this paper, we propose a set of seven fundamental operations to incrementally learn, improve, and re-organize MP libraries. To showcase their applicability, we provide explicit formulations of the spatial operations for libraries composed of Via-Point Movement Primitives (VMPs). By building on Riemannian manifold theory, our approach enables the incremental learning of all parameters of position and orientation VMPs within a library. Moreover, our approach stores a fixed number of parameters, thus complying with the essential principles of incremental learning. We evaluate our approach to incrementally learn a VMP library from motion capture data provided sequentially.

Transfer Learning in Robotics: An Upcoming Breakthrough? A Review of Promises and Challenges

Transfer learning is a conceptually-enticing paradigm in pursuit of truly intelligent embodied agents. The core concept -- reusing prior knowledge to learn in and from novel situations -- is successfully leveraged by humans to handle novel situations. In recent years, transfer learning has received renewed interest from the community from different perspectives, including imitation learning, domain adaptation, and transfer of experience from simulation to the real world, among others. In this paper, we unify the concept of transfer learning in robotics and provide the first taxonomy of its kind considering the key concepts of robot, task, and environment. Through a review of the promises and challenges in the field, we identify the need of transferring at different abstraction levels, the need of quantifying the transfer gap and the quality of transfer, as well as the dangers of negative transfer. Via this position paper, we hope to channel the effort of the community towards the most significant roadblocks to realize the full potential of transfer learning in robotics.

Unraveling the Single Tangent Space Fallacy: An Analysis and Clarification for Applying Riemannian Geometry in Robot Learning

In the realm of robotics, numerous downstream robotics tasks leverage machine learning methods for processing, modeling, or synthesizing data. Often, this data comprises variables that inherently carry geometric constraints, such as the unit-norm condition of quaternions representing rigid-body orientations or the positive definiteness of stiffness and manipulability ellipsoids. Handling such geometric constraints effectively requires the incorporation of tools from differential geometry into the formulation of machine learning methods. In this context, Riemannian manifolds emerge as a powerful mathematical framework to handle such geometric constraints. Nevertheless, their recent adoption in robot learning has been largely characterized by a mathematically-flawed simplification, hereinafter referred to as the ``single tangent space fallacy". This approach involves merely projecting the data of interest onto a single tangent (Euclidean) space, over which an off-the-shelf learning algorithm is applied. This paper provides a theoretical elucidation of various misconceptions surrounding this approach and offers experimental evidence of its shortcomings. Finally, it presents valuable insights to promote best practices when employing Riemannian geometry within robot learning applications.

On the Design of Region-Avoiding Metrics for Collision-Safe Motion Generation on Riemannian Manifolds

The generation of energy-efficient and dynamic-aware robot motions that satisfy constraints such as joint limits, self-collisions, and collisions with the environment remains a challenge. In this context, Riemannian geometry offers promising solutions by identifying robot motions with geodesics on the so-called configuration space manifold. While this manifold naturally considers the intrinsic robot dynamics, constraints such as joint limits, self-collisions, and collisions with the environment remain overlooked. In this paper, we propose a modification of the Riemannian metric of the configuration space manifold allowing for the generation of robot motions as geodesics that efficiently avoid given regions. We introduce a class of Riemannian metrics based on barrier functions that guarantee strict region avoidance by systematically generating accelerations away from no-go regions in joint and task space. We evaluate the proposed Riemannian metric to generate energy-efficient, dynamic-aware, and collision-free motions of a humanoid robot as geodesics and sequences thereof.