Pushing Everything Everywhere All At Once: Probabilistic Prehensile Pushing

We address prehensile pushing, the problem of manipulating a grasped object by pushing against the environment. Our solution is an efficient nonlinear trajectory optimization problem relaxed from an exact mixed integer non-linear trajectory optimization formulation. The critical insight is recasting the external pushers (environment) as a discrete probability distribution instead of binary variables and minimizing the entropy of the distribution. The probabilistic reformulation allows all pushers to be used simultaneously, but at the optimum, the probability mass concentrates onto one due to the entropy minimization. We numerically compare our method against a state-of-the-art sampling-based baseline on a prehensile pushing task. The results demonstrate that our method finds trajectories 8 times faster and at a 20 times lower cost than the baseline. Finally, we demonstrate that a simulated and real Franka Panda robot can successfully manipulate different objects following the trajectories proposed by our method. Supplementary materials are available at https://probabilistic-prehensile-pushing.github.io/.

A Riemannian Framework for Learning Reduced-order Lagrangian Dynamics

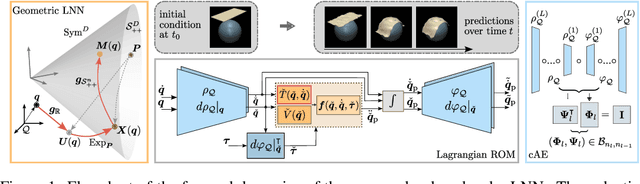
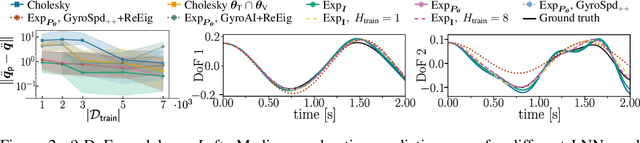
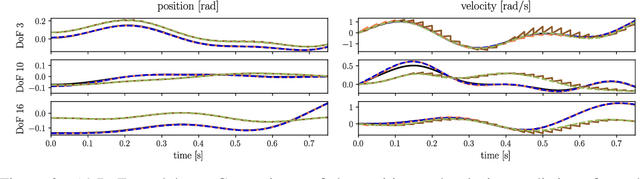
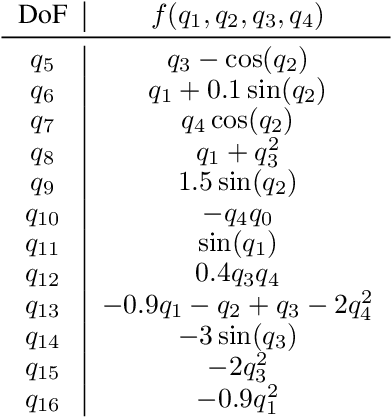
By incorporating physical consistency as inductive bias, deep neural networks display increased generalization capabilities and data efficiency in learning nonlinear dynamic models. However, the complexity of these models generally increases with the system dimensionality, requiring larger datasets, more complex deep networks, and significant computational effort. We propose a novel geometric network architecture to learn physically-consistent reduced-order dynamic parameters that accurately describe the original high-dimensional system behavior. This is achieved by building on recent advances in model-order reduction and by adopting a Riemannian perspective to jointly learn a structure-preserving latent space and the associated low-dimensional dynamics. Our approach enables accurate long-term predictions of the high-dimensional dynamics of rigid and deformable systems with increased data efficiency by inferring interpretable and physically plausible reduced Lagrangian models.