Leonel Rozo
Contact Wasserstein Geodesics for Non-Conservative Schrödinger Bridges
Nov 11, 2025Abstract:The Schrödinger Bridge provides a principled framework for modeling stochastic processes between distributions; however, existing methods are limited by energy-conservation assumptions, which constrains the bridge's shape preventing it from model varying-energy phenomena. To overcome this, we introduce the non-conservative generalized Schrödinger bridge (NCGSB), a novel, energy-varying reformulation based on contact Hamiltonian mechanics. By allowing energy to change over time, the NCGSB provides a broader class of real-world stochastic processes, capturing richer and more faithful intermediate dynamics. By parameterizing the Wasserstein manifold, we lift the bridge problem to a tractable geodesic computation in a finite-dimensional space. Unlike computationally expensive iterative solutions, our contact Wasserstein geodesic (CWG) is naturally implemented via a ResNet architecture and relies on a non-iterative solver with near-linear complexity. Furthermore, CWG supports guided generation by modulating a task-specific distance metric. We validate our framework on tasks including manifold navigation, molecular dynamics predictions, and image generation, demonstrating its practical benefits and versatility.
Towards Safe Imitation Learning via Potential Field-Guided Flow Matching
Aug 12, 2025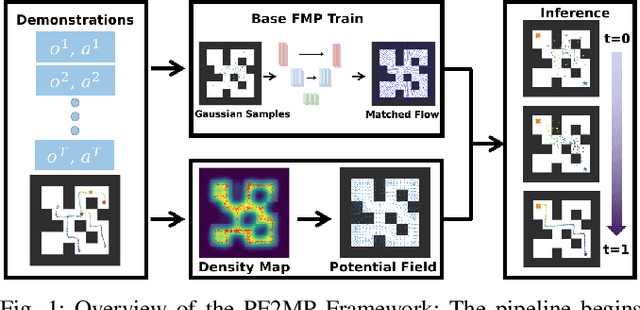
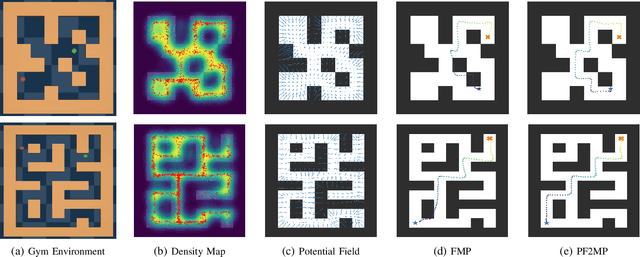
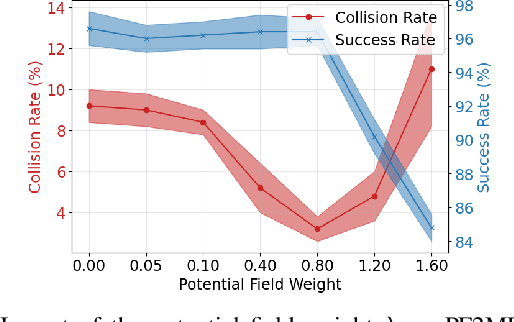

Abstract:Deep generative models, particularly diffusion and flow matching models, have recently shown remarkable potential in learning complex policies through imitation learning. However, the safety of generated motions remains overlooked, particularly in complex environments with inherent obstacles. In this work, we address this critical gap by proposing Potential Field-Guided Flow Matching Policy (PF2MP), a novel approach that simultaneously learns task policies and extracts obstacle-related information, represented as a potential field, from the same set of successful demonstrations. During inference, PF2MP modulates the flow matching vector field via the learned potential field, enabling safe motion generation. By leveraging these complementary fields, our approach achieves improved safety without compromising task success across diverse environments, such as navigation tasks and robotic manipulation scenarios. We evaluate PF2MP in both simulation and real-world settings, demonstrating its effectiveness in task space and joint space control. Experimental results demonstrate that PF2MP enhances safety, achieving a significant reduction of collisions compared to baseline policies. This work paves the way for safer motion generation in unstructured and obstaclerich environments.
Diffeomorphic Obstacle Avoidance for Contractive Dynamical Systems via Implicit Representations
Apr 26, 2025



Abstract:Ensuring safety and robustness of robot skills is becoming crucial as robots are required to perform increasingly complex and dynamic tasks. The former is essential when performing tasks in cluttered environments, while the latter is relevant to overcome unseen task situations. This paper addresses the challenge of ensuring both safety and robustness in dynamic robot skills learned from demonstrations. Specifically, we build on neural contractive dynamical systems to provide robust extrapolation of the learned skills, while designing a full-body obstacle avoidance strategy that preserves contraction stability via diffeomorphic transforms. This is particularly crucial in complex environments where implicit scene representations, such as Signed Distance Fields (SDFs), are necessary. To this end, our framework called Signed Distance Field Diffeomorphic Transform, leverages SDFs and flow-based diffeomorphisms to achieve contraction-preserving obstacle avoidance. We thoroughly evaluate our framework on synthetic datasets and several real-world robotic tasks in a kitchen environment. Our results show that our approach locally adapts the learned contractive vector field while staying close to the learned dynamics and without introducing highly-curved motion paths, thus outperforming several state-of-the-art methods.
Riemann$^2$: Learning Riemannian Submanifolds from Riemannian Data
Mar 07, 2025Abstract:Latent variable models are powerful tools for learning low-dimensional manifolds from high-dimensional data. However, when dealing with constrained data such as unit-norm vectors or symmetric positive-definite matrices, existing approaches ignore the underlying geometric constraints or fail to provide meaningful metrics in the latent space. To address these limitations, we propose to learn Riemannian latent representations of such geometric data. To do so, we estimate the pullback metric induced by a Wrapped Gaussian Process Latent Variable Model, which explicitly accounts for the data geometry. This enables us to define geometry-aware notions of distance and shortest paths in the latent space, while ensuring that our model only assigns probability mass to the data manifold. This generalizes previous work and allows us to handle complex tasks in various domains, including robot motion synthesis and analysis of brain connectomes.
Fast and Robust Visuomotor Riemannian Flow Matching Policy
Dec 14, 2024



Abstract:Diffusion-based visuomotor policies excel at learning complex robotic tasks by effectively combining visual data with high-dimensional, multi-modal action distributions. However, diffusion models often suffer from slow inference due to costly denoising processes or require complex sequential training arising from recent distilling approaches. This paper introduces Riemannian Flow Matching Policy (RFMP), a model that inherits the easy training and fast inference capabilities of flow matching (FM). Moreover, RFMP inherently incorporates geometric constraints commonly found in realistic robotic applications, as the robot state resides on a Riemannian manifold. To enhance the robustness of RFMP, we propose Stable RFMP (SRFMP), which leverages LaSalle's invariance principle to equip the dynamics of FM with stability to the support of a target Riemannian distribution. Rigorous evaluation on eight simulated and real-world tasks show that RFMP successfully learns and synthesizes complex sensorimotor policies on Euclidean and Riemannian spaces with efficient training and inference phases, outperforming Diffusion Policies while remaining competitive with Consistency Policies.
Extended Neural Contractive Dynamical Systems: On Multiple Tasks and Riemannian Safety Regions
Nov 20, 2024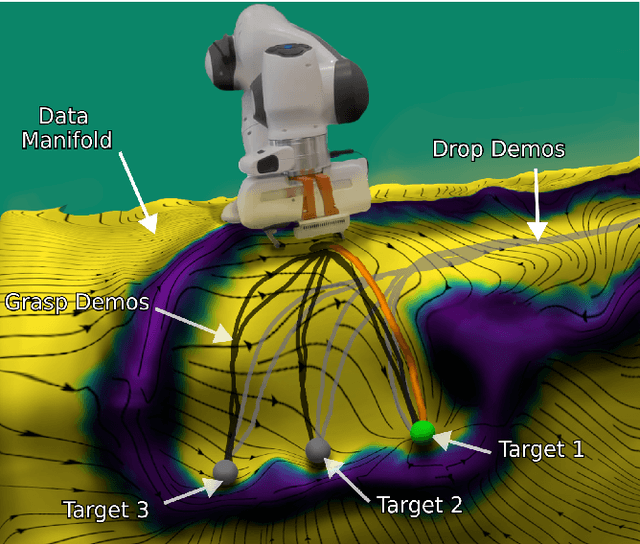

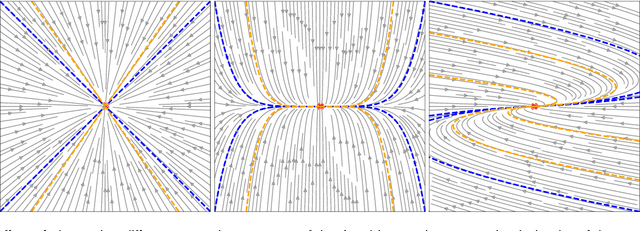
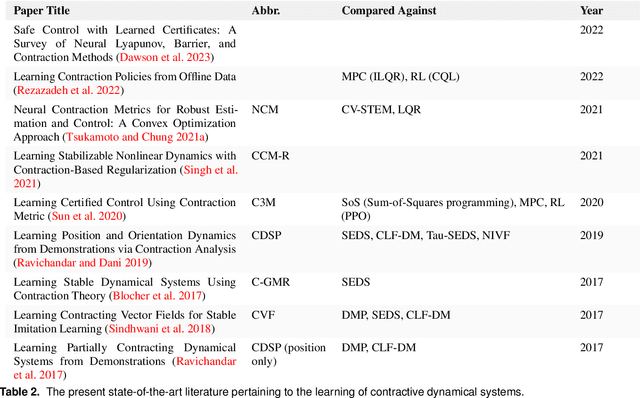
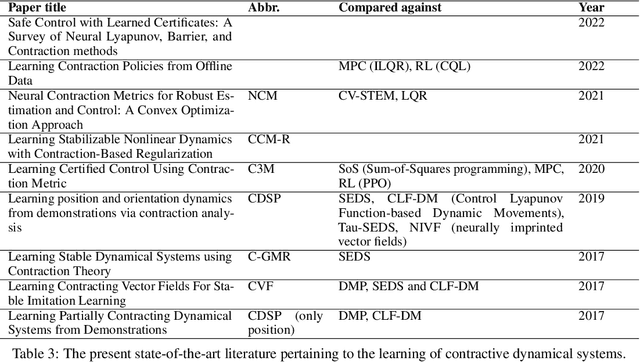
Abstract:Stability guarantees are crucial when ensuring that a fully autonomous robot does not take undesirable or potentially harmful actions. We recently proposed the Neural Contractive Dynamical Systems (NCDS), which is a neural network architecture that guarantees contractive stability. With this, learning-from-demonstrations approaches can trivially provide stability guarantees. However, our early work left several unanswered questions, which we here address. Beyond providing an in-depth explanation of NCDS, this paper extends the framework with more careful regularization, a conditional variant of the framework for handling multiple tasks, and an uncertainty-driven approach to latent obstacle avoidance. Experiments verify that the developed system has the flexibility of ordinary neural networks while providing the stability guarantees needed for autonomous robotics.
On Probabilistic Pullback Metrics on Latent Hyperbolic Manifolds
Oct 28, 2024Abstract:Gaussian Process Latent Variable Models (GPLVMs) have proven effective in capturing complex, high-dimensional data through lower-dimensional representations. Recent advances show that using Riemannian manifolds as latent spaces provides more flexibility to learn higher quality embeddings. This paper focuses on the hyperbolic manifold, a particularly suitable choice for modeling hierarchical relationships. While previous approaches relied on hyperbolic geodesics for interpolating the latent space, this often results in paths crossing low-data regions, leading to highly uncertain predictions. Instead, we propose augmenting the hyperbolic metric with a pullback metric to account for distortions introduced by the GPLVM's nonlinear mapping. Through various experiments, we demonstrate that geodesics on the pullback metric not only respect the geometry of the hyperbolic latent space but also align with the underlying data distribution, significantly reducing uncertainty in predictions.
The GeometricKernels Package: Heat and Matérn Kernels for Geometric Learning on Manifolds, Meshes, and Graphs
Jul 10, 2024
Abstract:Kernels are a fundamental technical primitive in machine learning. In recent years, kernel-based methods such as Gaussian processes are becoming increasingly important in applications where quantifying uncertainty is of key interest. In settings that involve structured data defined on graphs, meshes, manifolds, or other related spaces, defining kernels with good uncertainty-quantification behavior, and computing their value numerically, is less straightforward than in the Euclidean setting. To address this difficulty, we present GeometricKernels, a software package which implements the geometric analogs of classical Euclidean squared exponential - also known as heat - and Mat\'ern kernels, which are widely-used in settings where uncertainty is of key interest. As a byproduct, we obtain the ability to compute Fourier-feature-type expansions, which are widely used in their own right, on a wide set of geometric spaces. Our implementation supports automatic differentiation in every major current framework simultaneously via a backend-agnostic design. In this companion paper to the package and its documentation, we outline the capabilities of the package and present an illustrated example of its interface. We also include a brief overview of the theory the package is built upon and provide some historic context in the appendix.
Riemannian Flow Matching Policy for Robot Motion Learning
Mar 15, 2024Abstract:We introduce Riemannian Flow Matching Policies (RFMP), a novel model for learning and synthesizing robot visuomotor policies. RFMP leverages the efficient training and inference capabilities of flow matching methods. By design, RFMP inherits the strengths of flow matching: the ability to encode high-dimensional multimodal distributions, commonly encountered in robotic tasks, and a very simple and fast inference process. We demonstrate the applicability of RFMP to both state-based and vision-conditioned robot motion policies. Notably, as the robot state resides on a Riemannian manifold, RFMP inherently incorporates geometric awareness, which is crucial for realistic robotic tasks. To evaluate RFMP, we conduct two proof-of-concept experiments, comparing its performance against Diffusion Policies. Although both approaches successfully learn the considered tasks, our results show that RFMP provides smoother action trajectories with significantly lower inference times.
Neural Contractive Dynamical Systems
Jan 17, 2024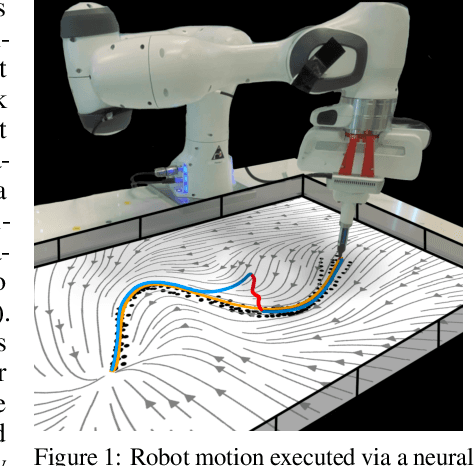


Abstract:Stability guarantees are crucial when ensuring a fully autonomous robot does not take undesirable or potentially harmful actions. Unfortunately, global stability guarantees are hard to provide in dynamical systems learned from data, especially when the learned dynamics are governed by neural networks. We propose a novel methodology to learn neural contractive dynamical systems, where our neural architecture ensures contraction, and hence, global stability. To efficiently scale the method to high-dimensional dynamical systems, we develop a variant of the variational autoencoder that learns dynamics in a low-dimensional latent representation space while retaining contractive stability after decoding. We further extend our approach to learning contractive systems on the Lie group of rotations to account for full-pose end-effector dynamic motions. The result is the first highly flexible learning architecture that provides contractive stability guarantees with capability to perform obstacle avoidance. Empirically, we demonstrate that our approach encodes the desired dynamics more accurately than the current state-of-the-art, which provides less strong stability guarantees.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge