The GeometricKernels Package: Heat and Matérn Kernels for Geometric Learning on Manifolds, Meshes, and Graphs

Kernels are a fundamental technical primitive in machine learning. In recent years, kernel-based methods such as Gaussian processes are becoming increasingly important in applications where quantifying uncertainty is of key interest. In settings that involve structured data defined on graphs, meshes, manifolds, or other related spaces, defining kernels with good uncertainty-quantification behavior, and computing their value numerically, is less straightforward than in the Euclidean setting. To address this difficulty, we present GeometricKernels, a software package which implements the geometric analogs of classical Euclidean squared exponential - also known as heat - and Mat\'ern kernels, which are widely-used in settings where uncertainty is of key interest. As a byproduct, we obtain the ability to compute Fourier-feature-type expansions, which are widely used in their own right, on a wide set of geometric spaces. Our implementation supports automatic differentiation in every major current framework simultaneously via a backend-agnostic design. In this companion paper to the package and its documentation, we outline the capabilities of the package and present an illustrated example of its interface. We also include a brief overview of the theory the package is built upon and provide some historic context in the appendix.

DEFT: Efficient Finetuning of Conditional Diffusion Models by Learning the Generalised $h$-transform

Generative modelling paradigms based on denoising diffusion processes have emerged as a leading candidate for conditional sampling in inverse problems. In many real-world applications, we often have access to large, expensively trained unconditional diffusion models, which we aim to exploit for improving conditional sampling. Most recent approaches are motivated heuristically and lack a unifying framework, obscuring connections between them. Further, they often suffer from issues such as being very sensitive to hyperparameters, being expensive to train or needing access to weights hidden behind a closed API. In this work, we unify conditional training and sampling using the mathematically well-understood Doob's h-transform. This new perspective allows us to unify many existing methods under a common umbrella. Under this framework, we propose DEFT (Doob's h-transform Efficient FineTuning), a new approach for conditional generation that simply fine-tunes a very small network to quickly learn the conditional $h$-transform, while keeping the larger unconditional network unchanged. DEFT is much faster than existing baselines while achieving state-of-the-art performance across a variety of linear and non-linear benchmarks. On image reconstruction tasks, we achieve speedups of up to 1.6$\times$, while having the best perceptual quality on natural images and reconstruction performance on medical images.

A framework for conditional diffusion modelling with applications in motif scaffolding for protein design

Many protein design applications, such as binder or enzyme design, require scaffolding a structural motif with high precision. Generative modelling paradigms based on denoising diffusion processes emerged as a leading candidate to address this motif scaffolding problem and have shown early experimental success in some cases. In the diffusion paradigm, motif scaffolding is treated as a conditional generation task, and several conditional generation protocols were proposed or imported from the Computer Vision literature. However, most of these protocols are motivated heuristically, e.g. via analogies to Langevin dynamics, and lack a unifying framework, obscuring connections between the different approaches. In this work, we unify conditional training and conditional sampling procedures under one common framework based on the mathematically well-understood Doob's h-transform. This new perspective allows us to draw connections between existing methods and propose a new variation on existing conditional training protocols. We illustrate the effectiveness of this new protocol in both, image outpainting and motif scaffolding and find that it outperforms standard methods.

Geometric Neural Diffusion Processes

Denoising diffusion models have proven to be a flexible and effective paradigm for generative modelling. Their recent extension to infinite dimensional Euclidean spaces has allowed for the modelling of stochastic processes. However, many problems in the natural sciences incorporate symmetries and involve data living in non-Euclidean spaces. In this work, we extend the framework of diffusion models to incorporate a series of geometric priors in infinite-dimension modelling. We do so by a) constructing a noising process which admits, as limiting distribution, a geometric Gaussian process that transforms under the symmetry group of interest, and b) approximating the score with a neural network that is equivariant w.r.t. this group. We show that with these conditions, the generative functional model admits the same symmetry. We demonstrate scalability and capacity of the model, using a novel Langevin-based conditional sampler, to fit complex scalar and vector fields, with Euclidean and spherical codomain, on synthetic and real-world weather data.

Spherical Inducing Features for Orthogonally-Decoupled Gaussian Processes

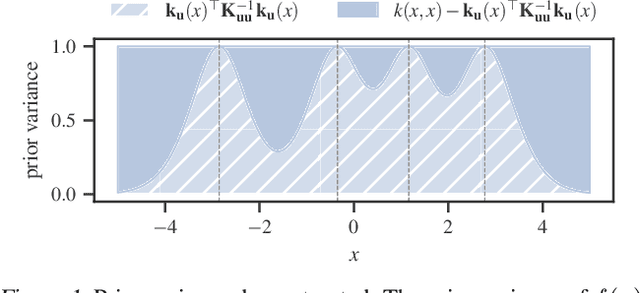
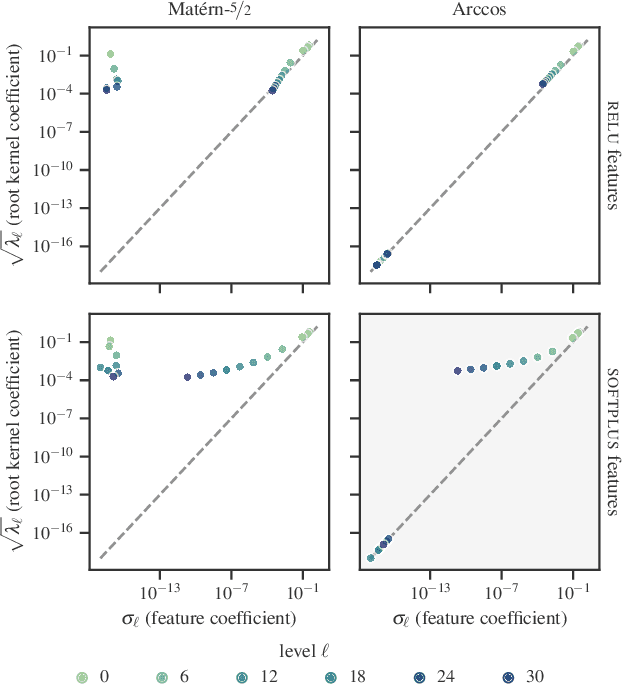
Despite their many desirable properties, Gaussian processes (GPs) are often compared unfavorably to deep neural networks (NNs) for lacking the ability to learn representations. Recent efforts to bridge the gap between GPs and deep NNs have yielded a new class of inter-domain variational GPs in which the inducing variables correspond to hidden units of a feedforward NN. In this work, we examine some practical issues associated with this approach and propose an extension that leverages the orthogonal decomposition of GPs to mitigate these limitations. In particular, we introduce spherical inter-domain features to construct more flexible data-dependent basis functions for both the principal and orthogonal components of the GP approximation and show that incorporating NN activation features under this framework not only alleviates these shortcomings but is more scalable than alternative strategies. Experiments on multiple benchmark datasets demonstrate the effectiveness of our approach.

Memory-Based Meta-Learning on Non-Stationary Distributions

Memory-based meta-learning is a technique for approximating Bayes-optimal predictors. Under fairly general conditions, minimizing sequential prediction error, measured by the log loss, leads to implicit meta-learning. The goal of this work is to investigate how far this interpretation can be realized by current sequence prediction models and training regimes. The focus is on piecewise stationary sources with unobserved switching-points, which arguably capture an important characteristic of natural language and action-observation sequences in partially observable environments. We show that various types of memory-based neural models, including Transformers, LSTMs, and RNNs can learn to accurately approximate known Bayes-optimal algorithms and behave as if performing Bayesian inference over the latent switching-points and the latent parameters governing the data distribution within each segment.

Neural Diffusion Processes

Gaussian processes provide an elegant framework for specifying prior and posterior distributions over functions. They are, however, also computationally expensive, and limited by the expressivity of their covariance function. We propose Neural Diffusion Processes (NDPs), a novel approach based upon diffusion models, that learn to sample from distributions over functions. Using a novel attention block, we can incorporate properties of stochastic processes, such as exchangeability, directly into the NDP's architecture. We empirically show that NDPs are able to capture functional distributions that are close to the true Bayesian posterior of a Gaussian process. This enables a variety of downstream tasks, including hyperparameter marginalisation and Bayesian optimisation.

Deep Neural Networks as Point Estimates for Deep Gaussian Processes

Deep Gaussian processes (DGPs) have struggled for relevance in applications due to the challenges and cost associated with Bayesian inference. In this paper we propose a sparse variational approximation for DGPs for which the approximate posterior mean has the same mathematical structure as a Deep Neural Network (DNN). We make the forward pass through a DGP equivalent to a ReLU DNN by finding an interdomain transformation that represents the GP posterior mean as a sum of ReLU basis functions. This unification enables the initialisation and training of the DGP as a neural network, leveraging the well established practice in the deep learning community, and so greatly aiding the inference task. The experiments demonstrate improved accuracy and faster training compared to current DGP methods, while retaining favourable predictive uncertainties.

GPflux: A Library for Deep Gaussian Processes

We introduce GPflux, a Python library for Bayesian deep learning with a strong emphasis on deep Gaussian processes (DGPs). Implementing DGPs is a challenging endeavour due to the various mathematical subtleties that arise when dealing with multivariate Gaussian distributions and the complex bookkeeping of indices. To date, there are no actively maintained, open-sourced and extendable libraries available that support research activities in this area. GPflux aims to fill this gap by providing a library with state-of-the-art DGP algorithms, as well as building blocks for implementing novel Bayesian and GP-based hierarchical models and inference schemes. GPflux is compatible with and built on top of the Keras deep learning eco-system. This enables practitioners to leverage tools from the deep learning community for building and training customised Bayesian models, and create hierarchical models that consist of Bayesian and standard neural network layers in a single coherent framework. GPflux relies on GPflow for most of its GP objects and operations, which makes it an efficient, modular and extensible library, while having a lean codebase.

A Tutorial on Sparse Gaussian Processes and Variational Inference

Gaussian processes (GPs) provide a framework for Bayesian inference that can offer principled uncertainty estimates for a large range of problems. For example, if we consider regression problems with Gaussian likelihoods, a GP model enjoys a posterior in closed form. However, identifying the posterior GP scales cubically with the number of training examples and requires to store all examples in memory. In order to overcome these obstacles, sparse GPs have been proposed that approximate the true posterior GP with pseudo-training examples. Importantly, the number of pseudo-training examples is user-defined and enables control over computational and memory complexity. In the general case, sparse GPs do not enjoy closed-form solutions and one has to resort to approximate inference. In this context, a convenient choice for approximate inference is variational inference (VI), where the problem of Bayesian inference is cast as an optimization problem -- namely, to maximize a lower bound of the log marginal likelihood. This paves the way for a powerful and versatile framework, where pseudo-training examples are treated as optimization arguments of the approximate posterior that are jointly identified together with hyperparameters of the generative model (i.e. prior and likelihood). The framework can naturally handle a wide scope of supervised learning problems, ranging from regression with heteroscedastic and non-Gaussian likelihoods to classification problems with discrete labels, but also multilabel problems. The purpose of this tutorial is to provide access to the basic matter for readers without prior knowledge in both GPs and VI. A proper exposition to the subject enables also access to more recent advances (like importance-weighted VI as well as inderdomain, multioutput and deep GPs) that can serve as an inspiration for new research ideas.