No-Regret Thompson Sampling for Finite-Horizon Markov Decision Processes with Gaussian Processes

Thompson sampling (TS) is a powerful and widely used strategy for sequential decision-making, with applications ranging from Bayesian optimization to reinforcement learning (RL). Despite its success, the theoretical foundations of TS remain limited, particularly in settings with complex temporal structure such as RL. We address this gap by establishing no-regret guarantees for TS using models with Gaussian marginal distributions. Specifically, we consider TS in episodic RL with joint Gaussian process (GP) priors over rewards and transitions. We prove a regret bound of $\mathcal{\tilde{O}}(\sqrt{KH\Gamma(KH)})$ over $K$ episodes of horizon $H$, where $\Gamma(\cdot)$ captures the complexity of the GP model. Our analysis addresses several challenges, including the non-Gaussian nature of value functions and the recursive structure of Bellman updates, and extends classical tools such as the elliptical potential lemma to multi-output settings. This work advances the understanding of TS in RL and highlights how structural assumptions and model uncertainty shape its performance in finite-horizon Markov Decision Processes.

Bayesian Nonparametric Dynamical Clustering of Time Series

We present a method that models the evolution of an unbounded number of time series clusters by switching among an unknown number of regimes with linear dynamics. We develop a Bayesian non-parametric approach using a hierarchical Dirichlet process as a prior on the parameters of a Switching Linear Dynamical System and a Gaussian process prior to model the statistical variations in amplitude and temporal alignment within each cluster. By modeling the evolution of time series patterns, the method avoids unnecessary proliferation of clusters in a principled manner. We perform inference by formulating a variational lower bound for off-line and on-line scenarios, enabling efficient learning through optimization. We illustrate the versatility and effectiveness of the approach through several case studies of electrocardiogram analysis using publicly available databases.

Calabi-Yau metrics through Grassmannian learning and Donaldson's algorithm

Motivated by recent progress in the problem of numerical K\"ahler metrics, we survey machine learning techniques in this area, discussing both advantages and drawbacks. We then revisit the algebraic ansatz pioneered by Donaldson. Inspired by his work, we present a novel approach to obtaining Ricci-flat approximations to K\"ahler metrics, applying machine learning within a `principled' framework. In particular, we use gradient descent on the Grassmannian manifold to identify an efficient subspace of sections for calculation of the metric. We combine this approach with both Donaldson's algorithm and learning on the $h$-matrix itself (the latter method being equivalent to gradient descent on the fibre bundle of Hermitian metrics on the tautological bundle over the Grassmannian). We implement our methods on the Dwork family of threefolds, commenting on the behaviour at different points in moduli space. In particular, we observe the emergence of nontrivial local minima as the moduli parameter is increased.

Variance reduction of diffusion model's gradients with Taylor approximation-based control variate

Score-based models, trained with denoising score matching, are remarkably effective in generating high dimensional data. However, the high variance of their training objective hinders optimisation. We attempt to reduce it with a control variate, derived via a $k$-th order Taylor expansion on the training objective and its gradient. We prove an equivalence between the two and demonstrate empirically the effectiveness of our approach on a low dimensional problem setting; and study its effect on larger problems.

Linear combinations of latents in diffusion models: interpolation and beyond

Generative models are crucial for applications like data synthesis and augmentation. Diffusion, Flow Matching and Continuous Normalizing Flows have shown effectiveness across various modalities, and rely on Gaussian latent variables for generation. As any generated object is directly associated with a particular latent variable, we can manipulate the variables to exert control over the generation process. However, standard approaches for combining latent variables, such as spherical interpolation, only apply or work well in special cases. Moreover, current methods for obtaining low-dimensional representations of the data, important for e.g. surrogate models for search and creative applications, are network and data modality specific. In this work we show that the standard methods to combine variables do not yield intermediates following the distribution the models are trained to expect. We propose Combination of Gaussian variables (COG), a novel interpolation method that addresses this, is easy to implement yet matches or improves upon current methods. COG addresses linear combinations in general and, as we demonstrate, also supports other operations including e.g. defining subspaces of the latent space, simplifying the creation of expressive low-dimensional spaces of high-dimensional objects using generative models based on Gaussian latents.

Reparameterization invariance in approximate Bayesian inference

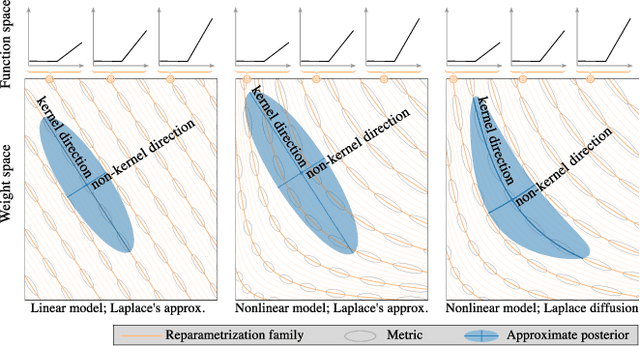
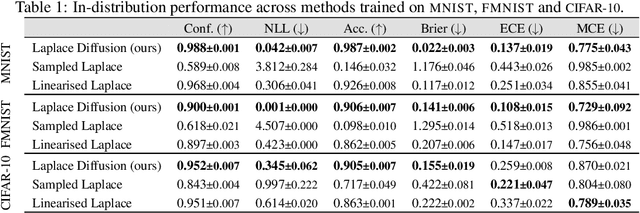
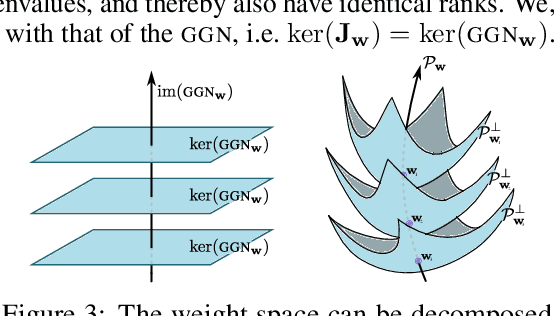
Current approximate posteriors in Bayesian neural networks (BNNs) exhibit a crucial limitation: they fail to maintain invariance under reparameterization, i.e. BNNs assign different posterior densities to different parametrizations of identical functions. This creates a fundamental flaw in the application of Bayesian principles as it breaks the correspondence between uncertainty over the parameters with uncertainty over the parametrized function. In this paper, we investigate this issue in the context of the increasingly popular linearized Laplace approximation. Specifically, it has been observed that linearized predictives alleviate the common underfitting problems of the Laplace approximation. We develop a new geometric view of reparametrizations from which we explain the success of linearization. Moreover, we demonstrate that these reparameterization invariance properties can be extended to the original neural network predictive using a Riemannian diffusion process giving a straightforward algorithm for approximate posterior sampling, which empirically improves posterior fit.

Identifying latent distances with Finslerian geometry

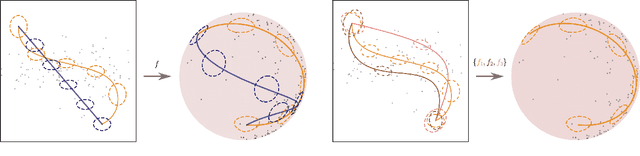
Riemannian geometry provides powerful tools to explore the latent space of generative models while preserving the inherent structure of the data manifold. Lengths, energies and volume measures can be derived from a pullback metric, defined through the immersion that maps the latent space to the data space. With this in mind, most generative models are stochastic, and so is the pullback metric. Manipulating stochastic objects is strenuous in practice. In order to perform operations such as interpolations, or measuring the distance between data points, we need a deterministic approximation of the pullback metric. In this work, we are defining a new metric as the expected length derived from the stochastic pullback metric. We show this metric is Finslerian, and we compare it with the expected pullback metric. In high dimensions, we show that the metrics converge to each other at a rate of $\mathcal{O}\left(\frac{1}{D}\right)$.

Optimisation of a global climate model ensemble for prediction of extreme heat days

Adaptation-relevant predictions of climate change are often derived by combining climate models in a multi-model ensemble. Model evaluation methods used in performance-based ensemble weighting schemes have limitations in the context of high-impact extreme events. We introduce a locally time-invariant model evaluation method with focus on assessing the simulation of extremes. We explore the behaviour of the proposed method in predicting extreme heat days in Nairobi.

Aligned Multi-Task Gaussian Process

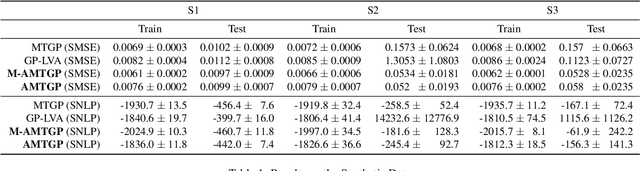
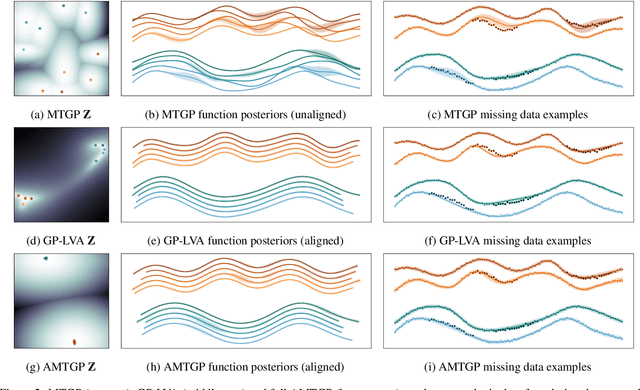
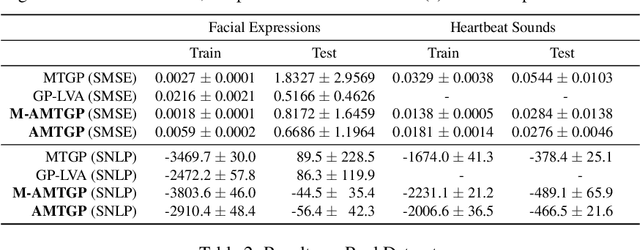
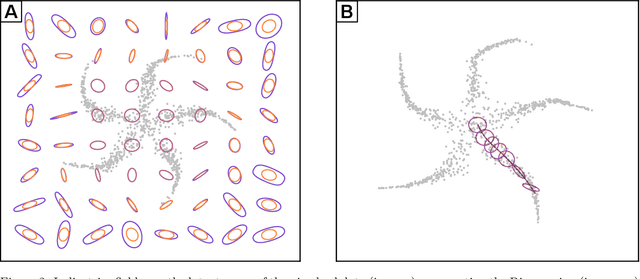
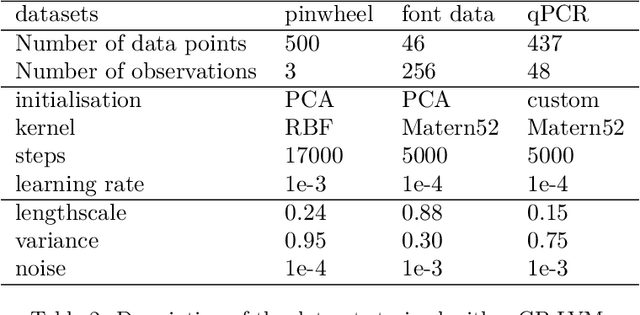
Multi-task learning requires accurate identification of the correlations between tasks. In real-world time-series, tasks are rarely perfectly temporally aligned; traditional multi-task models do not account for this and subsequent errors in correlation estimation will result in poor predictive performance and uncertainty quantification. We introduce a method that automatically accounts for temporal misalignment in a unified generative model that improves predictive performance. Our method uses Gaussian processes (GPs) to model the correlations both within and between the tasks. Building on the previous work by Kazlauskaiteet al. [2019], we include a separate monotonic warp of the input data to model temporal misalignment. In contrast to previous work, we formulate a lower bound that accounts for uncertainty in both the estimates of the warping process and the underlying functions. Also, our new take on a monotonic stochastic process, with efficient path-wise sampling for the warp functions, allows us to perform full Bayesian inference in the model rather than MAP estimates. Missing data experiments, on synthetic and real time-series, demonstrate the advantages of accounting for misalignments (vs standard unaligned method) as well as modelling the uncertainty in the warping process(vs baseline MAP alignment approach).

Deep Neural Networks as Point Estimates for Deep Gaussian Processes

Deep Gaussian processes (DGPs) have struggled for relevance in applications due to the challenges and cost associated with Bayesian inference. In this paper we propose a sparse variational approximation for DGPs for which the approximate posterior mean has the same mathematical structure as a Deep Neural Network (DNN). We make the forward pass through a DGP equivalent to a ReLU DNN by finding an interdomain transformation that represents the GP posterior mean as a sum of ReLU basis functions. This unification enables the initialisation and training of the DGP as a neural network, leveraging the well established practice in the deep learning community, and so greatly aiding the inference task. The experiments demonstrate improved accuracy and faster training compared to current DGP methods, while retaining favourable predictive uncertainties.