Bayesian nonparametric shared multi-sequence time series segmentation
Paper and Code
Jan 27, 2020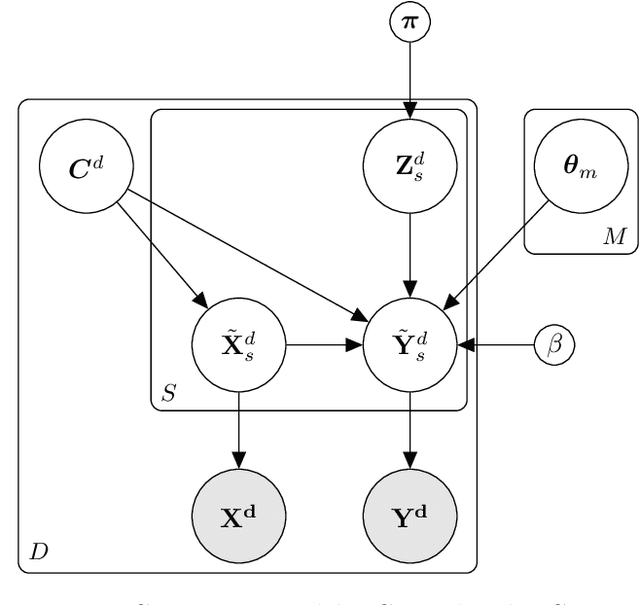
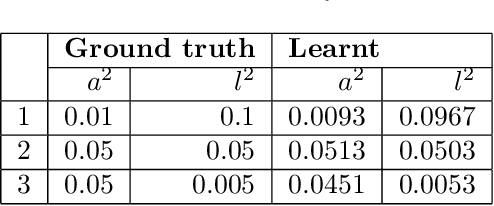
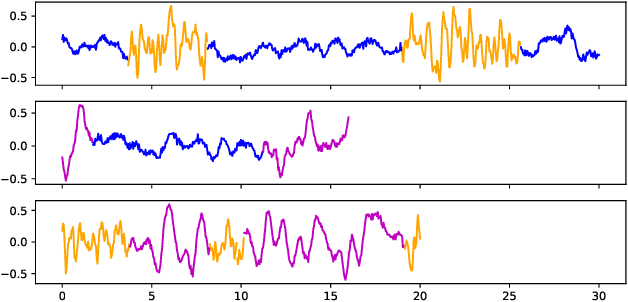
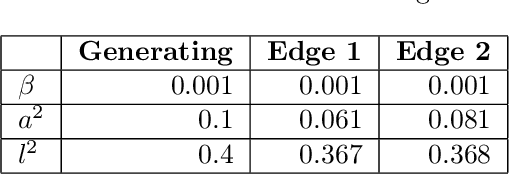
In this paper, we introduce a method for segmenting time series data using tools from Bayesian nonparametrics. We consider the task of temporal segmentation of a set of time series data into representative stationary segments. We use Gaussian process (GP) priors to impose our knowledge about the characteristics of the underlying stationary segments, and use a nonparametric distribution to partition the sequences into such segments, formulated in terms of a prior distribution on segment length. Given the segmentation, the model can be viewed as a variant of a Gaussian mixture model where the mixture components are described using the covariance function of a GP. We demonstrate the effectiveness of our model on synthetic data as well as on real time-series data of heartbeats where the task is to segment the indicative types of beats and to classify the heartbeat recordings into classes that correspond to healthy and abnormal heart sounds.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge