A Primer on Variational Inference for Physics-Informed Deep Generative Modelling

Variational inference (VI) is a computationally efficient and scalable methodology for approximate Bayesian inference. It strikes a balance between accuracy of uncertainty quantification and practical tractability. It excels at generative modelling and inversion tasks due to its built-in Bayesian regularisation and flexibility, essential qualities for physics related problems. Deriving the central learning objective for VI must often be tailored to new learning tasks where the nature of the problems dictates the conditional dependence between variables of interest, such as arising in physics problems. In this paper, we provide an accessible and thorough technical introduction to VI for forward and inverse problems, guiding the reader through standard derivations of the VI framework and how it can best be realized through deep learning. We then review and unify recent literature exemplifying the creative flexibility allowed by VI. This paper is designed for a general scientific audience looking to solve physics-based problems with an emphasis on uncertainty quantification.

Variational Bayesian surrogate modelling with application to robust design optimisation

Surrogate models provide a quick-to-evaluate approximation to complex computational models and are essential for multi-query problems like design optimisation. The inputs of current computational models are usually high-dimensional and uncertain. We consider Bayesian inference for constructing statistical surrogates with input uncertainties and intrinsic dimensionality reduction. The surrogates are trained by fitting to data from prevalent deterministic computational models. The assumed prior probability density of the surrogate is a Gaussian process. We determine the respective posterior probability density and parameters of the posited statistical model using variational Bayes. The non-Gaussian posterior is approximated by a simpler trial density with free variational parameters and the discrepancy between them is measured using the Kullback-Leibler (KL) divergence. We employ the stochastic gradient method to compute the variational parameters and other statistical model parameters by minimising the KL divergence. We demonstrate the accuracy and versatility of the proposed reduced dimension variational Gaussian process (RDVGP) surrogate on illustrative and robust structural optimisation problems with cost functions depending on a weighted sum of the mean and standard deviation of model outputs.

Random Grid Neural Processes for Parametric Partial Differential Equations

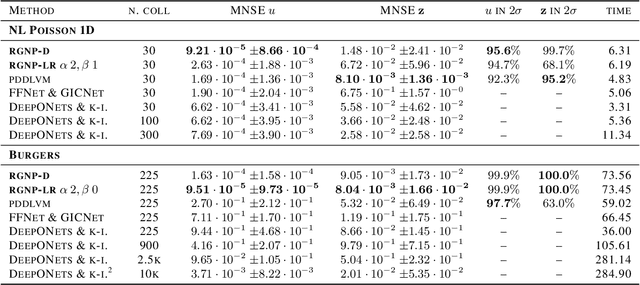
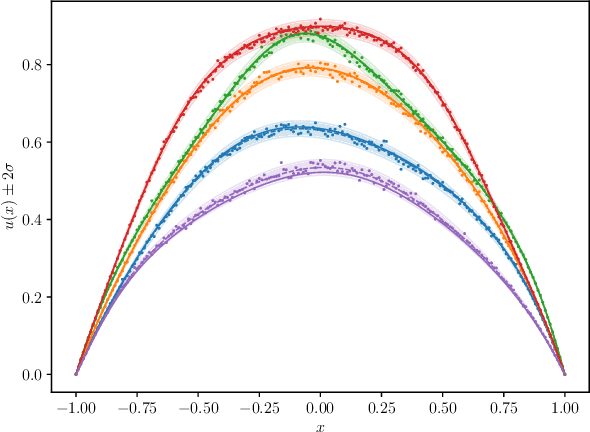
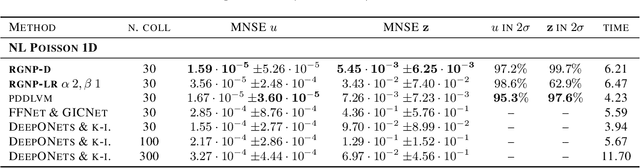
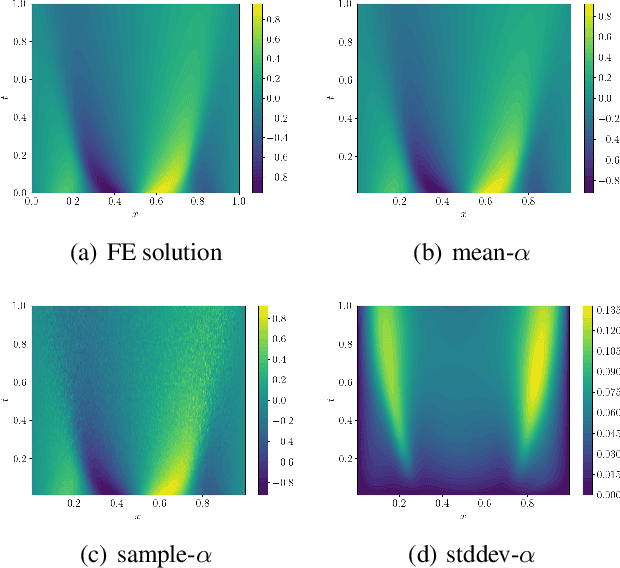
We introduce a new class of spatially stochastic physics and data informed deep latent models for parametric partial differential equations (PDEs) which operate through scalable variational neural processes. We achieve this by assigning probability measures to the spatial domain, which allows us to treat collocation grids probabilistically as random variables to be marginalised out. Adapting this spatial statistics view, we solve forward and inverse problems for parametric PDEs in a way that leads to the construction of Gaussian process models of solution fields. The implementation of these random grids poses a unique set of challenges for inverse physics informed deep learning frameworks and we propose a new architecture called Grid Invariant Convolutional Networks (GICNets) to overcome these challenges. We further show how to incorporate noisy data in a principled manner into our physics informed model to improve predictions for problems where data may be available but whose measurement location does not coincide with any fixed mesh or grid. The proposed method is tested on a nonlinear Poisson problem, Burgers equation, and Navier-Stokes equations, and we provide extensive numerical comparisons. We demonstrate significant computational advantages over current physics informed neural learning methods for parametric PDEs while improving the predictive capabilities and flexibility of these models.

Optimisation of a global climate model ensemble for prediction of extreme heat days

Adaptation-relevant predictions of climate change are often derived by combining climate models in a multi-model ensemble. Model evaluation methods used in performance-based ensemble weighting schemes have limitations in the context of high-impact extreme events. We introduce a locally time-invariant model evaluation method with focus on assessing the simulation of extremes. We explore the behaviour of the proposed method in predicting extreme heat days in Nairobi.

Ice Core Dating using Probabilistic Programming

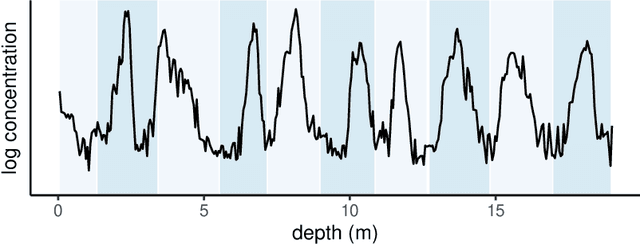
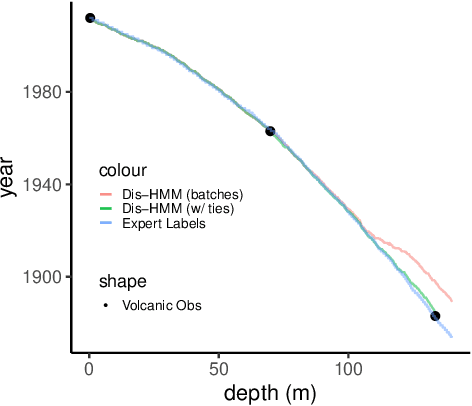
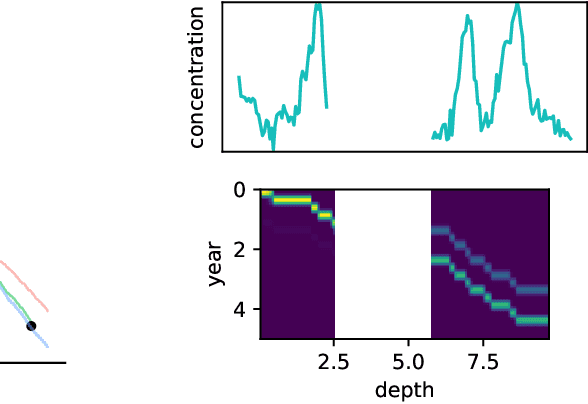
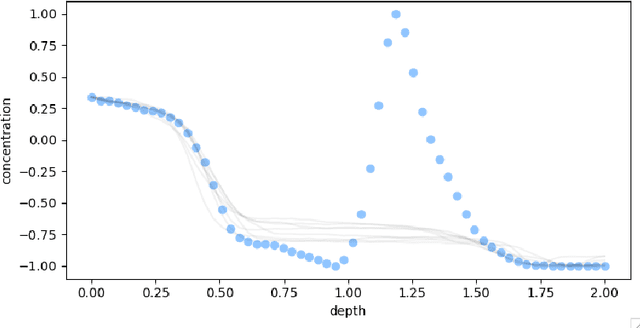
Ice cores record crucial information about past climate. However, before ice core data can have scientific value, the chronology must be inferred by estimating the age as a function of depth. Under certain conditions, chemicals locked in the ice display quasi-periodic cycles that delineate annual layers. Manually counting these noisy seasonal patterns to infer the chronology can be an imperfect and time-consuming process, and does not capture uncertainty in a principled fashion. In addition, several ice cores may be collected from a region, introducing an aspect of spatial correlation between them. We present an exploration of the use of probabilistic models for automatic dating of ice cores, using probabilistic programming to showcase its use for prototyping, automatic inference and maintainability, and demonstrate common failure modes of these tools.

Deep Probabilistic Models for Forward and Inverse Problems in Parametric PDEs

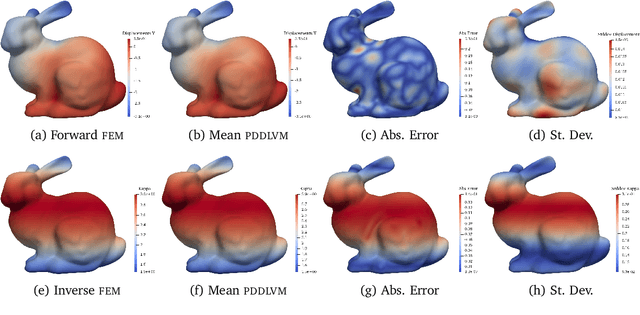
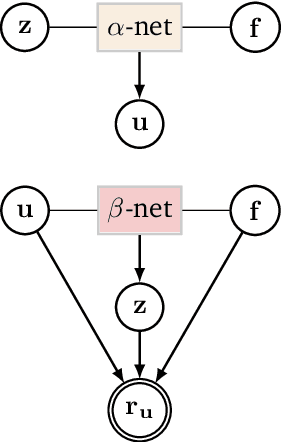
We formulate a class of physics-driven deep latent variable models (PDDLVM) to learn parameter-to-solution (forward) and solution-to-parameter (inverse) maps of parametric partial differential equations (PDEs). Our formulation leverages the finite element method (FEM), deep neural networks, and probabilistic modeling to assemble a deep probabilistic framework in which the forward and inverse maps are approximated with coherent uncertainty quantification. Our probabilistic model explicitly incorporates a parametric PDE-based density and a trainable solution-to-parameter network while the introduced amortized variational family postulates a parameter-to-solution network, all of which are jointly trained. Furthermore, the proposed methodology does not require any expensive PDE solves and is physics-informed only at training time, which allows real-time emulation of PDEs and generation of inverse problem solutions after training, bypassing the need for FEM solve operations with comparable accuracy to FEM solutions. The proposed framework further allows for a seamless integration of observed data for solving inverse problems and building generative models. We demonstrate the effectiveness of our method on a nonlinear Poisson problem, elastic shells with complex 3D geometries, and integrating generic physics-informed neural networks (PINN) architectures. We achieve up to three orders of magnitude speed-ups after training compared to traditional FEM solvers, while outputting coherent uncertainty estimates.

Aligned Multi-Task Gaussian Process

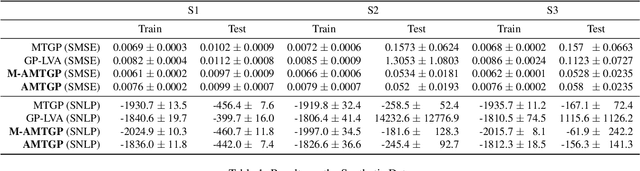
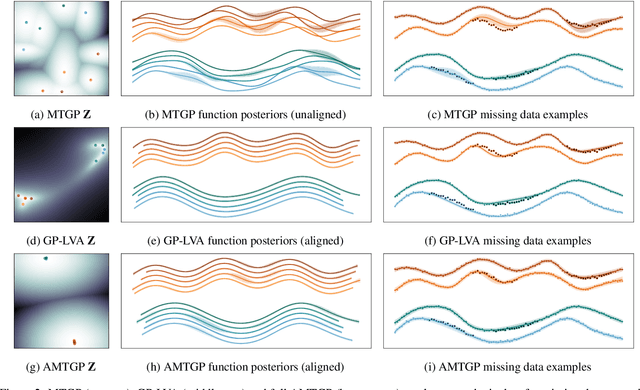
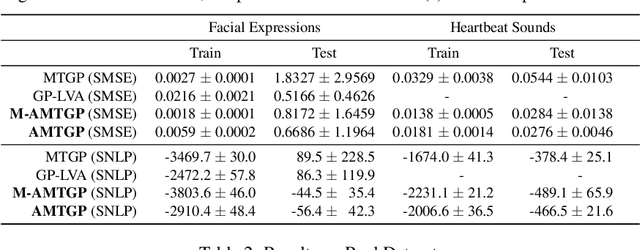
Multi-task learning requires accurate identification of the correlations between tasks. In real-world time-series, tasks are rarely perfectly temporally aligned; traditional multi-task models do not account for this and subsequent errors in correlation estimation will result in poor predictive performance and uncertainty quantification. We introduce a method that automatically accounts for temporal misalignment in a unified generative model that improves predictive performance. Our method uses Gaussian processes (GPs) to model the correlations both within and between the tasks. Building on the previous work by Kazlauskaiteet al. [2019], we include a separate monotonic warp of the input data to model temporal misalignment. In contrast to previous work, we formulate a lower bound that accounts for uncertainty in both the estimates of the warping process and the underlying functions. Also, our new take on a monotonic stochastic process, with efficient path-wise sampling for the warp functions, allows us to perform full Bayesian inference in the model rather than MAP estimates. Missing data experiments, on synthetic and real time-series, demonstrate the advantages of accounting for misalignments (vs standard unaligned method) as well as modelling the uncertainty in the warping process(vs baseline MAP alignment approach).

Bayesian nonparametric shared multi-sequence time series segmentation

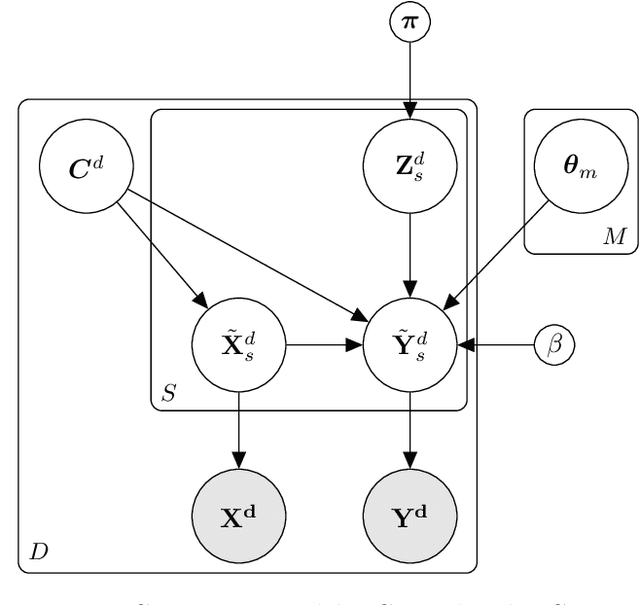
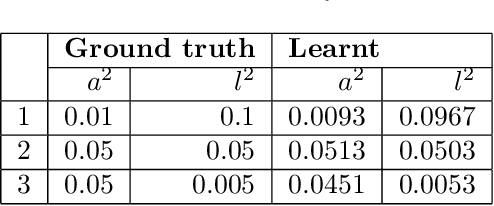
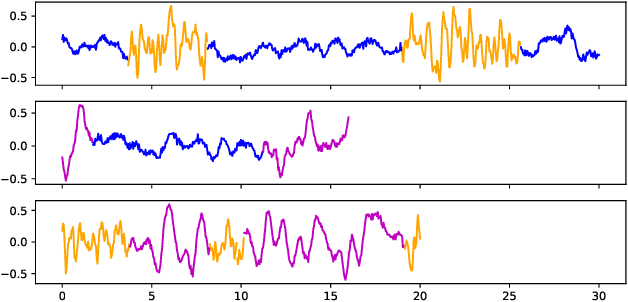
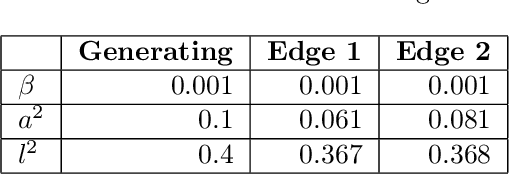
In this paper, we introduce a method for segmenting time series data using tools from Bayesian nonparametrics. We consider the task of temporal segmentation of a set of time series data into representative stationary segments. We use Gaussian process (GP) priors to impose our knowledge about the characteristics of the underlying stationary segments, and use a nonparametric distribution to partition the sequences into such segments, formulated in terms of a prior distribution on segment length. Given the segmentation, the model can be viewed as a variant of a Gaussian mixture model where the mixture components are described using the covariance function of a GP. We demonstrate the effectiveness of our model on synthetic data as well as on real time-series data of heartbeats where the task is to segment the indicative types of beats and to classify the heartbeat recordings into classes that correspond to healthy and abnormal heart sounds.

Compositional uncertainty in deep Gaussian processes

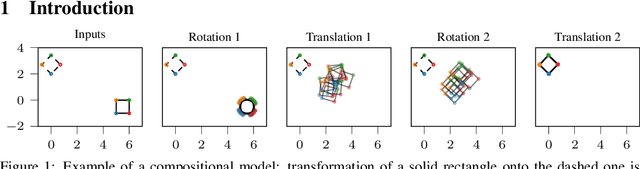
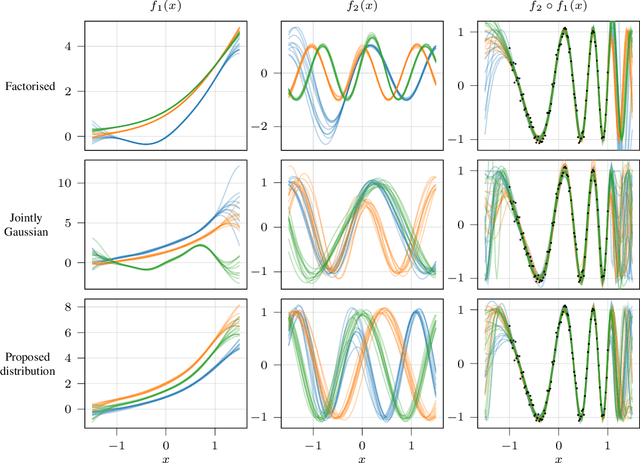
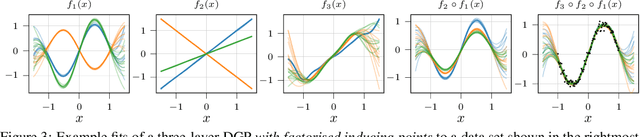
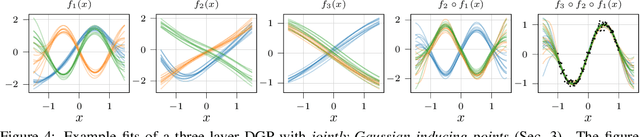
Gaussian processes (GPs) are nonparametric priors over functions, and fitting a GP to the data implies computing the posterior distribution of the functions consistent with the observed data. Similarly, deep Gaussian processes (DGPs) [Damianou:2013] should allow us to compute the posterior distribution of compositions of multiple functions giving rise to the observations. However, exact Bayesian inference is usually intractable for DGPs, motivating the use of various approximations. We show that the simplifying assumptions for a common type of Variational inference approximation imply that all but one layer of a DGP collapse to a deterministic transformation. We argue that such an inference scheme is suboptimal, not taking advantage of the potential of the model to discover the compositional structure in the data, and propose possible modifications addressing this issue.

Modulated Bayesian Optimization using Latent Gaussian Process Models

We present an approach to Bayesian Optimization that allows for robust search strategies over a large class of challenging functions. Our method is motivated by the belief that the trends useful to exploit in search of the optimum typically are a subset of the characteristics of the true objective function. At the core of our approach is the use of a Latent Gaussian Process Regression model that allows us to modulate the input domain with an orthogonal latent space. Using this latent space we can encapsulate local information about each observed data point that can be used to guide the search problem. We show experimentally that our method can be used to significantly improve performance on challenging benchmarks.