Efficient Deconvolution in Populational Inverse Problems

This work is focussed on the inversion task of inferring the distribution over parameters of interest leading to multiple sets of observations. The potential to solve such distributional inversion problems is driven by increasing availability of data, but a major roadblock is blind deconvolution, arising when the observational noise distribution is unknown. However, when data originates from collections of physical systems, a population, it is possible to leverage this information to perform deconvolution. To this end, we propose a methodology leveraging large data sets of observations, collected from different instantiations of the same physical processes, to simultaneously deconvolve the data corrupting noise distribution, and to identify the distribution over model parameters defining the physical processes. A parameter-dependent mathematical model of the physical process is employed. A loss function characterizing the match between the observed data and the output of the mathematical model is defined; it is minimized as a function of the both the parameter inputs to the model of the physics and the parameterized observational noise. This coupled problem is addressed with a modified gradient descent algorithm that leverages specific structure in the noise model. Furthermore, a new active learning scheme is proposed, based on adaptive empirical measures, to train a surrogate model to be accurate in parameter regions of interest; this approach accelerates computation and enables automatic differentiation of black-box, potentially nondifferentiable, code computing parameter-to-solution maps. The proposed methodology is demonstrated on porous medium flow, damped elastodynamics, and simplified models of atmospheric dynamics.

A Primer on Variational Inference for Physics-Informed Deep Generative Modelling

Variational inference (VI) is a computationally efficient and scalable methodology for approximate Bayesian inference. It strikes a balance between accuracy of uncertainty quantification and practical tractability. It excels at generative modelling and inversion tasks due to its built-in Bayesian regularisation and flexibility, essential qualities for physics related problems. Deriving the central learning objective for VI must often be tailored to new learning tasks where the nature of the problems dictates the conditional dependence between variables of interest, such as arising in physics problems. In this paper, we provide an accessible and thorough technical introduction to VI for forward and inverse problems, guiding the reader through standard derivations of the VI framework and how it can best be realized through deep learning. We then review and unify recent literature exemplifying the creative flexibility allowed by VI. This paper is designed for a general scientific audience looking to solve physics-based problems with an emphasis on uncertainty quantification.

Efficient Prior Calibration From Indirect Data

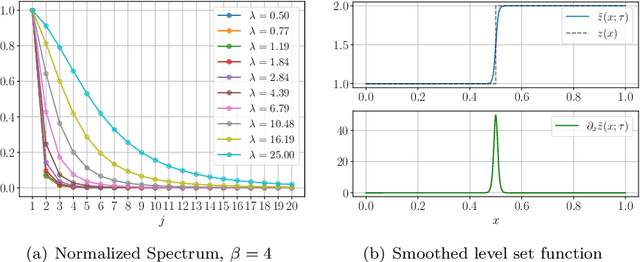
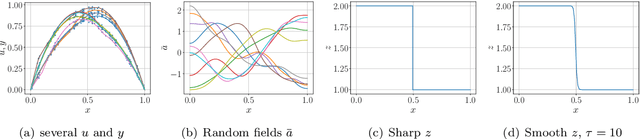
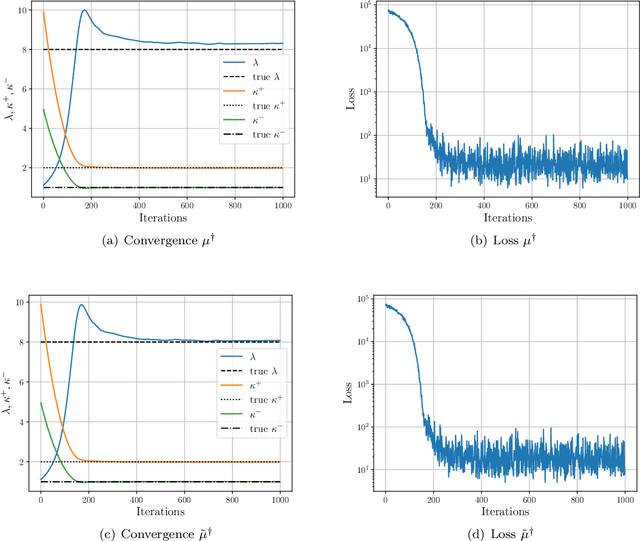
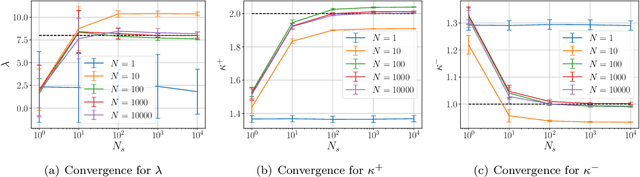
Bayesian inversion is central to the quantification of uncertainty within problems arising from numerous applications in science and engineering. To formulate the approach, four ingredients are required: a forward model mapping the unknown parameter to an element of a solution space, often the solution space for a differential equation; an observation operator mapping an element of the solution space to the data space; a noise model describing how noise pollutes the observations; and a prior model describing knowledge about the unknown parameter before the data is acquired. This paper is concerned with learning the prior model from data; in particular, learning the prior from multiple realizations of indirect data obtained through the noisy observation process. The prior is represented, using a generative model, as the pushforward of a Gaussian in a latent space; the pushforward map is learned by minimizing an appropriate loss function. A metric that is well-defined under empirical approximation is used to define the loss function for the pushforward map to make an implementable methodology. Furthermore, an efficient residual-based neural operator approximation of the forward model is proposed and it is shown that this may be learned concurrently with the pushforward map, using a bilevel optimization formulation of the problem; this use of neural operator approximation has the potential to make prior learning from indirect data more computationally efficient, especially when the observation process is expensive, non-smooth or not known. The ideas are illustrated with the Darcy flow inverse problem of finding permeability from piezometric head measurements.

Random Grid Neural Processes for Parametric Partial Differential Equations

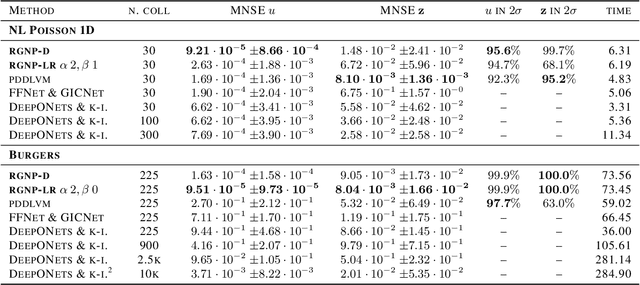
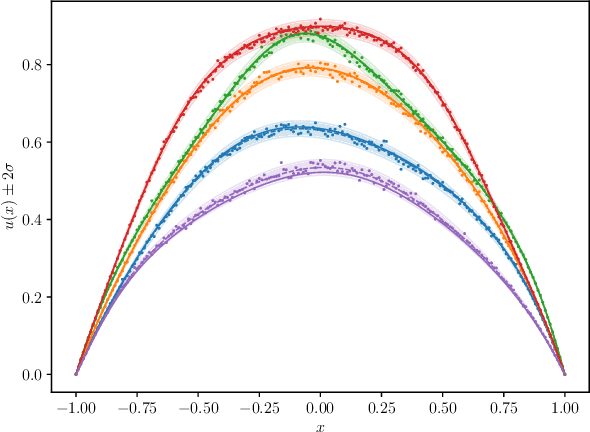
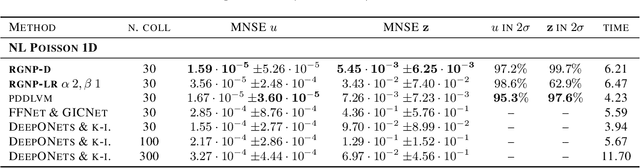
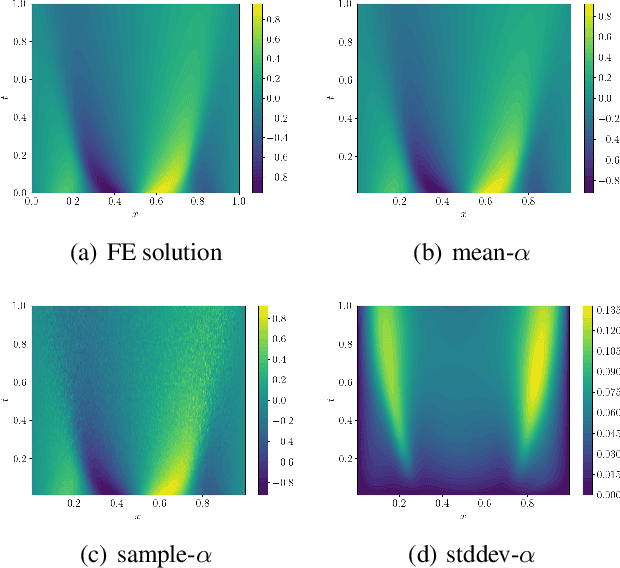
We introduce a new class of spatially stochastic physics and data informed deep latent models for parametric partial differential equations (PDEs) which operate through scalable variational neural processes. We achieve this by assigning probability measures to the spatial domain, which allows us to treat collocation grids probabilistically as random variables to be marginalised out. Adapting this spatial statistics view, we solve forward and inverse problems for parametric PDEs in a way that leads to the construction of Gaussian process models of solution fields. The implementation of these random grids poses a unique set of challenges for inverse physics informed deep learning frameworks and we propose a new architecture called Grid Invariant Convolutional Networks (GICNets) to overcome these challenges. We further show how to incorporate noisy data in a principled manner into our physics informed model to improve predictions for problems where data may be available but whose measurement location does not coincide with any fixed mesh or grid. The proposed method is tested on a nonlinear Poisson problem, Burgers equation, and Navier-Stokes equations, and we provide extensive numerical comparisons. We demonstrate significant computational advantages over current physics informed neural learning methods for parametric PDEs while improving the predictive capabilities and flexibility of these models.

Deep Probabilistic Models for Forward and Inverse Problems in Parametric PDEs

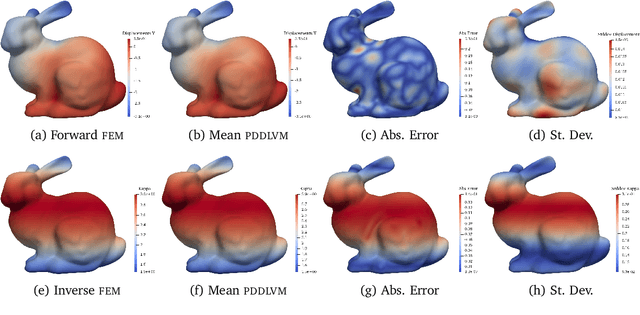
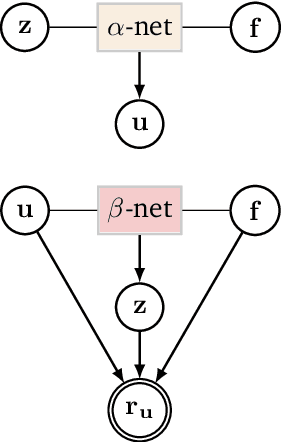
We formulate a class of physics-driven deep latent variable models (PDDLVM) to learn parameter-to-solution (forward) and solution-to-parameter (inverse) maps of parametric partial differential equations (PDEs). Our formulation leverages the finite element method (FEM), deep neural networks, and probabilistic modeling to assemble a deep probabilistic framework in which the forward and inverse maps are approximated with coherent uncertainty quantification. Our probabilistic model explicitly incorporates a parametric PDE-based density and a trainable solution-to-parameter network while the introduced amortized variational family postulates a parameter-to-solution network, all of which are jointly trained. Furthermore, the proposed methodology does not require any expensive PDE solves and is physics-informed only at training time, which allows real-time emulation of PDEs and generation of inverse problem solutions after training, bypassing the need for FEM solve operations with comparable accuracy to FEM solutions. The proposed framework further allows for a seamless integration of observed data for solving inverse problems and building generative models. We demonstrate the effectiveness of our method on a nonlinear Poisson problem, elastic shells with complex 3D geometries, and integrating generic physics-informed neural networks (PINN) architectures. We achieve up to three orders of magnitude speed-ups after training compared to traditional FEM solvers, while outputting coherent uncertainty estimates.