On diffusion-based generative models and their error bounds: The log-concave case with full convergence estimates

We provide full theoretical guarantees for the convergence behaviour of diffusion-based generative models under the assumption of strongly logconcave data distributions while our approximating class of functions used for score estimation is made of Lipschitz continuous functions. We demonstrate via a motivating example, sampling from a Gaussian distribution with unknown mean, the powerfulness of our approach. In this case, explicit estimates are provided for the associated optimization problem, i.e. score approximation, while these are combined with the corresponding sampling estimates. As a result, we obtain the best known upper bound estimates in terms of key quantities of interest, such as the dimension and rates of convergence, for the Wasserstein-2 distance between the data distribution (Gaussian with unknown mean) and our sampling algorithm. Beyond the motivating example and in order to allow for the use of a diverse range of stochastic optimizers, we present our results using an $L^2$-accurate score estimation assumption, which crucially is formed under an expectation with respect to the stochastic optimizer and our novel auxiliary process that uses only known information. This approach yields the best known convergence rate for our sampling algorithm.

Adaptively Optimised Adaptive Importance Samplers

We introduce a new class of adaptive importance samplers leveraging adaptive optimisation tools, which we term AdaOAIS. We build on Optimised Adaptive Importance Samplers (OAIS), a class of techniques that adapt proposals to improve the mean-squared error of the importance sampling estimators by parameterising the proposal and optimising the $\chi^2$-divergence between the target and the proposal. We show that a naive implementation of OAIS using stochastic gradient descent may lead to unstable estimators despite its convergence guarantees. To remedy this shortcoming, we instead propose to use adaptive optimisers (such as AdaGrad and Adam) to improve the stability of the OAIS. We provide convergence results for AdaOAIS in a similar manner to OAIS. We also provide empirical demonstration on a variety of examples and show that AdaOAIS lead to stable importance sampling estimators in practice.

Random Grid Neural Processes for Parametric Partial Differential Equations

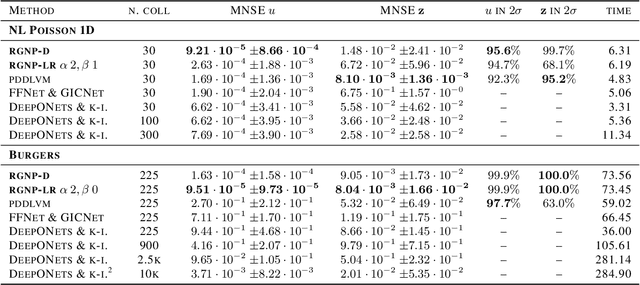
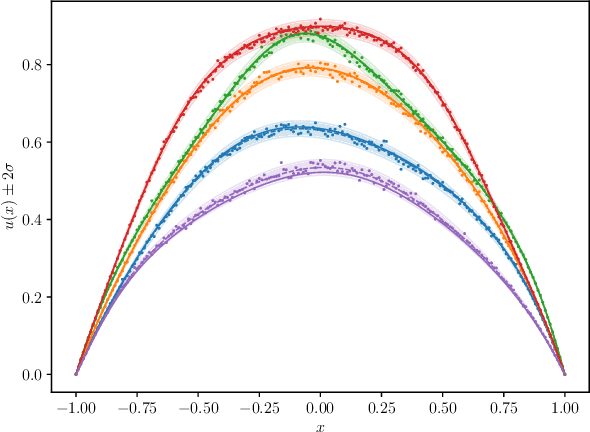
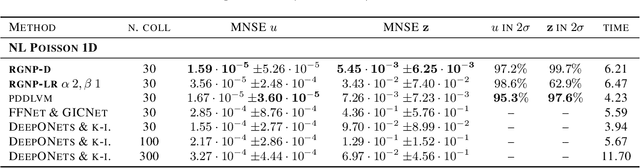
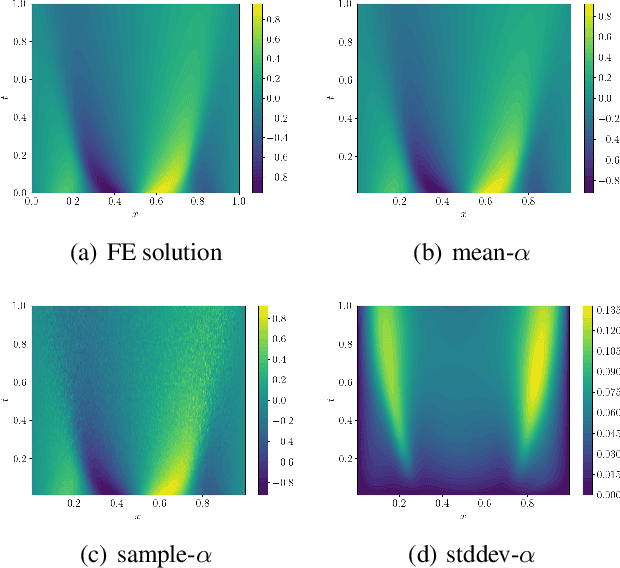
We introduce a new class of spatially stochastic physics and data informed deep latent models for parametric partial differential equations (PDEs) which operate through scalable variational neural processes. We achieve this by assigning probability measures to the spatial domain, which allows us to treat collocation grids probabilistically as random variables to be marginalised out. Adapting this spatial statistics view, we solve forward and inverse problems for parametric PDEs in a way that leads to the construction of Gaussian process models of solution fields. The implementation of these random grids poses a unique set of challenges for inverse physics informed deep learning frameworks and we propose a new architecture called Grid Invariant Convolutional Networks (GICNets) to overcome these challenges. We further show how to incorporate noisy data in a principled manner into our physics informed model to improve predictions for problems where data may be available but whose measurement location does not coincide with any fixed mesh or grid. The proposed method is tested on a nonlinear Poisson problem, Burgers equation, and Navier-Stokes equations, and we provide extensive numerical comparisons. We demonstrate significant computational advantages over current physics informed neural learning methods for parametric PDEs while improving the predictive capabilities and flexibility of these models.

Deep Probabilistic Models for Forward and Inverse Problems in Parametric PDEs

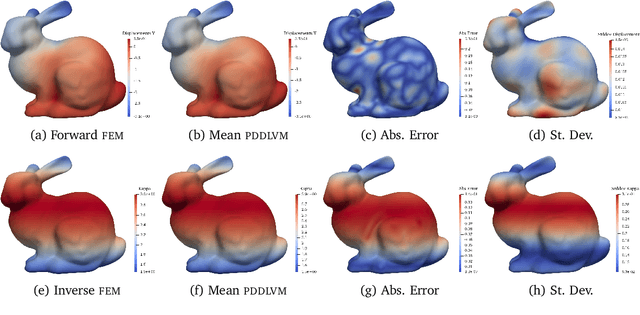
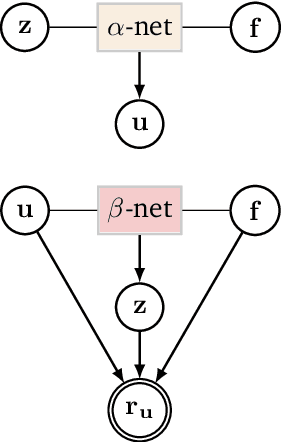
We formulate a class of physics-driven deep latent variable models (PDDLVM) to learn parameter-to-solution (forward) and solution-to-parameter (inverse) maps of parametric partial differential equations (PDEs). Our formulation leverages the finite element method (FEM), deep neural networks, and probabilistic modeling to assemble a deep probabilistic framework in which the forward and inverse maps are approximated with coherent uncertainty quantification. Our probabilistic model explicitly incorporates a parametric PDE-based density and a trainable solution-to-parameter network while the introduced amortized variational family postulates a parameter-to-solution network, all of which are jointly trained. Furthermore, the proposed methodology does not require any expensive PDE solves and is physics-informed only at training time, which allows real-time emulation of PDEs and generation of inverse problem solutions after training, bypassing the need for FEM solve operations with comparable accuracy to FEM solutions. The proposed framework further allows for a seamless integration of observed data for solving inverse problems and building generative models. We demonstrate the effectiveness of our method on a nonlinear Poisson problem, elastic shells with complex 3D geometries, and integrating generic physics-informed neural networks (PINN) architectures. We achieve up to three orders of magnitude speed-ups after training compared to traditional FEM solvers, while outputting coherent uncertainty estimates.

Global convergence of optimized adaptive importance samplers

We analyze the optimized adaptive importance sampler (OAIS) for performing Monte Carlo integration with general proposals. We leverage a classical result which shows that the bias and the mean-squared error (MSE) of the importance sampling scales with the $\chi^2$-divergence between the target and the proposal and develop a scheme which performs global optimization of $\chi^2$-divergence. While it is known that this quantity is convex for exponential family proposals, the case of the general proposals has been an open problem. We close this gap by utilizing stochastic gradient Langevin dynamics (SGLD) and its underdamped counterpart for the global optimization of $\chi^2$-divergence and derive nonasymptotic bounds for the MSE by leveraging recent results from non-convex optimization literature. The resulting AIS schemes have explicit theoretical guarantees uniform in the number of iterations.

Statistical Finite Elements via Langevin Dynamics

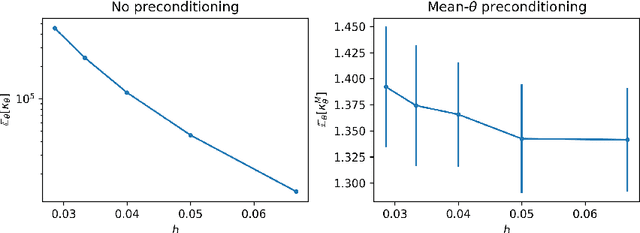
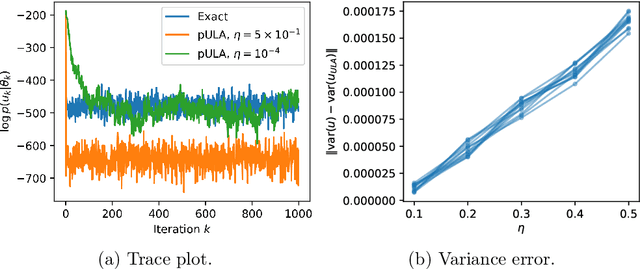
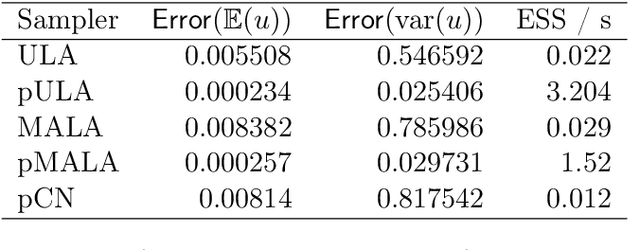
The recent statistical finite element method (statFEM) provides a coherent statistical framework to synthesise finite element models with observed data. Through embedding uncertainty inside of the governing equations, finite element solutions are updated to give a posterior distribution which quantifies all sources of uncertainty associated with the model. However to incorporate all sources of uncertainty, one must integrate over the uncertainty associated with the model parameters, the known forward problem of uncertainty quantification. In this paper, we make use of Langevin dynamics to solve the statFEM forward problem, studying the utility of the unadjusted Langevin algorithm (ULA), a Metropolis-free Markov chain Monte Carlo sampler, to build a sample-based characterisation of this otherwise intractable measure. Due to the structure of the statFEM problem, these methods are able to solve the forward problem without explicit full PDE solves, requiring only sparse matrix-vector products. ULA is also gradient-based, and hence provides a scalable approach up to high degrees-of-freedom. Leveraging the theory behind Langevin-based samplers, we provide theoretical guarantees on sampler performance, demonstrating convergence, for both the prior and posterior, in the Kullback-Leibler divergence, and, in Wasserstein-2, with further results on the effect of preconditioning. Numerical experiments are also provided, for both the prior and posterior, to demonstrate the efficacy of the sampler, with a Python package also included.

VarGrad: A Low-Variance Gradient Estimator for Variational Inference

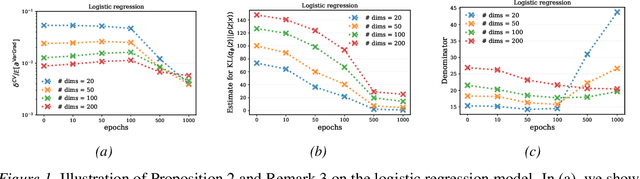
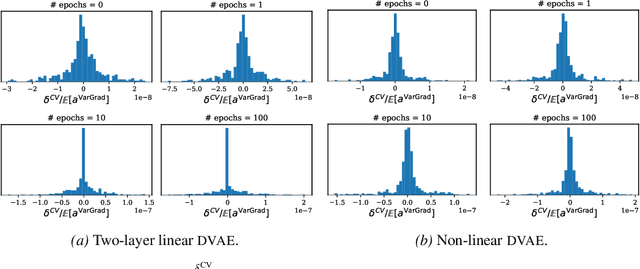
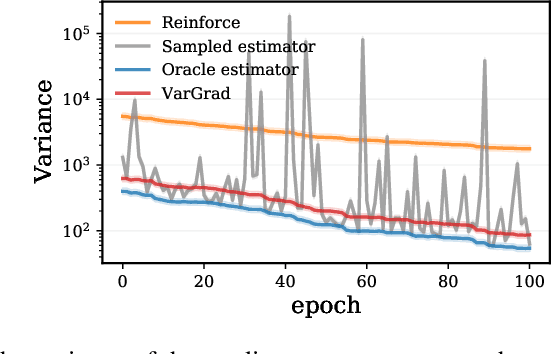
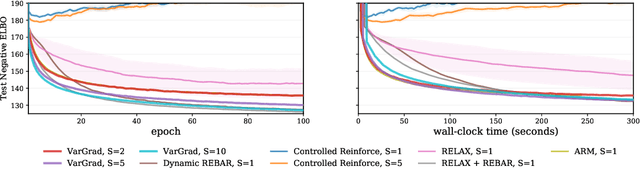
We analyse the properties of an unbiased gradient estimator of the ELBO for variational inference, based on the score function method with leave-one-out control variates. We show that this gradient estimator can be obtained using a new loss, defined as the variance of the log-ratio between the exact posterior and the variational approximation, which we call the $\textit{log-variance loss}$. Under certain conditions, the gradient of the log-variance loss equals the gradient of the (negative) ELBO. We show theoretically that this gradient estimator, which we call $\textit{VarGrad}$ due to its connection to the log-variance loss, exhibits lower variance than the score function method in certain settings, and that the leave-one-out control variate coefficients are close to the optimal ones. We empirically demonstrate that VarGrad offers a favourable variance versus computation trade-off compared to other state-of-the-art estimators on a discrete VAE.

Generalized Bayesian Filtering via Sequential Monte Carlo

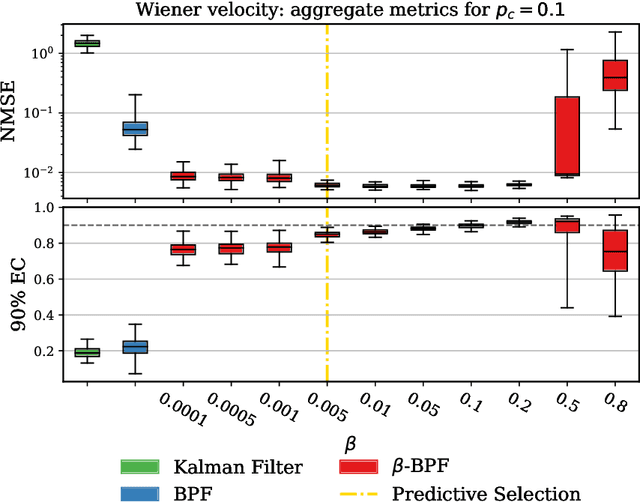
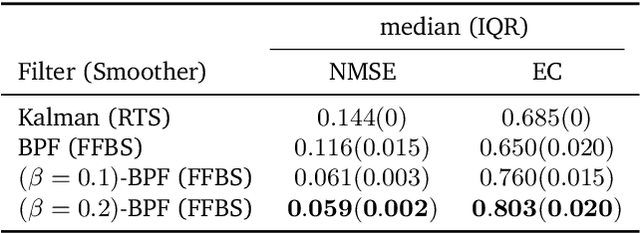
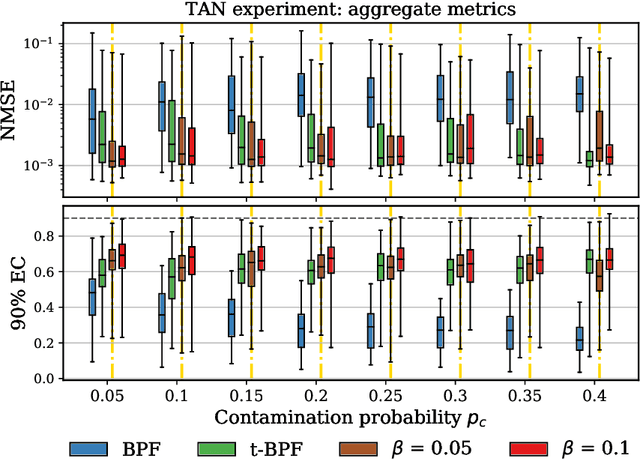
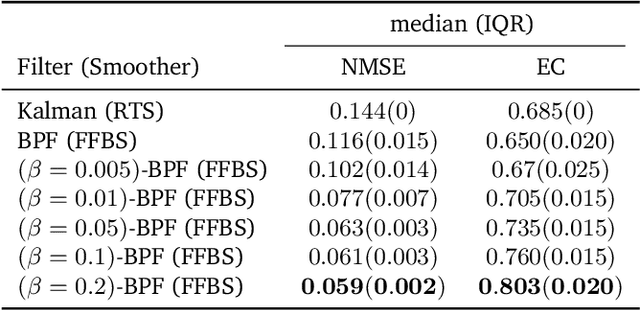
We introduce a framework for inference in general state-space hidden Markov models (HMMs) under likelihood misspecification. In particular, we leverage the loss-theoretic perspective of generalized Bayesian inference (GBI) to define generalized filtering recursions in HMMs, that can tackle the problem of inference under model misspecification. In doing so, we arrive at principled procedures for robust inference against observation contamination through the $\beta$-divergence. Operationalizing the proposed framework is made possible via sequential Monte Carlo methods (SMC). The standard particle methods, and their associated convergence results, are readily generalized to the new setting. We demonstrate our approach to object tracking and Gaussian process regression problems, and observe improved performance over standard filtering algorithms.

Nonasymptotic analysis of Stochastic Gradient Hamiltonian Monte Carlo under local conditions for nonconvex optimization

We provide a nonasymptotic analysis of the convergence of the stochastic gradient Hamiltonian Monte Carlo (SGHMC) to a target measure in Wasserstein-2 distance without assuming log-concavity. By making the dimension dependence explicit, we provide a uniform convergence rate of order $\mathcal{O}(\eta^{1/4} )$, where $\eta$ is the step-size. Our results shed light onto the performance of the SGHMC methods compared to their overdamped counterparts, e.g., stochastic gradient Langevin dynamics (SGLD). Furthermore, our results also imply that the SGHMC, when viewed as a nonconvex optimizer, converges to a global minimum with the best known rates.

Nonasymptotic estimates for Stochastic Gradient Langevin Dynamics under local conditions in nonconvex optimization

Within the context of empirical risk minimization, see Raginsky, Rakhlin, and Telgarsky (2017), we are concerned with a non-asymptotic analysis of sampling algorithms used in optimization. In particular, we obtain non-asymptotic error bounds for a popular class of algorithms called Stochastic Gradient Langevin Dynamics (SGLD). These results are derived in appropriate Wasserstein distances in the absence of the log-concavity of the target distribution. More precisely, the local Lipschitzness of the stochastic gradient $H(\theta, x)$ is assumed, and furthermore, the dissipativity and convexity at infinity condition are relaxed by removing the uniform dependence in $x$.