$Φ$-DVAE: Learning Physically Interpretable Representations with Nonlinear Filtering

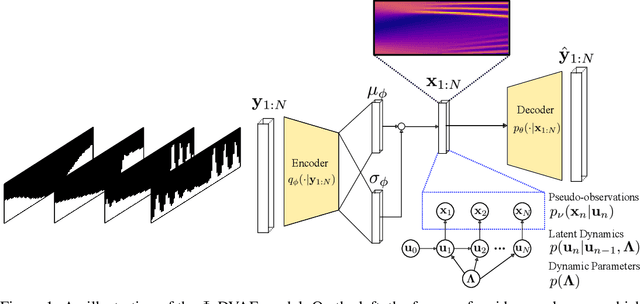
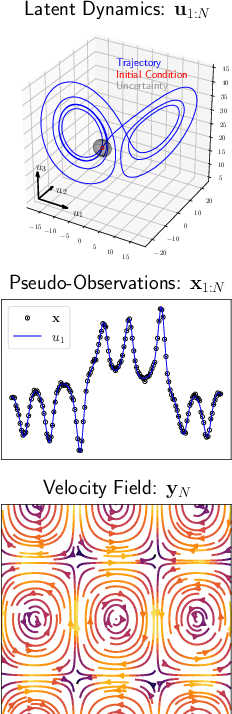
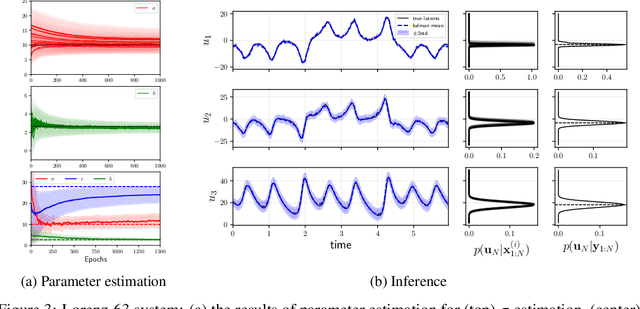
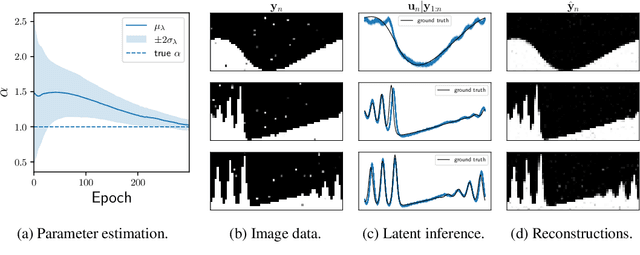
Incorporating unstructured data into physical models is a challenging problem that is emerging in data assimilation. Traditional approaches focus on well-defined observation operators whose functional forms are typically assumed to be known. This prevents these methods from achieving a consistent model-data synthesis in configurations where the mapping from data-space to model-space is unknown. To address these shortcomings, in this paper we develop a physics-informed dynamical variational autoencoder ($\Phi$-DVAE) for embedding diverse data streams into time-evolving physical systems described by differential equations. Our approach combines a standard (possibly nonlinear) filter for the latent state-space model and a VAE, to embed the unstructured data stream into the latent dynamical system. A variational Bayesian framework is used for the joint estimation of the embedding, latent states, and unknown system parameters. To demonstrate the method, we look at three examples: video datasets generated by the advection and Korteweg-de Vries partial differential equations, and a velocity field generated by the Lorenz-63 system. Comparisons with relevant baselines show that the $\Phi$-DVAE provides a data efficient dynamics encoding methodology that is competitive with standard approaches, with the added benefit of incorporating a physically interpretable latent space.

Statistical Finite Elements via Langevin Dynamics

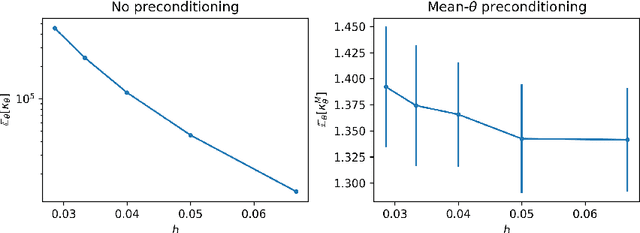
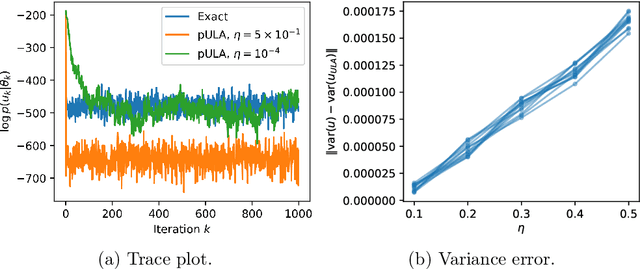
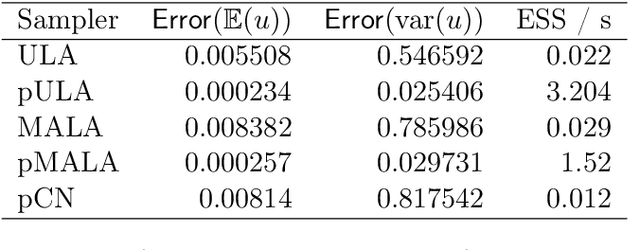
The recent statistical finite element method (statFEM) provides a coherent statistical framework to synthesise finite element models with observed data. Through embedding uncertainty inside of the governing equations, finite element solutions are updated to give a posterior distribution which quantifies all sources of uncertainty associated with the model. However to incorporate all sources of uncertainty, one must integrate over the uncertainty associated with the model parameters, the known forward problem of uncertainty quantification. In this paper, we make use of Langevin dynamics to solve the statFEM forward problem, studying the utility of the unadjusted Langevin algorithm (ULA), a Metropolis-free Markov chain Monte Carlo sampler, to build a sample-based characterisation of this otherwise intractable measure. Due to the structure of the statFEM problem, these methods are able to solve the forward problem without explicit full PDE solves, requiring only sparse matrix-vector products. ULA is also gradient-based, and hence provides a scalable approach up to high degrees-of-freedom. Leveraging the theory behind Langevin-based samplers, we provide theoretical guarantees on sampler performance, demonstrating convergence, for both the prior and posterior, in the Kullback-Leibler divergence, and, in Wasserstein-2, with further results on the effect of preconditioning. Numerical experiments are also provided, for both the prior and posterior, to demonstrate the efficacy of the sampler, with a Python package also included.

Low-rank statistical finite elements for scalable model-data synthesis

Statistical learning additions to physically derived mathematical models are gaining traction in the literature. A recent approach has been to augment the underlying physics of the governing equations with data driven Bayesian statistical methodology. Coined statFEM, the method acknowledges a priori model misspecification, by embedding stochastic forcing within the governing equations. Upon receipt of additional data, the posterior distribution of the discretised finite element solution is updated using classical Bayesian filtering techniques. The resultant posterior jointly quantifies uncertainty associated with the ubiquitous problem of model misspecification and the data intended to represent the true process of interest. Despite this appeal, computational scalability is a challenge to statFEM's application to high-dimensional problems typically experienced in physical and industrial contexts. This article overcomes this hurdle by embedding a low-rank approximation of the underlying dense covariance matrix, obtained from the leading order modes of the full-rank alternative. Demonstrated on a series of reaction-diffusion problems of increasing dimension, using experimental and simulated data, the method reconstructs the sparsely observed data-generating processes with minimal loss of information, in both posterior mean and the variance, paving the way for further integration of physical and probabilistic approaches to complex systems.