$Φ$-DVAE: Learning Physically Interpretable Representations with Nonlinear Filtering

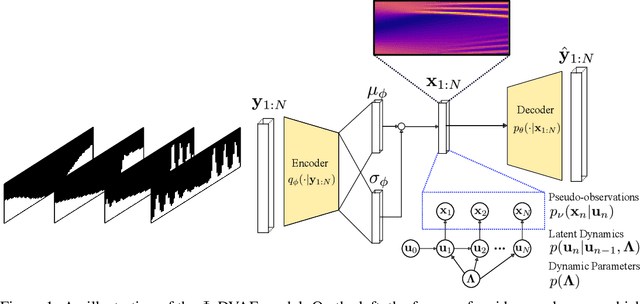
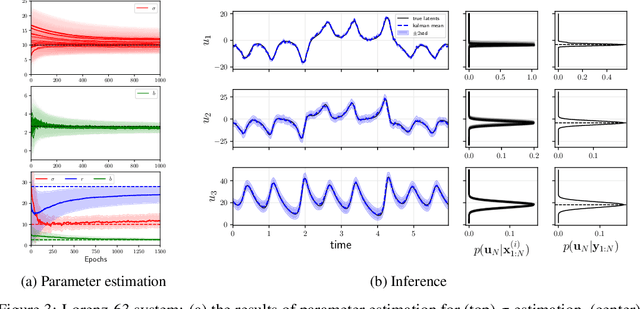
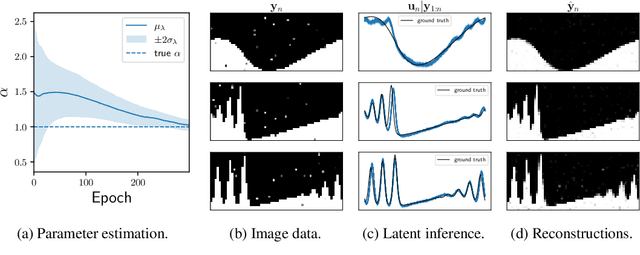
Incorporating unstructured data into physical models is a challenging problem that is emerging in data assimilation. Traditional approaches focus on well-defined observation operators whose functional forms are typically assumed to be known. This prevents these methods from achieving a consistent model-data synthesis in configurations where the mapping from data-space to model-space is unknown. To address these shortcomings, in this paper we develop a physics-informed dynamical variational autoencoder ($\Phi$-DVAE) for embedding diverse data streams into time-evolving physical systems described by differential equations. Our approach combines a standard (possibly nonlinear) filter for the latent state-space model and a VAE, to embed the unstructured data stream into the latent dynamical system. A variational Bayesian framework is used for the joint estimation of the embedding, latent states, and unknown system parameters. To demonstrate the method, we look at three examples: video datasets generated by the advection and Korteweg-de Vries partial differential equations, and a velocity field generated by the Lorenz-63 system. Comparisons with relevant baselines show that the $\Phi$-DVAE provides a data efficient dynamics encoding methodology that is competitive with standard approaches, with the added benefit of incorporating a physically interpretable latent space.