Hierarchical Inference and Closure Learning via Adaptive Surrogates for ODEs and PDEs

Inverse problems are the task of calibrating models to match data. They play a pivotal role in diverse engineering applications by allowing practitioners to align models with reality. In many applications, engineers and scientists do not have a complete picture of i) the detailed properties of a system (such as material properties, geometry, initial conditions, etc.); ii) the complete laws describing all dynamics at play (such as friction laws, complicated damping phenomena, and general nonlinear interactions). In this paper, we develop a principled methodology for leveraging data from collections of distinct yet related physical systems to jointly estimate the individual model parameters of each system, and learn the shared unknown dynamics in the form of an ML-based closure model. To robustly infer the unknown parameters for each system, we employ a hierarchical Bayesian framework, which allows for the joint inference of multiple systems and their population-level statistics. To learn the closures, we use a maximum marginal likelihood estimate of a neural network embeded within the ODE/PDE formulation of the problem. To realize this framework we utilize the ensemble Metropolis-Adjusted Langevin Algorithm (MALA) for stable and efficient sampling. To mitigate the computational bottleneck of repetitive forward evaluations in solving inverse problems, we introduce a bilevel optimization strategy to simultaneously train a surrogate forward model alongside the inference. Within this framework, we evaluate and compare distinct surrogate architectures, specifically Fourier Neural Operators (FNO) and parametric Physics-Informed Neural Network (PINNs).

A Primer on Variational Inference for Physics-Informed Deep Generative Modelling

Variational inference (VI) is a computationally efficient and scalable methodology for approximate Bayesian inference. It strikes a balance between accuracy of uncertainty quantification and practical tractability. It excels at generative modelling and inversion tasks due to its built-in Bayesian regularisation and flexibility, essential qualities for physics related problems. Deriving the central learning objective for VI must often be tailored to new learning tasks where the nature of the problems dictates the conditional dependence between variables of interest, such as arising in physics problems. In this paper, we provide an accessible and thorough technical introduction to VI for forward and inverse problems, guiding the reader through standard derivations of the VI framework and how it can best be realized through deep learning. We then review and unify recent literature exemplifying the creative flexibility allowed by VI. This paper is designed for a general scientific audience looking to solve physics-based problems with an emphasis on uncertainty quantification.

$Φ$-DVAE: Learning Physically Interpretable Representations with Nonlinear Filtering

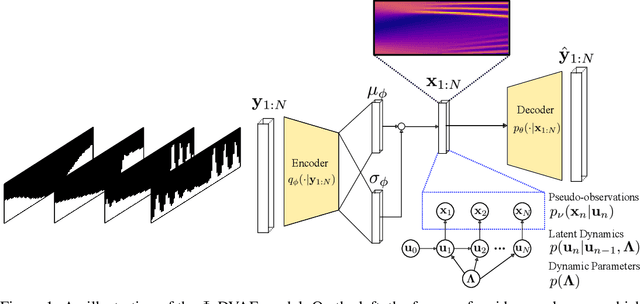
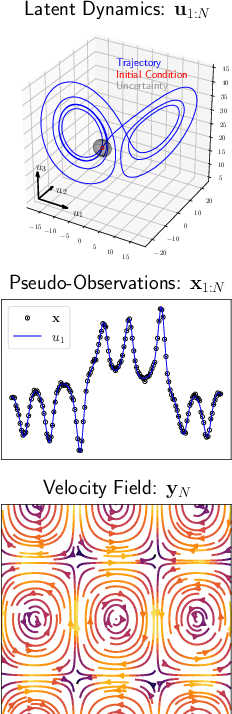
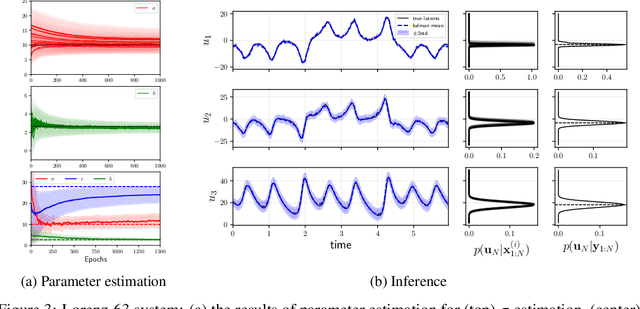
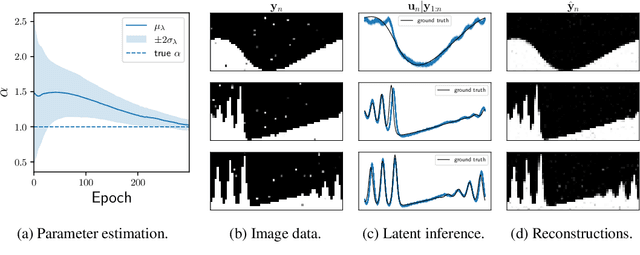
Incorporating unstructured data into physical models is a challenging problem that is emerging in data assimilation. Traditional approaches focus on well-defined observation operators whose functional forms are typically assumed to be known. This prevents these methods from achieving a consistent model-data synthesis in configurations where the mapping from data-space to model-space is unknown. To address these shortcomings, in this paper we develop a physics-informed dynamical variational autoencoder ($\Phi$-DVAE) for embedding diverse data streams into time-evolving physical systems described by differential equations. Our approach combines a standard (possibly nonlinear) filter for the latent state-space model and a VAE, to embed the unstructured data stream into the latent dynamical system. A variational Bayesian framework is used for the joint estimation of the embedding, latent states, and unknown system parameters. To demonstrate the method, we look at three examples: video datasets generated by the advection and Korteweg-de Vries partial differential equations, and a velocity field generated by the Lorenz-63 system. Comparisons with relevant baselines show that the $\Phi$-DVAE provides a data efficient dynamics encoding methodology that is competitive with standard approaches, with the added benefit of incorporating a physically interpretable latent space.