O. Deniz Akyildiz
Uniform-in-time convergence bounds for Persistent Contrastive Divergence Algorithms
Oct 02, 2025Abstract:We propose a continuous-time formulation of persistent contrastive divergence (PCD) for maximum likelihood estimation (MLE) of unnormalised densities. Our approach expresses PCD as a coupled, multiscale system of stochastic differential equations (SDEs), which perform optimisation of the parameter and sampling of the associated parametrised density, simultaneously. From this novel formulation, we are able to derive explicit bounds for the error between the PCD iterates and the MLE solution for the model parameter. This is made possible by deriving uniform-in-time (UiT) bounds for the difference in moments between the multiscale system and the averaged regime. An efficient implementation of the continuous-time scheme is introduced, leveraging a class of explicit, stable intregators, stochastic orthogonal Runge-Kutta Chebyshev (S-ROCK), for which we provide explicit error estimates in the long-time regime. This leads to a novel method for training energy-based models (EBMs) with explicit error guarantees.
Sampling by averaging: A multiscale approach to score estimation
Aug 20, 2025Abstract:We introduce a novel framework for efficient sampling from complex, unnormalised target distributions by exploiting multiscale dynamics. Traditional score-based sampling methods either rely on learned approximations of the score function or involve computationally expensive nested Markov chain Monte Carlo (MCMC) loops. In contrast, the proposed approach leverages stochastic averaging within a slow-fast system of stochastic differential equations (SDEs) to estimate intermediate scores along a diffusion path without training or inner-loop MCMC. Two algorithms are developed under this framework: MultALMC, which uses multiscale annealed Langevin dynamics, and MultCDiff, based on multiscale controlled diffusions for the reverse-time Ornstein-Uhlenbeck process. Both overdamped and underdamped variants are considered, with theoretical guarantees of convergence to the desired diffusion path. The framework is extended to handle heavy-tailed target distributions using Student's t-based noise models and tailored fast-process dynamics. Empirical results across synthetic and real-world benchmarks, including multimodal and high-dimensional distributions, demonstrate that the proposed methods are competitive with existing samplers in terms of accuracy and efficiency, without the need for learned models.
Learning Latent Variable Models via Jarzynski-adjusted Langevin Algorithm
May 23, 2025Abstract:We utilise a sampler originating from nonequilibrium statistical mechanics, termed here Jarzynski-adjusted Langevin algorithm (JALA), to build statistical estimation methods in latent variable models. We achieve this by leveraging Jarzynski's equality and developing algorithms based on a weighted version of the unadjusted Langevin algorithm (ULA) with recursively updated weights. Adapting this for latent variable models, we develop a sequential Monte Carlo (SMC) method that provides the maximum marginal likelihood estimate of the parameters, termed JALA-EM. Under suitable regularity assumptions on the marginal likelihood, we provide a nonasymptotic analysis of the JALA-EM scheme implemented with stochastic gradient descent and show that it provably converges to the maximum marginal likelihood estimate. We demonstrate the performance of JALA-EM on a variety of latent variable models and show that it performs comparably to existing methods in terms of accuracy and computational efficiency. Importantly, the ability to recursively estimate marginal likelihoods - an uncommon feature among scalable methods - makes our approach particularly suited for model selection, which we validate through dedicated experiments.
Training Latent Diffusion Models with Interacting Particle Algorithms
May 18, 2025Abstract:We introduce a novel particle-based algorithm for end-to-end training of latent diffusion models. We reformulate the training task as minimizing a free energy functional and obtain a gradient flow that does so. By approximating the latter with a system of interacting particles, we obtain the algorithm, which we underpin it theoretically by providing error guarantees. The novel algorithm compares favorably in experiments with previous particle-based methods and variational inference analogues.
On the contraction properties of Sinkhorn semigroups
Mar 12, 2025Abstract:We develop a novel semigroup contraction analysis based on Lyapunov techniques to prove the exponential convergence of Sinkhorn equations on weighted Banach spaces. This operator-theoretic framework yields exponential decays of Sinkhorn iterates towards Schr\"odinger bridges with respect to general classes of $\phi$-divergences as well as in weighted Banach spaces. To the best of our knowledge, these are the first results of this type in the literature on entropic transport and the Sinkhorn algorithm. We also illustrate the impact of these results in the context of multivariate linear Gaussian models as well as statistical finite mixture models including Gaussian-kernel density estimation of complex data distributions arising in generative models.
Non-asymptotic Analysis of Diffusion Annealed Langevin Monte Carlo for Generative Modelling
Feb 13, 2025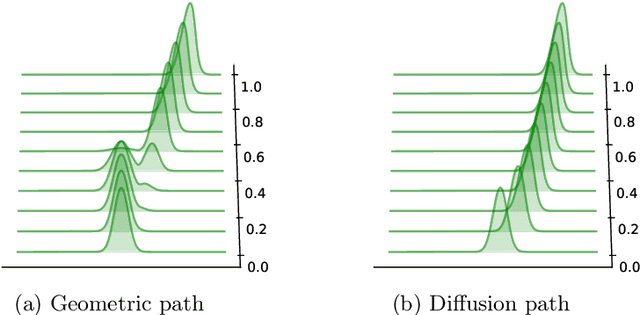
Abstract:We investigate the theoretical properties of general diffusion (interpolation) paths and their Langevin Monte Carlo implementation, referred to as diffusion annealed Langevin Monte Carlo (DALMC), under weak conditions on the data distribution. Specifically, we analyse and provide non-asymptotic error bounds for the annealed Langevin dynamics where the path of distributions is defined as Gaussian convolutions of the data distribution as in diffusion models. We then extend our results to recently proposed heavy-tailed (Student's t) diffusion paths, demonstrating their theoretical properties for heavy-tailed data distributions for the first time. Our analysis provides theoretical guarantees for a class of score-based generative models that interpolate between a simple distribution (Gaussian or Student's t) and the data distribution in finite time. This approach offers a broader perspective compared to standard score-based diffusion approaches, which are typically based on a forward Ornstein-Uhlenbeck (OU) noising process.
Gaussian entropic optimal transport: Schrödinger bridges and the Sinkhorn algorithm
Dec 24, 2024Abstract:Entropic optimal transport problems are regularized versions of optimal transport problems. These models play an increasingly important role in machine learning and generative modelling. For finite spaces, these problems are commonly solved using Sinkhorn algorithm (a.k.a. iterative proportional fitting procedure). However, in more general settings the Sinkhorn iterations are based on nonlinear conditional/conjugate transformations and exact finite-dimensional solutions cannot be computed. This article presents a finite-dimensional recursive formulation of the iterative proportional fitting procedure for general Gaussian multivariate models. As expected, this recursive formulation is closely related to the celebrated Kalman filter and related Riccati matrix difference equations, and it yields algorithms that can be implemented in practical settings without further approximations. We extend this filtering methodology to develop a refined and self-contained convergence analysis of Gaussian Sinkhorn algorithms, including closed form expressions of entropic transport maps and Schr\"odinger bridges.
On Diffusion Posterior Sampling via Sequential Monte Carlo for Zero-Shot Scaffolding of Protein Motifs
Dec 08, 2024Abstract:With the advent of diffusion models, new proteins can be generated at an unprecedented rate. The \textit{motif scaffolding problem} requires steering this generative process to yield proteins with a desirable functional substructure -- a motif. While models have been trained to take the motif as conditional input, recent techniques in diffusion posterior sampling can be leveraged as zero-shot alternatives whose approximations can be corrected with sequential Monte Carlo (SMC) algorithms. In this work, we introduce a new set of guidance potentials to describe and solve scaffolding tasks by adapting SMC-aided diffusion posterior samplers with an unconditional model, Genie, acting as a prior. Against established benchmarks, we successfully scaffold several single-motif and multi-motif problems. The latter is possible by pairing reconstruction guidance with $\mathrm{SE}(3)$-invariant potentials. In the single-motif case, we find these potentials perform comparably to the conventional masking approach and that reconstruction guidance outperforms replacement methods when aided with SMC. We additionally consider a guidance potential for point symmetry constraints and produce designable internally symmetric monomers with our setup. Overall, this work highlights the capabilities and areas for improvement of zero-shot posterior samplers in motif scaffolding tasks. Code is available at: https://github.com/matsagad/mres-project
A Primer on Variational Inference for Physics-Informed Deep Generative Modelling
Sep 10, 2024
Abstract:Variational inference (VI) is a computationally efficient and scalable methodology for approximate Bayesian inference. It strikes a balance between accuracy of uncertainty quantification and practical tractability. It excels at generative modelling and inversion tasks due to its built-in Bayesian regularisation and flexibility, essential qualities for physics related problems. Deriving the central learning objective for VI must often be tailored to new learning tasks where the nature of the problems dictates the conditional dependence between variables of interest, such as arising in physics problems. In this paper, we provide an accessible and thorough technical introduction to VI for forward and inverse problems, guiding the reader through standard derivations of the VI framework and how it can best be realized through deep learning. We then review and unify recent literature exemplifying the creative flexibility allowed by VI. This paper is designed for a general scientific audience looking to solve physics-based problems with an emphasis on uncertainty quantification.
Kinetic Interacting Particle Langevin Monte Carlo
Jul 08, 2024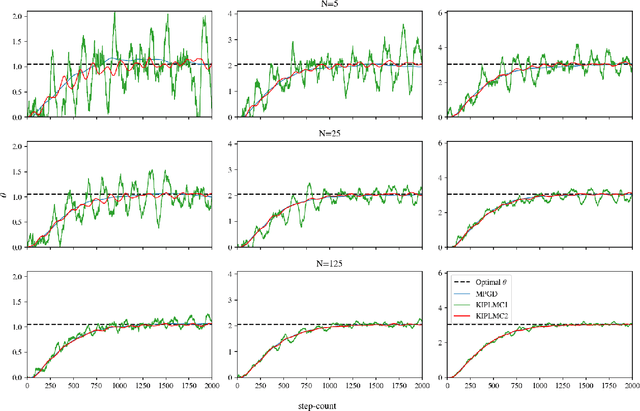

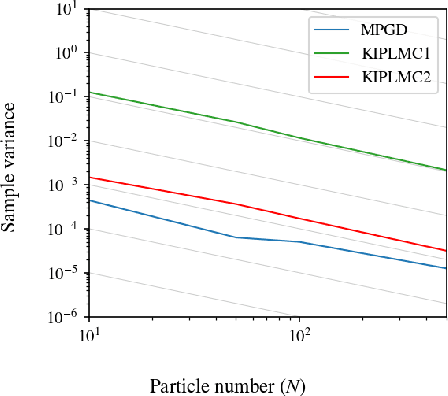
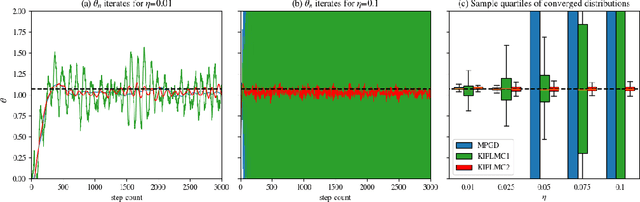
Abstract:This paper introduces and analyses interacting underdamped Langevin algorithms, termed Kinetic Interacting Particle Langevin Monte Carlo (KIPLMC) methods, for statistical inference in latent variable models. We propose a diffusion process that evolves jointly in the space of parameters and latent variables and exploit the fact that the stationary distribution of this diffusion concentrates around the maximum marginal likelihood estimate of the parameters. We then provide two explicit discretisations of this diffusion as practical algorithms to estimate parameters of statistical models. For each algorithm, we obtain nonasymptotic rates of convergence for the case where the joint log-likelihood is strongly concave with respect to latent variables and parameters. In particular, we provide convergence analysis for the diffusion together with the discretisation error, providing convergence rate estimates for the algorithms in Wasserstein-2 distance. To demonstrate the utility of the introduced methodology, we provide numerical experiments that demonstrate the effectiveness of the proposed diffusion for statistical inference and the stability of the numerical integrators utilised for discretisation. Our setting covers a broad number of applications, including unsupervised learning, statistical inference, and inverse problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge