Sampling by averaging: A multiscale approach to score estimation

We introduce a novel framework for efficient sampling from complex, unnormalised target distributions by exploiting multiscale dynamics. Traditional score-based sampling methods either rely on learned approximations of the score function or involve computationally expensive nested Markov chain Monte Carlo (MCMC) loops. In contrast, the proposed approach leverages stochastic averaging within a slow-fast system of stochastic differential equations (SDEs) to estimate intermediate scores along a diffusion path without training or inner-loop MCMC. Two algorithms are developed under this framework: MultALMC, which uses multiscale annealed Langevin dynamics, and MultCDiff, based on multiscale controlled diffusions for the reverse-time Ornstein-Uhlenbeck process. Both overdamped and underdamped variants are considered, with theoretical guarantees of convergence to the desired diffusion path. The framework is extended to handle heavy-tailed target distributions using Student's t-based noise models and tailored fast-process dynamics. Empirical results across synthetic and real-world benchmarks, including multimodal and high-dimensional distributions, demonstrate that the proposed methods are competitive with existing samplers in terms of accuracy and efficiency, without the need for learned models.

Non-asymptotic Analysis of Diffusion Annealed Langevin Monte Carlo for Generative Modelling

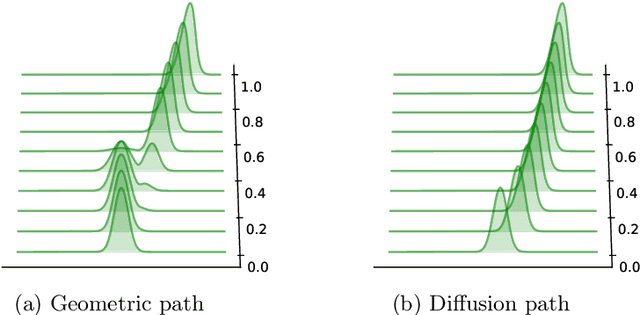
We investigate the theoretical properties of general diffusion (interpolation) paths and their Langevin Monte Carlo implementation, referred to as diffusion annealed Langevin Monte Carlo (DALMC), under weak conditions on the data distribution. Specifically, we analyse and provide non-asymptotic error bounds for the annealed Langevin dynamics where the path of distributions is defined as Gaussian convolutions of the data distribution as in diffusion models. We then extend our results to recently proposed heavy-tailed (Student's t) diffusion paths, demonstrating their theoretical properties for heavy-tailed data distributions for the first time. Our analysis provides theoretical guarantees for a class of score-based generative models that interpolate between a simple distribution (Gaussian or Student's t) and the data distribution in finite time. This approach offers a broader perspective compared to standard score-based diffusion approaches, which are typically based on a forward Ornstein-Uhlenbeck (OU) noising process.

Deep Optimal Sensor Placement for Black Box Stochastic Simulations

Selecting cost-effective optimal sensor configurations for subsequent inference of parameters in black-box stochastic systems faces significant computational barriers. We propose a novel and robust approach, modelling the joint distribution over input parameters and solution with a joint energy-based model, trained on simulation data. Unlike existing simulation-based inference approaches, which must be tied to a specific set of point evaluations, we learn a functional representation of parameters and solution. This is used as a resolution-independent plug-and-play surrogate for the joint distribution, which can be conditioned over any set of points, permitting an efficient approach to sensor placement. We demonstrate the validity of our framework on a variety of stochastic problems, showing that our method provides highly informative sensor locations at a lower computational cost compared to conventional approaches.