Andrew B. Duncan
Sampling by averaging: A multiscale approach to score estimation
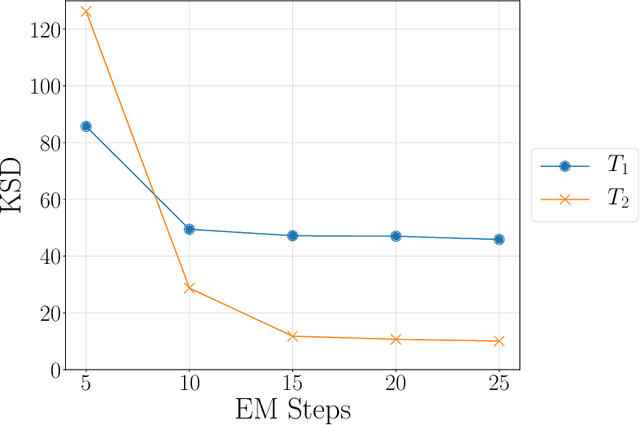
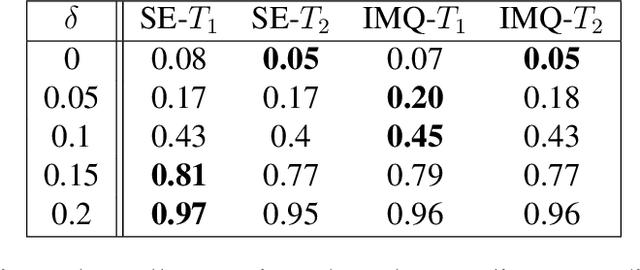
Aug 20, 2025Abstract:We introduce a novel framework for efficient sampling from complex, unnormalised target distributions by exploiting multiscale dynamics. Traditional score-based sampling methods either rely on learned approximations of the score function or involve computationally expensive nested Markov chain Monte Carlo (MCMC) loops. In contrast, the proposed approach leverages stochastic averaging within a slow-fast system of stochastic differential equations (SDEs) to estimate intermediate scores along a diffusion path without training or inner-loop MCMC. Two algorithms are developed under this framework: MultALMC, which uses multiscale annealed Langevin dynamics, and MultCDiff, based on multiscale controlled diffusions for the reverse-time Ornstein-Uhlenbeck process. Both overdamped and underdamped variants are considered, with theoretical guarantees of convergence to the desired diffusion path. The framework is extended to handle heavy-tailed target distributions using Student's t-based noise models and tailored fast-process dynamics. Empirical results across synthetic and real-world benchmarks, including multimodal and high-dimensional distributions, demonstrate that the proposed methods are competitive with existing samplers in terms of accuracy and efficiency, without the need for learned models.
Non-asymptotic Analysis of Diffusion Annealed Langevin Monte Carlo for Generative Modelling
Feb 13, 2025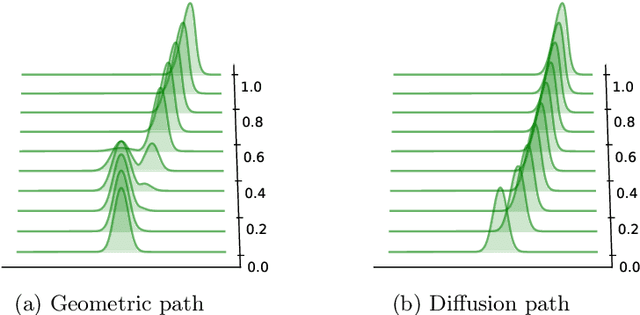
Abstract:We investigate the theoretical properties of general diffusion (interpolation) paths and their Langevin Monte Carlo implementation, referred to as diffusion annealed Langevin Monte Carlo (DALMC), under weak conditions on the data distribution. Specifically, we analyse and provide non-asymptotic error bounds for the annealed Langevin dynamics where the path of distributions is defined as Gaussian convolutions of the data distribution as in diffusion models. We then extend our results to recently proposed heavy-tailed (Student's t) diffusion paths, demonstrating their theoretical properties for heavy-tailed data distributions for the first time. Our analysis provides theoretical guarantees for a class of score-based generative models that interpolate between a simple distribution (Gaussian or Student's t) and the data distribution in finite time. This approach offers a broader perspective compared to standard score-based diffusion approaches, which are typically based on a forward Ornstein-Uhlenbeck (OU) noising process.
Energy-Based Modelling for Discrete and Mixed Data via Heat Equations on Structured Spaces
Dec 02, 2024



Abstract:Energy-based models (EBMs) offer a flexible framework for probabilistic modelling across various data domains. However, training EBMs on data in discrete or mixed state spaces poses significant challenges due to the lack of robust and fast sampling methods. In this work, we propose to train discrete EBMs with Energy Discrepancy, a loss function which only requires the evaluation of the energy function at data points and their perturbed counterparts, thus eliminating the need for Markov chain Monte Carlo. We introduce perturbations of the data distribution by simulating a diffusion process on the discrete state space endowed with a graph structure. This allows us to inform the choice of perturbation from the structure of the modelled discrete variable, while the continuous time parameter enables fine-grained control of the perturbation. Empirically, we demonstrate the efficacy of the proposed approaches in a wide range of applications, including the estimation of discrete densities with non-binary vocabulary and binary image modelling. Finally, we train EBMs on tabular data sets with applications in synthetic data generation and calibrated classification.
Training Discrete Energy-Based Models with Energy Discrepancy
Jul 14, 2023



Abstract:Training energy-based models (EBMs) on discrete spaces is challenging because sampling over such spaces can be difficult. We propose to train discrete EBMs with energy discrepancy (ED), a novel type of contrastive loss functional which only requires the evaluation of the energy function at data points and their perturbed counter parts, thus not relying on sampling strategies like Markov chain Monte Carlo (MCMC). Energy discrepancy offers theoretical guarantees for a broad class of perturbation processes of which we investigate three types: perturbations based on Bernoulli noise, based on deterministic transforms, and based on neighbourhood structures. We demonstrate their relative performance on lattice Ising models, binary synthetic data, and discrete image data sets.
Energy Discrepancies: A Score-Independent Loss for Energy-Based Models
Jul 12, 2023



Abstract:Energy-based models are a simple yet powerful class of probabilistic models, but their widespread adoption has been limited by the computational burden of training them. We propose a novel loss function called Energy Discrepancy (ED) which does not rely on the computation of scores or expensive Markov chain Monte Carlo. We show that ED approaches the explicit score matching and negative log-likelihood loss under different limits, effectively interpolating between both. Consequently, minimum ED estimation overcomes the problem of nearsightedness encountered in score-based estimation methods, while also enjoying theoretical guarantees. Through numerical experiments, we demonstrate that ED learns low-dimensional data distributions faster and more accurately than explicit score matching or contrastive divergence. For high-dimensional image data, we describe how the manifold hypothesis puts limitations on our approach and demonstrate the effectiveness of energy discrepancy by training the energy-based model as a prior of a variational decoder model.
Using Perturbation to Improve Goodness-of-Fit Tests based on Kernelized Stein Discrepancy
Apr 28, 2023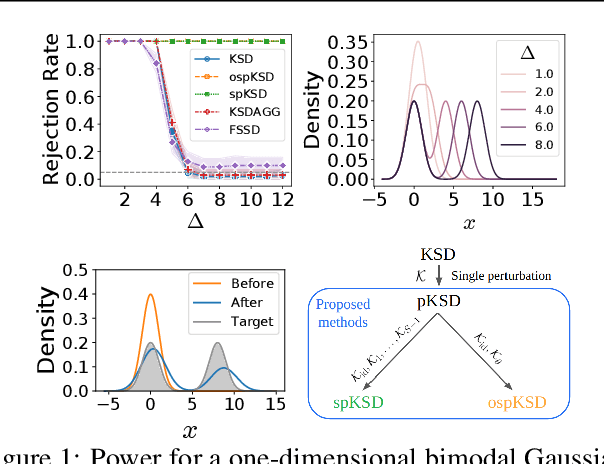
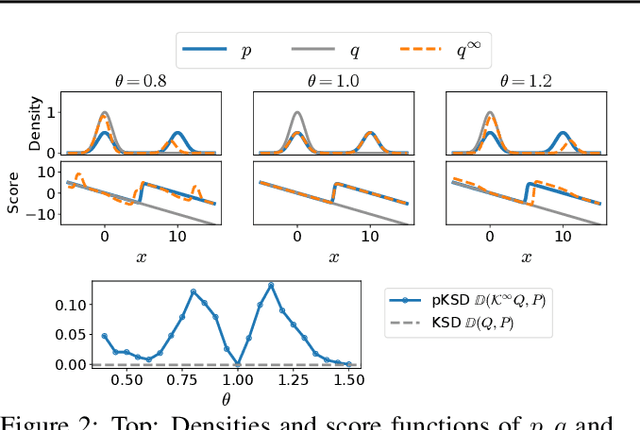
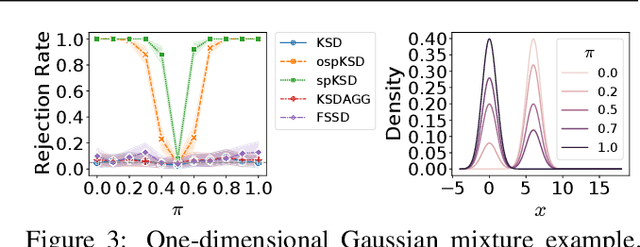
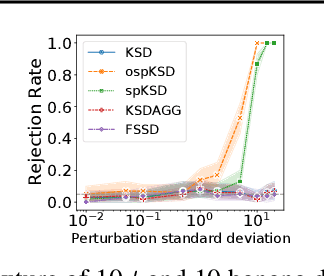
Abstract:Kernelized Stein discrepancy (KSD) is a score-based discrepancy widely used in goodness-of-fit tests. It can be applied even when the target distribution has an unknown normalising factor, such as in Bayesian analysis. We show theoretically and empirically that the KSD test can suffer from low power when the target and the alternative distribution have the same well-separated modes but differ in mixing proportions. We propose to perturb the observed sample via Markov transition kernels, with respect to which the target distribution is invariant. This allows us to then employ the KSD test on the perturbed sample. We provide numerical evidence that with suitably chosen kernels the proposed approach can lead to a substantially higher power than the KSD test.
A High-dimensional Convergence Theorem for U-statistics with Applications to Kernel-based Testing
Feb 24, 2023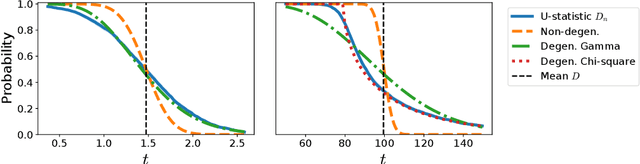
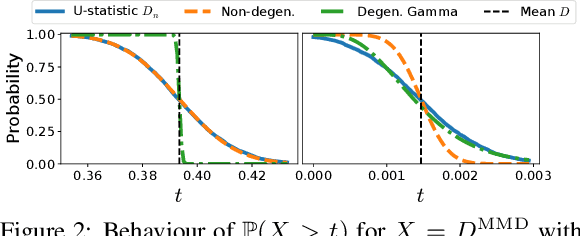
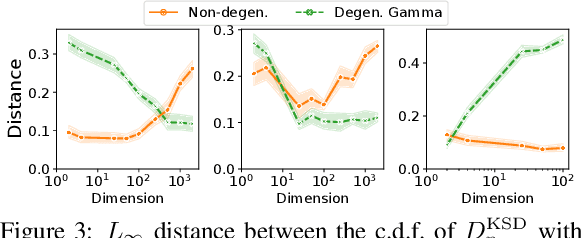

Abstract:We prove a convergence theorem for U-statistics of degree two, where the data dimension $d$ is allowed to scale with sample size $n$. We find that the limiting distribution of a U-statistic undergoes a phase transition from the non-degenerate Gaussian limit to the degenerate limit, regardless of its degeneracy and depending only on a moment ratio. A surprising consequence is that a non-degenerate U-statistic in high dimensions can have a non-Gaussian limit with a larger variance and asymmetric distribution. Our bounds are valid for any finite $n$ and $d$, independent of individual eigenvalues of the underlying function, and dimension-independent under a mild assumption. As an application, we apply our theory to two popular kernel-based distribution tests, MMD and KSD, whose high-dimensional performance has been challenging to study. In a simple empirical setting, our results correctly predict how the test power at a fixed threshold scales with $d$ and the bandwidth.
Batch Bayesian Optimization via Particle Gradient Flows
Sep 10, 2022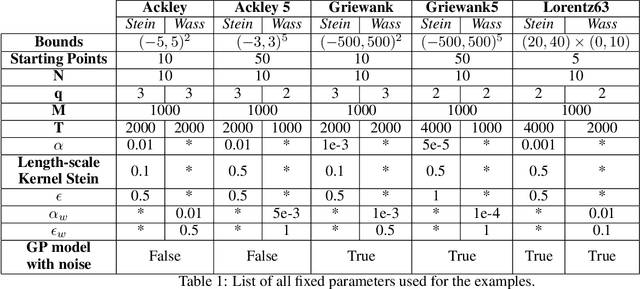
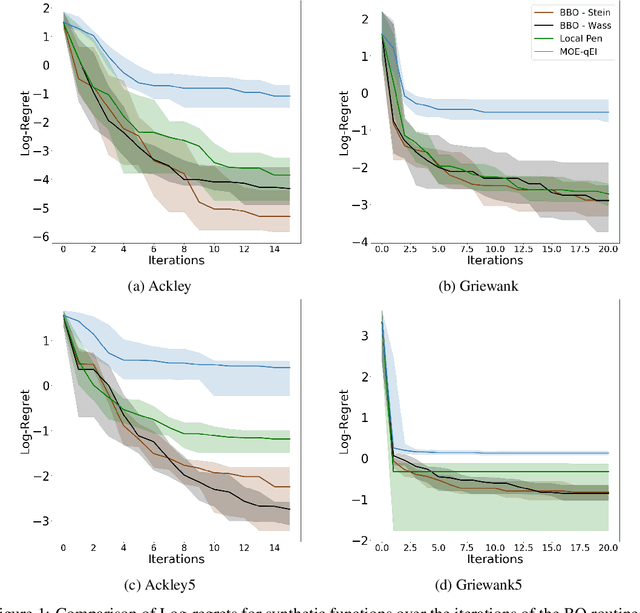
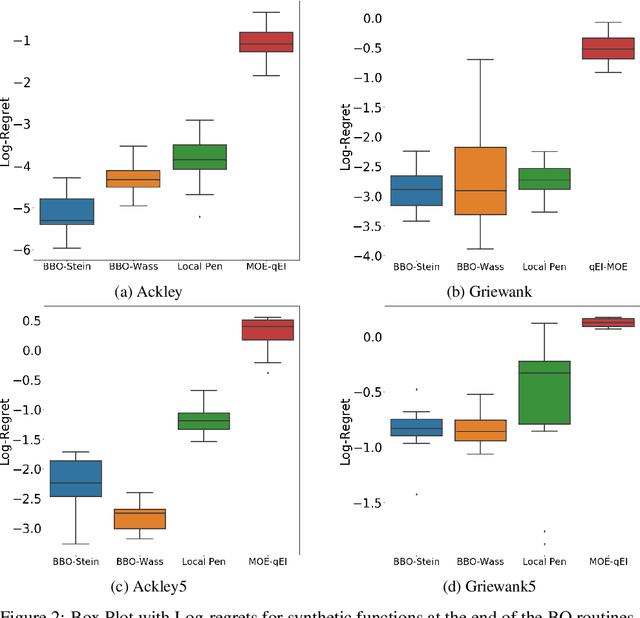
Abstract:Bayesian Optimisation (BO) methods seek to find global optima of objective functions which are only available as a black-box or are expensive to evaluate. Such methods construct a surrogate model for the objective function, quantifying the uncertainty in that surrogate through Bayesian inference. Objective evaluations are sequentially determined by maximising an acquisition function at each step. However, this ancilliary optimisation problem can be highly non-trivial to solve, due to the non-convexity of the acquisition function, particularly in the case of batch Bayesian optimisation, where multiple points are selected in every step. In this work we reformulate batch BO as an optimisation problem over the space of probability measures. We construct a new acquisition function based on multipoint expected improvement which is convex over the space of probability measures. Practical schemes for solving this `inner' optimisation problem arise naturally as gradient flows of this objective function. We demonstrate the efficacy of this new method on different benchmark functions and compare with state-of-the-art batch BO methods.
A Spectral Representation of Kernel Stein Discrepancy with Application to Goodness-of-Fit Tests for Measures on Infinite Dimensional Hilbert Spaces
Jun 09, 2022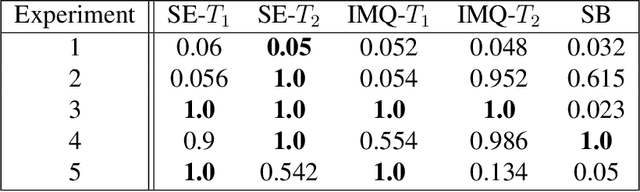

Abstract:Kernel Stein discrepancy (KSD) is a widely used kernel-based non-parametric measure of discrepancy between probability measures. It is often employed in the scenario where a user has a collection of samples from a candidate probability measure and wishes to compare them against a specified target probability measure. A useful property of KSD is that it may be calculated with samples from only the candidate measure and without knowledge of the normalising constant of the target measure. KSD has been employed in a range of settings including goodness-of-fit testing, parametric inference, MCMC output assessment and generative modelling. Two main issues with current KSD methodology are (i) the lack of applicability beyond the finite dimensional Euclidean setting and (ii) a lack of clarity on what influences KSD performance. This paper provides a novel spectral representation of KSD which remedies both of these, making KSD applicable to Hilbert-valued data and revealing the impact of kernel and Stein operator choice on the KSD. We demonstrate the efficacy of the proposed methodology by performing goodness-of-fit tests for various Gaussian and non-Gaussian functional models in a number of synthetic data experiments.
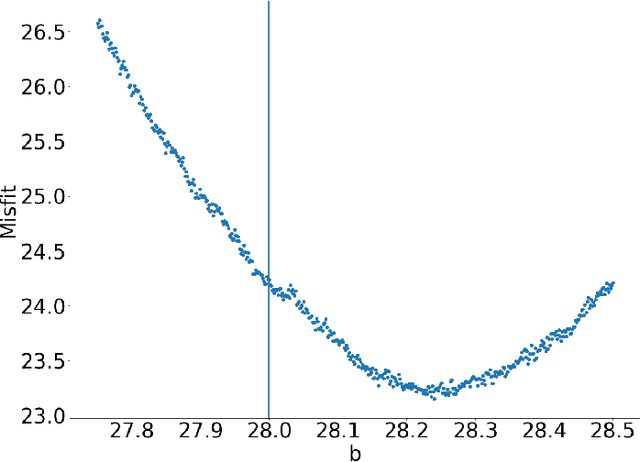
Ensemble Inference Methods for Models With Noisy and Expensive Likelihoods
Apr 07, 2021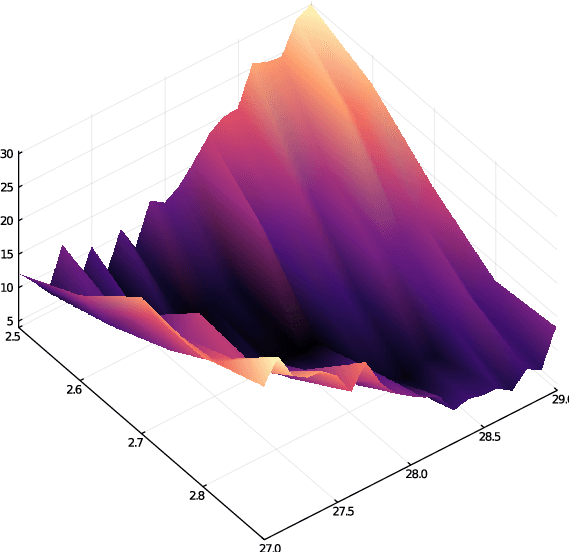
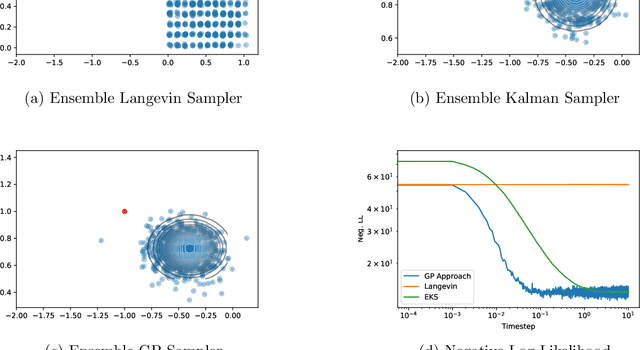
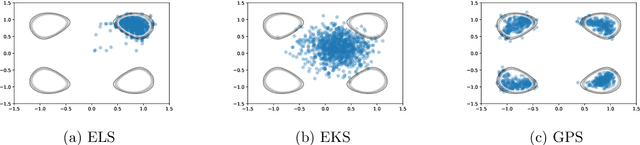
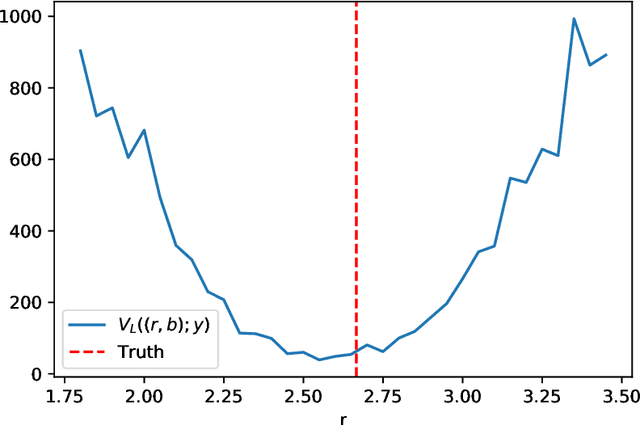
Abstract:The increasing availability of data presents an opportunity to calibrate unknown parameters which appear in complex models of phenomena in the biomedical, physical and social sciences. However, model complexity often leads to parameter-to-data maps which are expensive to evaluate and are only available through noisy approximations. This paper is concerned with the use of interacting particle systems for the solution of the resulting inverse problems for parameters. Of particular interest is the case where the available forward model evaluations are subject to rapid fluctuations, in parameter space, superimposed on the smoothly varying large scale parametric structure of interest. Multiscale analysis is used to study the behaviour of interacting particle system algorithms when such rapid fluctuations, which we refer to as noise, pollute the large scale parametric dependence of the parameter-to-data map. Ensemble Kalman methods (which are derivative-free) and Langevin-based methods (which use the derivative of the parameter-to-data map) are compared in this light. The ensemble Kalman methods are shown to behave favourably in the presence of noise in the parameter-to-data map, whereas Langevin methods are adversely affected. On the other hand, Langevin methods have the correct equilibrium distribution in the setting of noise-free forward models, whilst ensemble Kalman methods only provide an uncontrolled approximation, except in the linear case. Therefore a new class of algorithms, ensemble Gaussian process samplers, which combine the benefits of both ensemble Kalman and Langevin methods, are introduced and shown to perform favourably.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge