Particle Semi-Implicit Variational Inference

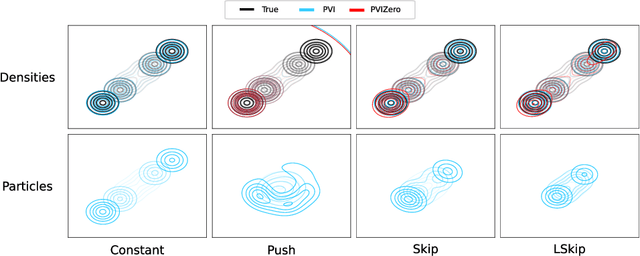
Semi-implicit variational inference (SIVI) enriches the expressiveness of variational families by utilizing a kernel and a mixing distribution to hierarchically define the variational distribution. Existing SIVI methods parameterize the mixing distribution using implicit distributions, leading to intractable variational densities. As a result, directly maximizing the evidence lower bound (ELBO) is not possible and so, they resort to either: optimizing bounds on the ELBO, employing costly inner-loop Markov chain Monte Carlo runs, or solving minimax objectives. In this paper, we propose a novel method for SIVI called Particle Variational Inference (PVI) which employs empirical measures to approximate the optimal mixing distributions characterized as the minimizer of a natural free energy functional via a particle approximation of an Euclidean--Wasserstein gradient flow. This approach means that, unlike prior works, PVI can directly optimize the ELBO; furthermore, it makes no parametric assumption about the mixing distribution. Our empirical results demonstrate that PVI performs favourably against other SIVI methods across various tasks. Moreover, we provide a theoretical analysis of the behaviour of the gradient flow of a related free energy functional: establishing the existence and uniqueness of solutions as well as propagation of chaos results.

Momentum Particle Maximum Likelihood

Maximum likelihood estimation (MLE) of latent variable models is often recast as an optimization problem over the extended space of parameters and probability distributions. For example, the Expectation Maximization (EM) algorithm can be interpreted as coordinate descent applied to a suitable free energy functional over this space. Recently, this perspective has been combined with insights from optimal transport and Wasserstein gradient flows to develop particle-based algorithms applicable to wider classes of models than standard EM. Drawing inspiration from prior works which interpret `momentum-enriched' optimisation algorithms as discretizations of ordinary differential equations, we propose an analogous dynamical systems-inspired approach to minimizing the free energy functional over the extended space of parameters and probability distributions. The result is a dynamic system that blends elements of Nesterov's Accelerated Gradient method, the underdamped Langevin diffusion, and particle methods. Under suitable assumptions, we establish quantitative convergence of the proposed system to the unique minimiser of the functional in continuous time. We then propose a numerical discretization of this system which enables its application to parameter estimation in latent variable models. Through numerical experiments, we demonstrate that the resulting algorithm converges faster than existing methods and compares favourably with other (approximate) MLE algorithms.

Energy Discrepancies: A Score-Independent Loss for Energy-Based Models

Energy-based models are a simple yet powerful class of probabilistic models, but their widespread adoption has been limited by the computational burden of training them. We propose a novel loss function called Energy Discrepancy (ED) which does not rely on the computation of scores or expensive Markov chain Monte Carlo. We show that ED approaches the explicit score matching and negative log-likelihood loss under different limits, effectively interpolating between both. Consequently, minimum ED estimation overcomes the problem of nearsightedness encountered in score-based estimation methods, while also enjoying theoretical guarantees. Through numerical experiments, we demonstrate that ED learns low-dimensional data distributions faster and more accurately than explicit score matching or contrastive divergence. For high-dimensional image data, we describe how the manifold hypothesis puts limitations on our approach and demonstrate the effectiveness of energy discrepancy by training the energy-based model as a prior of a variational decoder model.

Faking feature importance: A cautionary tale on the use of differentially-private synthetic data

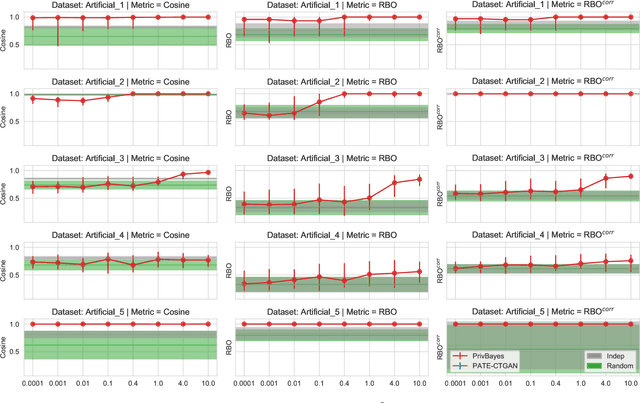
Synthetic datasets are often presented as a silver-bullet solution to the problem of privacy-preserving data publishing. However, for many applications, synthetic data has been shown to have limited utility when used to train predictive models. One promising potential application of these data is in the exploratory phase of the machine learning workflow, which involves understanding, engineering and selecting features. This phase often involves considerable time, and depends on the availability of data. There would be substantial value in synthetic data that permitted these steps to be carried out while, for example, data access was being negotiated, or with fewer information governance restrictions. This paper presents an empirical analysis of the agreement between the feature importance obtained from raw and from synthetic data, on a range of artificially generated and real-world datasets (where feature importance represents how useful each feature is when predicting a the outcome). We employ two differentially-private methods to produce synthetic data, and apply various utility measures to quantify the agreement in feature importance as this varies with the level of privacy. Our results indicate that synthetic data can sometimes preserve several representations of the ranking of feature importance in simple settings but their performance is not consistent and depends upon a number of factors. Particular caution should be exercised in more nuanced real-world settings, where synthetic data can lead to differences in ranked feature importance that could alter key modelling decisions. This work has important implications for developing synthetic versions of highly sensitive data sets in fields such as finance and healthcare.

$\mathcal{F}$-EBM: Energy Based Learning of Functional Data

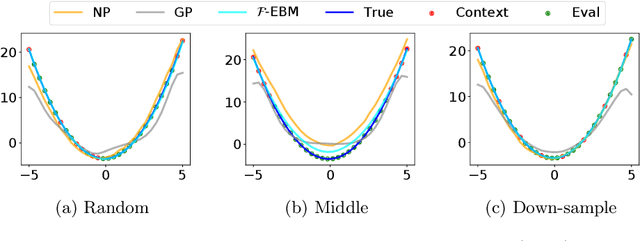
Energy-Based Models (EBMs) have proven to be a highly effective approach for modelling densities on finite-dimensional spaces. Their ability to incorporate domain-specific choices and constraints into the structure of the model through composition make EBMs an appealing candidate for applications in physics, biology and computer vision and various other fields. In this work, we present a novel class of EBM which is able to learn distributions of functions (such as curves or surfaces) from functional samples evaluated at finitely many points. Two unique challenges arise in the functional context. Firstly, training data is often not evaluated along a fixed set of points. Secondly, steps must be taken to control the behaviour of the model between evaluation points, to mitigate overfitting. The proposed infinite-dimensional EBM employs a latent Gaussian process, which is weighted spectrally by an energy function parameterised with a neural network. The resulting EBM has the ability to utilize irregularly sampled training data and can output predictions at any resolution, providing an effective approach to up-scaling functional data. We demonstrate the efficacy of our proposed approach for modelling a range of datasets, including data collected from Standard and Poor's 500 (S\&P) and UK National grid.

Kernel Stein Tests for Multiple Model Comparison

We address the problem of non-parametric multiple model comparison: given $l$ candidate models, decide whether each candidate is as good as the best one(s) or worse than it. We propose two statistical tests, each controlling a different notion of decision errors. The first test, building on the post selection inference framework, provably controls the number of best models that are wrongly declared worse (false positive rate). The second test is based on multiple correction, and controls the proportion of the models declared worse but are in fact as good as the best (false discovery rate). We prove that under appropriate conditions the first test can yield a higher true positive rate than the second. Experimental results on toy and real (CelebA, Chicago Crime data) problems show that the two tests have high true positive rates with well-controlled error rates. By contrast, the naive approach of choosing the model with the lowest score without correction leads to more false positives.

More Powerful Selective Kernel Tests for Feature Selection

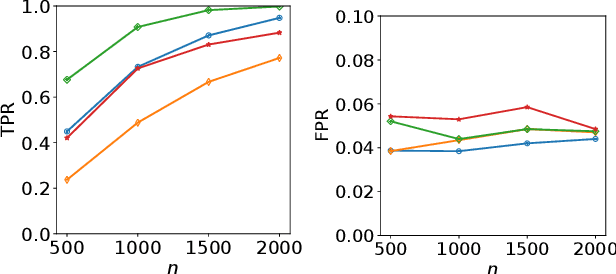
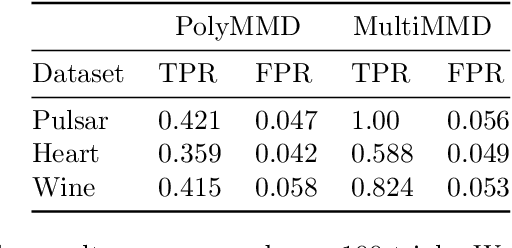
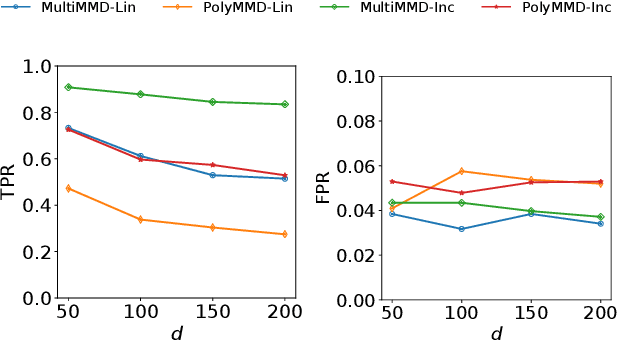
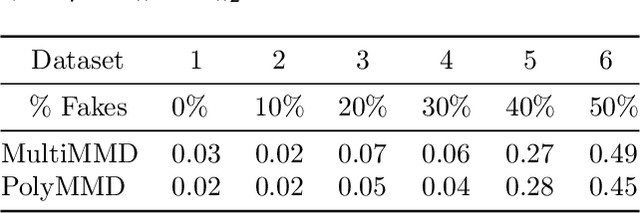
Refining one's hypotheses in the light of data is a commonplace scientific practice, however, this approach introduces selection bias and can lead to specious statistical analysis. One approach of addressing this phenomena is via conditioning on the selection procedure, i.e., how we have used the data to generate our hypotheses, and prevents information to be used again after selection. Many selective inference (a.k.a. post-selection inference) algorithms typically take this approach but will "over-condition" for sake of tractability. While this practice obtains well calibrated $p$-values, it can incur a major loss in power. In our work, we extend two recent proposals for selecting features using the Maximum Mean Discrepancy and Hilbert Schmidt Independence Criterion to condition on the minimal conditioning event. We show how recent advances in multiscale bootstrap makes conditioning on the minimal selection event possible and demonstrate our proposal over a range of synthetic and real world experiments. Our results show that our proposed test is indeed more powerful in most scenarios.