$\mathcal{F}$-EBM: Energy Based Learning of Functional Data
Paper and Code
Feb 04, 2022


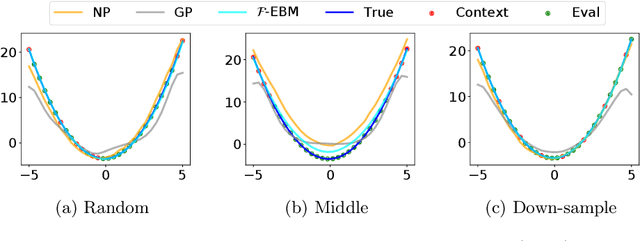
Energy-Based Models (EBMs) have proven to be a highly effective approach for modelling densities on finite-dimensional spaces. Their ability to incorporate domain-specific choices and constraints into the structure of the model through composition make EBMs an appealing candidate for applications in physics, biology and computer vision and various other fields. In this work, we present a novel class of EBM which is able to learn distributions of functions (such as curves or surfaces) from functional samples evaluated at finitely many points. Two unique challenges arise in the functional context. Firstly, training data is often not evaluated along a fixed set of points. Secondly, steps must be taken to control the behaviour of the model between evaluation points, to mitigate overfitting. The proposed infinite-dimensional EBM employs a latent Gaussian process, which is weighted spectrally by an energy function parameterised with a neural network. The resulting EBM has the ability to utilize irregularly sampled training data and can output predictions at any resolution, providing an effective approach to up-scaling functional data. We demonstrate the efficacy of our proposed approach for modelling a range of datasets, including data collected from Standard and Poor's 500 (S\&P) and UK National grid.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge