Error bounds for particle gradient descent, and extensions of the log-Sobolev and Talagrand inequalities

We prove non-asymptotic error bounds for particle gradient descent (PGD)~(Kuntz et al., 2023), a recently introduced algorithm for maximum likelihood estimation of large latent variable models obtained by discretizing a gradient flow of the free energy. We begin by showing that, for models satisfying a condition generalizing both the log-Sobolev and the Polyak--{\L}ojasiewicz inequalities (LSI and P{\L}I, respectively), the flow converges exponentially fast to the set of minimizers of the free energy. We achieve this by extending a result well-known in the optimal transport literature (that the LSI implies the Talagrand inequality) and its counterpart in the optimization literature (that the P{\L}I implies the so-called quadratic growth condition), and applying it to our new setting. We also generalize the Bakry--\'Emery Theorem and show that the LSI/P{\L}I generalization holds for models with strongly concave log-likelihoods. For such models, we further control PGD's discretization error, obtaining non-asymptotic error bounds. While we are motivated by the study of PGD, we believe that the inequalities and results we extend may be of independent interest.

Momentum Particle Maximum Likelihood

Maximum likelihood estimation (MLE) of latent variable models is often recast as an optimization problem over the extended space of parameters and probability distributions. For example, the Expectation Maximization (EM) algorithm can be interpreted as coordinate descent applied to a suitable free energy functional over this space. Recently, this perspective has been combined with insights from optimal transport and Wasserstein gradient flows to develop particle-based algorithms applicable to wider classes of models than standard EM. Drawing inspiration from prior works which interpret `momentum-enriched' optimisation algorithms as discretizations of ordinary differential equations, we propose an analogous dynamical systems-inspired approach to minimizing the free energy functional over the extended space of parameters and probability distributions. The result is a dynamic system that blends elements of Nesterov's Accelerated Gradient method, the underdamped Langevin diffusion, and particle methods. Under suitable assumptions, we establish quantitative convergence of the proposed system to the unique minimiser of the functional in continuous time. We then propose a numerical discretization of this system which enables its application to parameter estimation in latent variable models. Through numerical experiments, we demonstrate that the resulting algorithm converges faster than existing methods and compares favourably with other (approximate) MLE algorithms.

Scalable particle-based alternatives to EM

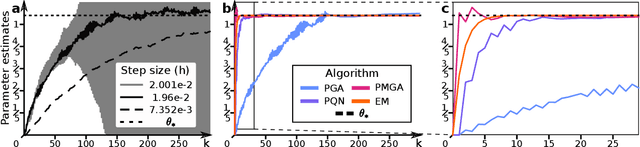
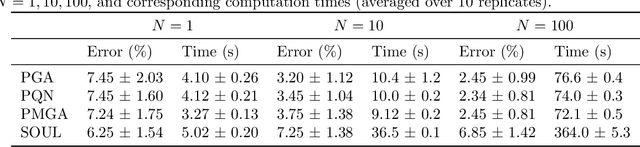
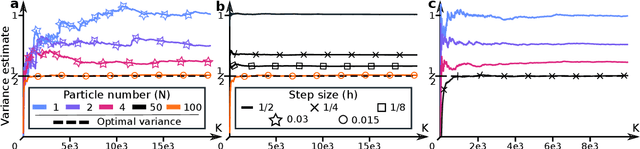
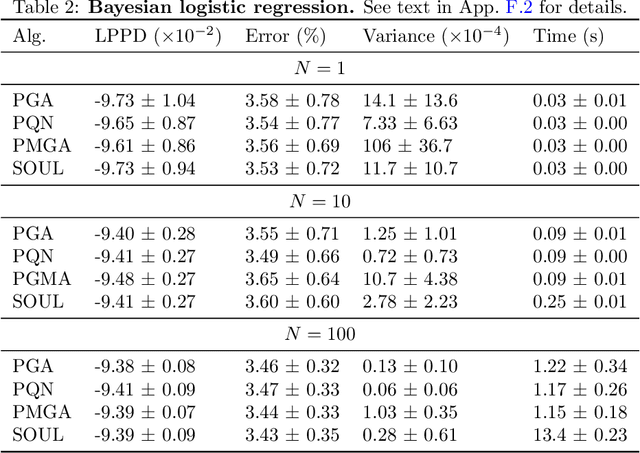
Building on (Neal and Hinton, 1998), where the problem tackled by EM is recast as the optimization of a free energy functional on an infinite-dimensional space, we obtain three practical particle-based alternatives to EM applicable to broad classes of models. All three are derived through straightforward discretizations of gradient flows associated with the functional. The novel algorithms scale well to high-dimensional settings and outperform existing state-of-the-art methods in numerical experiments.