Dose-finding design based on level set estimation in phase I cancer clinical trials

The primary objective of phase I cancer clinical trials is to evaluate the safety of a new experimental treatment and to find the maximum tolerated dose (MTD). We show that the MTD estimation problem can be regarded as a level set estimation (LSE) problem whose objective is to determine the regions where an unknown function value is above or below a given threshold. Then, we propose a novel dose-finding design in the framework of LSE. The proposed design determines the next dose on the basis of an acquisition function incorporating uncertainty in the posterior distribution of the dose-toxicity curve as well as overdose control. Simulation experiments show that the proposed LSE design achieves a higher accuracy in estimating the MTD and involves a lower risk of overdosing allocation compared to existing designs, thereby indicating that it provides an effective methodology for phase I cancer clinical trial design.

More Powerful Selective Kernel Tests for Feature Selection

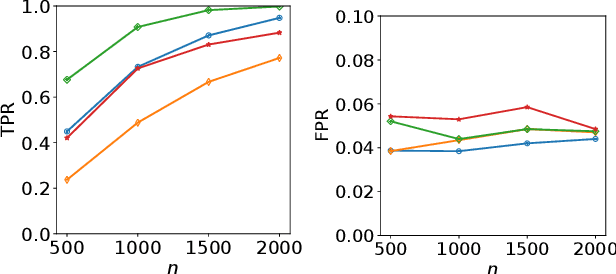
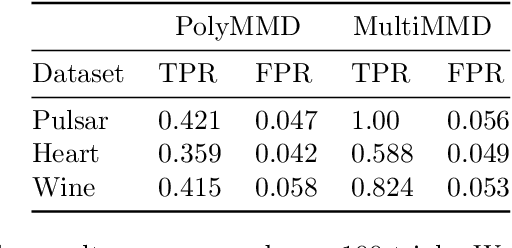
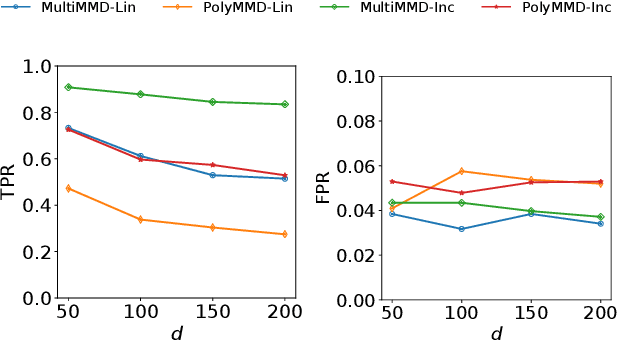
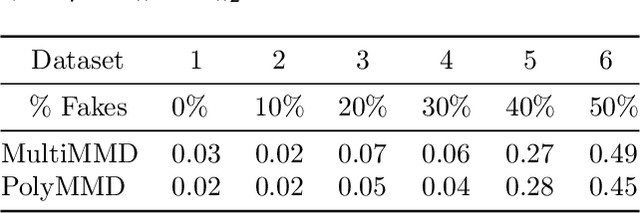
Refining one's hypotheses in the light of data is a commonplace scientific practice, however, this approach introduces selection bias and can lead to specious statistical analysis. One approach of addressing this phenomena is via conditioning on the selection procedure, i.e., how we have used the data to generate our hypotheses, and prevents information to be used again after selection. Many selective inference (a.k.a. post-selection inference) algorithms typically take this approach but will "over-condition" for sake of tractability. While this practice obtains well calibrated $p$-values, it can incur a major loss in power. In our work, we extend two recent proposals for selecting features using the Maximum Mean Discrepancy and Hilbert Schmidt Independence Criterion to condition on the minimal conditioning event. We show how recent advances in multiscale bootstrap makes conditioning on the minimal selection event possible and demonstrate our proposal over a range of synthetic and real world experiments. Our results show that our proposed test is indeed more powerful in most scenarios.