Likelihood Variance as Text Importance for Resampling Texts to Map Language Models

We address the computational cost of constructing a model map, which embeds diverse language models into a common space for comparison via KL divergence. The map relies on log-likelihoods over a large text set, making the cost proportional to the number of texts. To reduce this cost, we propose a resampling method that selects important texts with weights proportional to the variance of log-likelihoods across models for each text. Our method significantly reduces the number of required texts while preserving the accuracy of KL divergence estimates. Experiments show that it achieves comparable performance to uniform sampling with about half as many texts, and also facilitates efficient incorporation of new models into an existing map. These results enable scalable and efficient construction of language model maps.

Revealing Language Model Trajectories via Kullback-Leibler Divergence

A recently proposed method enables efficient estimation of the KL divergence between language models, including models with different architectures, by assigning coordinates based on log-likelihood vectors. To better understand the behavior of this metric, we systematically evaluate KL divergence across a wide range of conditions using publicly available language models. Our analysis covers comparisons between pretraining checkpoints, fine-tuned and base models, and layers via the logit lens. We find that trajectories of language models, as measured by KL divergence, exhibit a spiral structure during pretraining and thread-like progressions across layers. Furthermore, we show that, in terms of diffusion exponents, model trajectories in the log-likelihood space are more constrained than those in weight space.

Beyond Chains: Bridging Large Language Models and Knowledge Bases in Complex Question Answering

Knowledge Base Question Answering (KBQA) aims to answer natural language questions using structured knowledge from KBs. While LLM-only approaches offer generalization, they suffer from outdated knowledge, hallucinations, and lack of transparency. Chain-based KG-RAG methods address these issues by incorporating external KBs, but are limited to simple chain-structured questions due to the absence of planning and logical structuring. Inspired by semantic parsing methods, we propose PDRR: a four-stage framework consisting of Predict, Decompose, Retrieve, and Reason. Our method first predicts the question type and decomposes the question into structured triples. Then retrieves relevant information from KBs and guides the LLM as an agent to reason over and complete the decomposed triples. Experimental results demonstrate that PDRR consistently outperforms existing methods across various LLM backbones and achieves superior performance on both chain-structured and non-chain complex questions.

Visuospatial Cognitive Assistant

Video-based spatial cognition is vital for robotics and embodied AI but challenges current Vision-Language Models (VLMs). This paper makes two key contributions. First, we introduce ViCA (Visuospatial Cognitive Assistant)-322K, a diverse dataset of 322,003 QA pairs from real-world indoor videos (ARKitScenes, ScanNet, ScanNet++), offering supervision for 3D metadata-grounded queries and video-based complex reasoning. Second, we develop ViCA-7B, fine-tuned on ViCA-322K, which achieves new state-of-the-art on all eight VSI-Bench tasks, outperforming existing models, including larger ones (e.g., +26.1 on Absolute Distance). For interpretability, we present ViCA-Thinking-2.68K, a dataset with explicit reasoning chains, and fine-tune ViCA-7B to create ViCA-7B-Thinking, a model that articulates its spatial reasoning. Our work highlights the importance of targeted data and suggests paths for improved temporal-spatial modeling. We release all resources to foster research in robust visuospatial intelligence.

Towards Visuospatial Cognition via Hierarchical Fusion of Visual Experts

While Multimodal Large Language Models (MLLMs) excel at general vision-language tasks, visuospatial cognition - reasoning about spatial layouts, relations, and dynamics - remains a significant challenge. Existing models often lack the necessary architectural components and specialized training data for fine-grained spatial understanding. We introduce ViCA2 (Visuospatial Cognitive Assistant 2), a novel MLLM designed to enhance spatial reasoning. ViCA2 features a dual vision encoder architecture integrating SigLIP for semantics and Hiera for spatial structure, coupled with a token ratio control mechanism for efficiency. We also developed ViCA-322K, a new large-scale dataset with over 322,000 spatially grounded question-answer pairs for targeted instruction tuning. On the challenging VSI-Bench benchmark, our ViCA2-7B model achieves a state-of-the-art average score of 56.8, significantly surpassing larger open-source models (e.g., LLaVA-NeXT-Video-72B, 40.9) and leading proprietary models (Gemini-1.5 Pro, 45.4). This demonstrates the effectiveness of our approach in achieving strong visuospatial intelligence with a compact model. We release ViCA2, its codebase, and the ViCA-322K dataset to facilitate further research.

DeLTa: A Decoding Strategy based on Logit Trajectory Prediction Improves Factuality and Reasoning Ability

Large Language Models (LLMs) are increasingly being used in real-world applications. However, concerns about the reliability of the content they generate persist, as it frequently deviates from factual correctness or exhibits deficiencies in logical reasoning. This paper proposes a novel decoding strategy aimed at enhancing both factual accuracy and inferential reasoning without requiring any modifications to the architecture or pre-trained parameters of LLMs. Our approach adjusts next-token probabilities by analyzing the trajectory of logits from lower to higher layers in Transformers and applying linear regression. We find that this Decoding by Logit Trajectory-based approach (DeLTa) effectively reinforces factuality and reasoning while mitigating incorrect generation. Experiments on TruthfulQA demonstrate that DeLTa attains up to a 4.9% improvement over the baseline. Furthermore, it enhances performance by up to 8.1% on StrategyQA and 7.3% on GSM8K, both of which demand strong reasoning capabilities.

Mapping 1,000+ Language Models via the Log-Likelihood Vector

To compare autoregressive language models at scale, we propose using log-likelihood vectors computed on a predefined text set as model features. This approach has a solid theoretical basis: when treated as model coordinates, their squared Euclidean distance approximates the Kullback-Leibler divergence of text-generation probabilities. Our method is highly scalable, with computational cost growing linearly in both the number of models and text samples, and is easy to implement as the required features are derived from cross-entropy loss. Applying this method to over 1,000 language models, we constructed a "model map," providing a new perspective on large-scale model analysis.

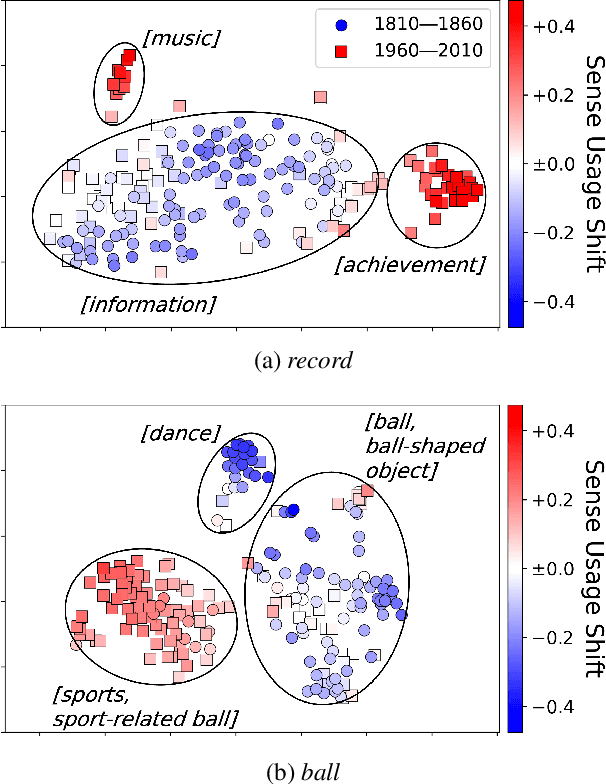
Quantifying Lexical Semantic Shift via Unbalanced Optimal Transport

Lexical semantic change detection aims to identify shifts in word meanings over time. While existing methods using embeddings from a diachronic corpus pair estimate the degree of change for target words, they offer limited insight into changes at the level of individual usage instances. To address this, we apply Unbalanced Optimal Transport (UOT) to sets of contextualized word embeddings, capturing semantic change through the excess and deficit in the alignment between usage instances. In particular, we propose Sense Usage Shift (SUS), a measure that quantifies changes in the usage frequency of a word sense at each usage instance. By leveraging SUS, we demonstrate that several challenges in semantic change detection can be addressed in a unified manner, including quantifying instance-level semantic change and word-level tasks such as measuring the magnitude of semantic change and the broadening or narrowing of meaning.

Zipfian Whitening

The word embedding space in neural models is skewed, and correcting this can improve task performance. We point out that most approaches for modeling, correcting, and measuring the symmetry of an embedding space implicitly assume that the word frequencies are uniform; in reality, word frequencies follow a highly non-uniform distribution, known as Zipf's law. Surprisingly, simply performing PCA whitening weighted by the empirical word frequency that follows Zipf's law significantly improves task performance, surpassing established baselines. From a theoretical perspective, both our approach and existing methods can be clearly categorized: word representations are distributed according to an exponential family with either uniform or Zipfian base measures. By adopting the latter approach, we can naturally emphasize informative low-frequency words in terms of their vector norm, which becomes evident from the information-geometric perspective, and in terms of the loss functions for imbalanced classification. Additionally, our theory corroborates that popular natural language processing methods, such as skip-gram negative sampling, WhiteningBERT, and headless language models, work well just because their word embeddings encode the empirical word frequency into the underlying probabilistic model.

Understanding Higher-Order Correlations Among Semantic Components in Embeddings

Independent Component Analysis (ICA) is an effective method for interpreting the intrinsic geometric structure of embeddings as semantic components. While ICA theory assumes that embeddings can be linearly decomposed into independent components, real-world data often do not satisfy this assumption. Consequently, there are remaining non-independencies between the estimated components that ICA cannot eliminate. We quantified these non-independencies using higher-order correlations and demonstrated that when the higher-order correlation between two components is large, it indicates a strong semantic association between them. The entire structure was revealed through visualization using a maximum spanning tree of semantic components. These findings allow for further understanding of embeddings through ICA.