Nonparametric logistic regression with deep learning

Consider the nonparametric logistic regression problem. In the logistic regression, we usually consider the maximum likelihood estimator, and the excess risk is the expectation of the Kullback-Leibler (KL) divergence between the true and estimated conditional class probabilities. However, in the nonparametric logistic regression, the KL divergence could diverge easily, and thus, the convergence of the excess risk is difficult to prove or does not hold. Several existing studies show the convergence of the KL divergence under strong assumptions. In most cases, our goal is to estimate the true conditional class probabilities. Thus, instead of analyzing the excess risk itself, it suffices to show the consistency of the maximum likelihood estimator in some suitable metric. In this paper, using a simple unified approach for analyzing the nonparametric maximum likelihood estimator (NPMLE), we directly derive the convergence rates of the NPMLE in the Hellinger distance under mild assumptions. Although our results are similar to the results in some existing studies, we provide simple and more direct proofs for these results. As an important application, we derive the convergence rates of the NPMLE with deep neural networks and show that the derived rate nearly achieves the minimax optimal rate.

Convex Clustering through MM: An Efficient Algorithm to Perform Hierarchical Clustering

Convex clustering is a modern method with both hierarchical and $k$-means clustering characteristics. Although convex clustering can capture the complex clustering structure hidden in data, the existing convex clustering algorithms are not scalable to large data sets with sample sizes greater than ten thousand. Moreover, it is known that convex clustering sometimes fails to produce hierarchical clustering structures. This undesirable phenomenon is called cluster split and makes it difficult to interpret clustering results. In this paper, we propose convex clustering through majorization-minimization (CCMM) -- an iterative algorithm that uses cluster fusions and sparsity to enforce a complete cluster hierarchy with reduced memory usage. In the CCMM algorithm, the diagonal majorization technique makes a highly efficient update for each iteration. With a current desktop computer, the CCMM algorithm can solve a single clustering problem featuring over one million objects in seven-dimensional space within 70 seconds.

More Powerful Selective Kernel Tests for Feature Selection

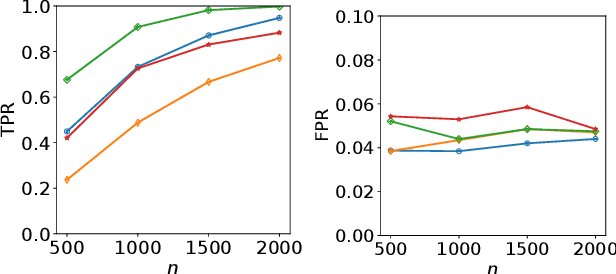
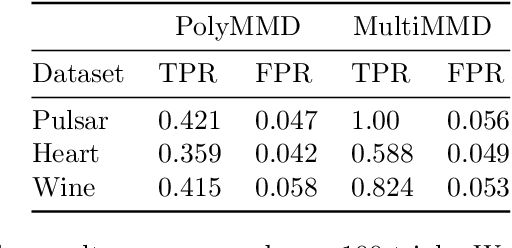
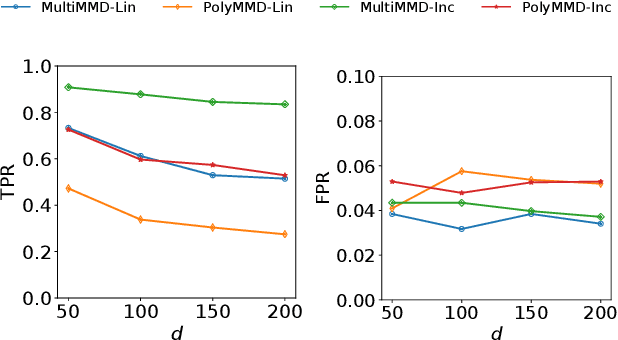
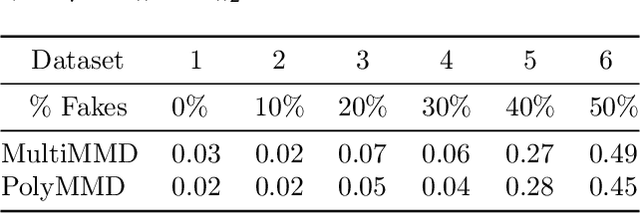
Refining one's hypotheses in the light of data is a commonplace scientific practice, however, this approach introduces selection bias and can lead to specious statistical analysis. One approach of addressing this phenomena is via conditioning on the selection procedure, i.e., how we have used the data to generate our hypotheses, and prevents information to be used again after selection. Many selective inference (a.k.a. post-selection inference) algorithms typically take this approach but will "over-condition" for sake of tractability. While this practice obtains well calibrated $p$-values, it can incur a major loss in power. In our work, we extend two recent proposals for selecting features using the Maximum Mean Discrepancy and Hilbert Schmidt Independence Criterion to condition on the minimal conditioning event. We show how recent advances in multiscale bootstrap makes conditioning on the minimal selection event possible and demonstrate our proposal over a range of synthetic and real world experiments. Our results show that our proposed test is indeed more powerful in most scenarios.

Fast generalization error bound of deep learning without scale invariance of activation functions

In theoretical analysis of deep learning, discovering which features of deep learning lead to good performance is an important task. In this paper, using the framework for analyzing the generalization error developed in Suzuki (2018), we derive a fast learning rate for deep neural networks with more general activation functions. In Suzuki (2018), assuming the scale invariance of activation functions, the tight generalization error bound of deep learning was derived. They mention that the scale invariance of the activation function is essential to derive tight error bounds. Whereas the rectified linear unit (ReLU; Nair and Hinton, 2010) satisfies the scale invariance, the other famous activation functions including the sigmoid and the hyperbolic tangent functions, and the exponential linear unit (ELU; Clevert et al., 2016) does not satisfy this condition. The existing analysis indicates a possibility that a deep learning with the non scale invariant activations may have a slower convergence rate of $O(1/\sqrt{n})$ when one with the scale invariant activations can reach a rate faster than $O(1/\sqrt{n})$. In this paper, without the scale invariance of activation functions, we derive the tight generalization error bound which is essentially the same as that of Suzuki (2018). From this result, at least in the framework of Suzuki (2018), it is shown that the scale invariance of the activation functions is not essential to get the fast rate of convergence. Simultaneously, it is also shown that the theoretical framework proposed by Suzuki (2018) can be widely applied for analysis of deep learning with general activation functions.

Strong Consistency of Reduced K-means Clustering

Reduced k-means clustering is a method for clustering objects in a low-dimensional subspace. The advantage of this method is that both clustering of objects and low-dimensional subspace reflecting the cluster structure are simultaneously obtained. In this paper, the relationship between conventional k-means clustering and reduced k-means clustering is discussed. Conditions ensuring almost sure convergence of the estimator of reduced k-means clustering as unboundedly increasing sample size have been presented. The results for a more general model considering conventional k-means clustering and reduced k-means clustering are provided in this paper. Moreover, a new criterion and its consistent estimator are proposed to determine the optimal dimension number of a subspace, given the number of clusters.

Clustering for high-dimension, low-sample size data using distance vectors

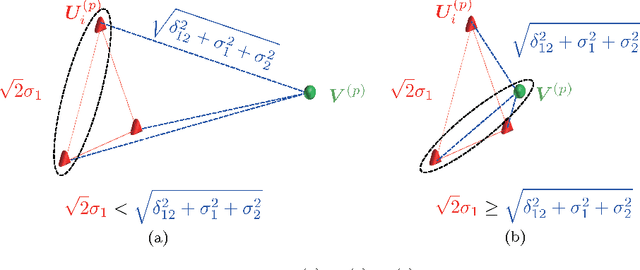
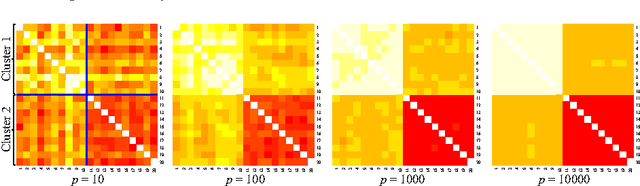
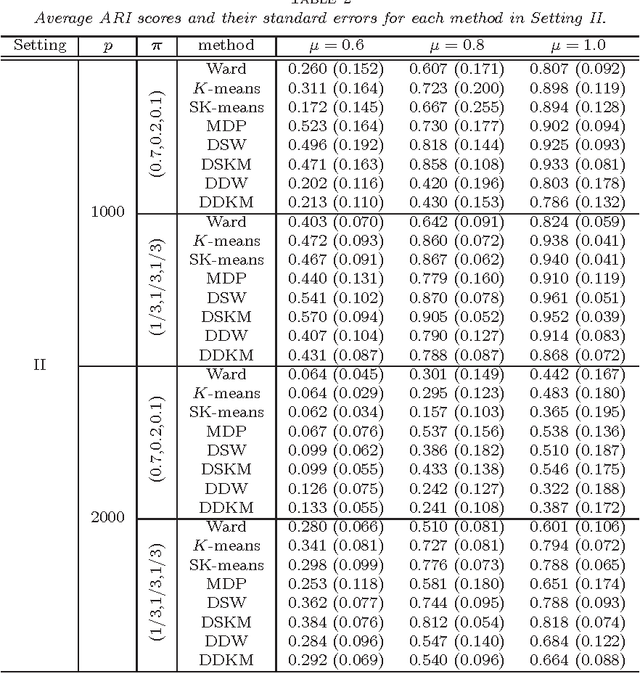
In high-dimension, low-sample size (HDLSS) data, it is not always true that closeness of two objects reflects a hidden cluster structure. We point out the important fact that it is not the closeness, but the "values" of distance that contain information of the cluster structure in high-dimensional space. Based on this fact, we propose an efficient and simple clustering approach, called distance vector clustering, for HDLSS data. Under the assumptions given in the work of Hall et al. (2005), we show the proposed approach provides a true cluster label under milder conditions when the dimension tends to infinity with the sample size fixed. The effectiveness of the distance vector clustering approach is illustrated through a numerical experiment and real data analysis.