George Wynne
Bayes Hilbert Spaces for Posterior Approximation
Apr 18, 2023Abstract:Performing inference in Bayesian models requires sampling algorithms to draw samples from the posterior. This becomes prohibitively expensive as the size of data sets increase. Constructing approximations to the posterior which are cheap to evaluate is a popular approach to circumvent this issue. This begs the question of what is an appropriate space to perform approximation of Bayesian posterior measures. This manuscript studies the application of Bayes Hilbert spaces to the posterior approximation problem. Bayes Hilbert spaces are studied in functional data analysis in the context where observed functions are probability density functions and their application to computational Bayesian problems is in its infancy. This manuscript shall outline Bayes Hilbert spaces and their connection to Bayesian computation, in particular novel connections between Bayes Hilbert spaces, Bayesian coreset algorithms and kernel-based distances.
A Spectral Representation of Kernel Stein Discrepancy with Application to Goodness-of-Fit Tests for Measures on Infinite Dimensional Hilbert Spaces
Jun 09, 2022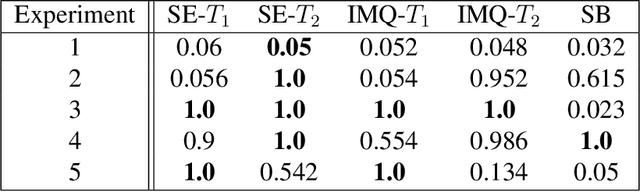
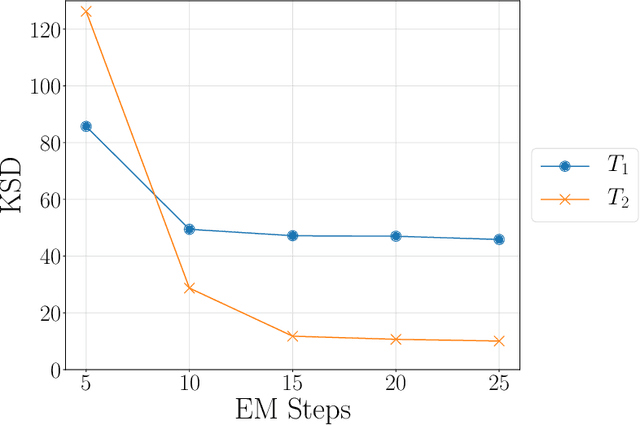

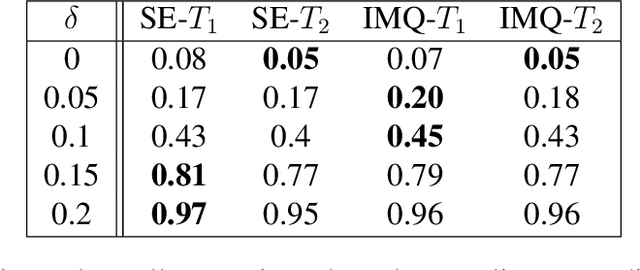
Abstract:Kernel Stein discrepancy (KSD) is a widely used kernel-based non-parametric measure of discrepancy between probability measures. It is often employed in the scenario where a user has a collection of samples from a candidate probability measure and wishes to compare them against a specified target probability measure. A useful property of KSD is that it may be calculated with samples from only the candidate measure and without knowledge of the normalising constant of the target measure. KSD has been employed in a range of settings including goodness-of-fit testing, parametric inference, MCMC output assessment and generative modelling. Two main issues with current KSD methodology are (i) the lack of applicability beyond the finite dimensional Euclidean setting and (ii) a lack of clarity on what influences KSD performance. This paper provides a novel spectral representation of KSD which remedies both of these, making KSD applicable to Hilbert-valued data and revealing the impact of kernel and Stein operator choice on the KSD. We demonstrate the efficacy of the proposed methodology by performing goodness-of-fit tests for various Gaussian and non-Gaussian functional models in a number of synthetic data experiments.
Grassmann Stein Variational Gradient Descent
Feb 07, 2022
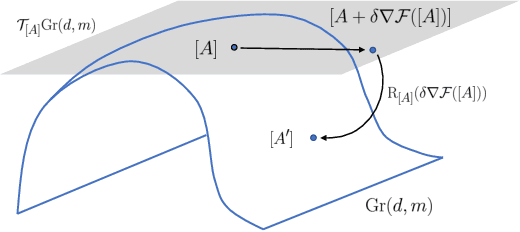
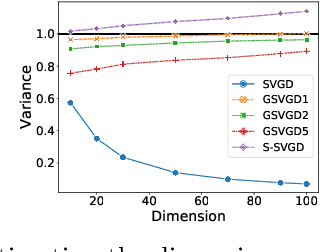
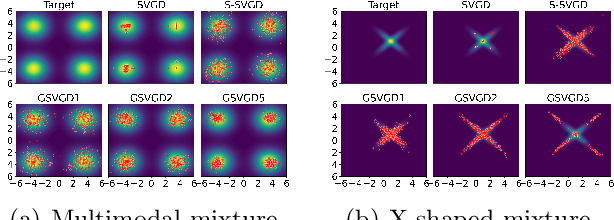
Abstract:Stein variational gradient descent (SVGD) is a deterministic particle inference algorithm that provides an efficient alternative to Markov chain Monte Carlo. However, SVGD has been found to suffer from variance underestimation when the dimensionality of the target distribution is high. Recent developments have advocated projecting both the score function and the data onto real lines to sidestep this issue, although this can severely overestimate the epistemic (model) uncertainty. In this work, we propose Grassmann Stein variational gradient descent (GSVGD) as an alternative approach, which permits projections onto arbitrary dimensional subspaces. Compared with other variants of SVGD that rely on dimensionality reduction, GSVGD updates the projectors simultaneously for the score function and the data, and the optimal projectors are determined through a coupled Grassmann-valued diffusion process which explores favourable subspaces. Both our theoretical and experimental results suggest that GSVGD enjoys efficient state-space exploration in high-dimensional problems that have an intrinsic low-dimensional structure.
Variational Gaussian Processes: A Functional Analysis View
Oct 25, 2021Abstract:Variational Gaussian process (GP) approximations have become a standard tool in fast GP inference. This technique requires a user to select variational features to increase efficiency. So far the common choices in the literature are disparate and lacking generality. We propose to view the GP as lying in a Banach space which then facilitates a unified perspective. This is used to understand the relationship between existing features and to draw a connection between kernel ridge regression and variational GP approximations.
Statistical Depth Meets Machine Learning: Kernel Mean Embeddings and Depth in Functional Data Analysis
May 26, 2021
Abstract:Statistical depth is the act of gauging how representative a point is compared to a reference probability measure. The depth allows introducing rankings and orderings to data living in multivariate, or function spaces. Though widely applied and with much experimental success, little theoretical progress has been made in analysing functional depths. This article highlights how the common $h$-depth and related statistical depths for functional data can be viewed as a kernel mean embedding, a technique used widely in statistical machine learning. This connection facilitates answers to open questions regarding statistical properties of functional depths, as well as it provides a link between the depth and empirical characteristic function based procedures for functional data.
A Kernel Two-Sample Test for Functional Data
Aug 25, 2020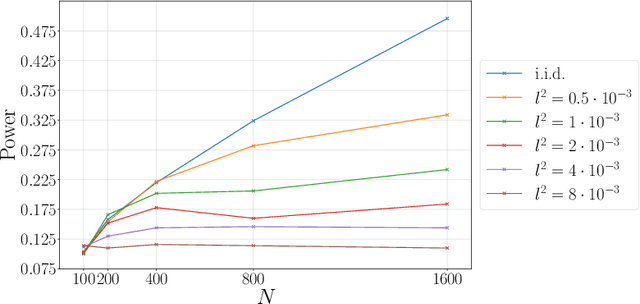
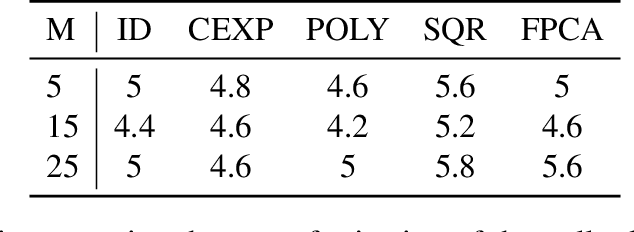
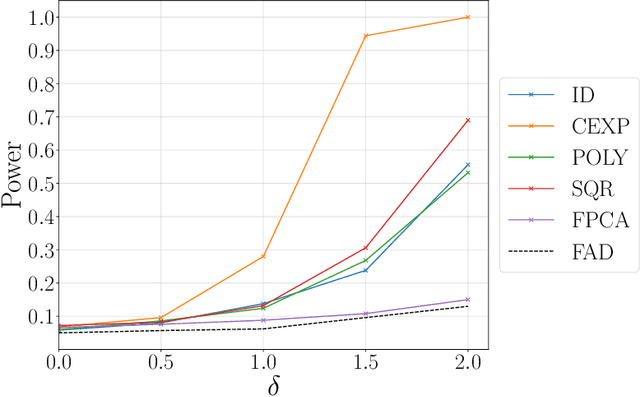
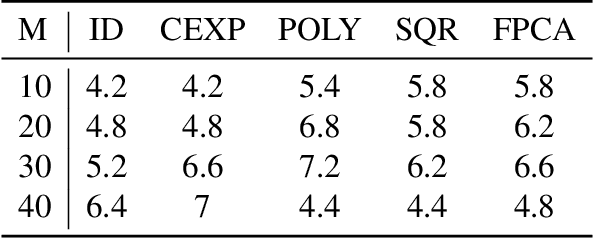
Abstract:We propose a nonparametric two-sample test procedure based on Maximum Mean Discrepancy (MMD) for testing the hypothesis that two samples of functions have the same underlying distribution, using a kernel defined on a function space. This construction is motivated by a scaling analysis of the efficiency of MMD-based tests for datasets of increasing dimension. Theoretical properties of kernels on function spaces and their associated MMD are established and employed to ascertain the efficacy of the newly proposed test, as well as to assess the effects of using functional reconstructions based on discretised function samples. The theoretical results are demonstrated over a range of synthetic and real world datasets.
Maximum likelihood estimation and uncertainty quantification for Gaussian process approximation of deterministic functions
Feb 24, 2020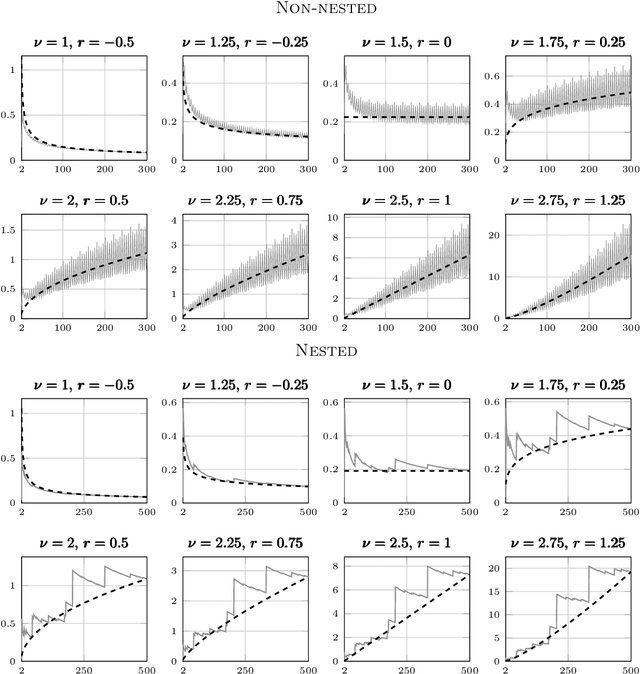
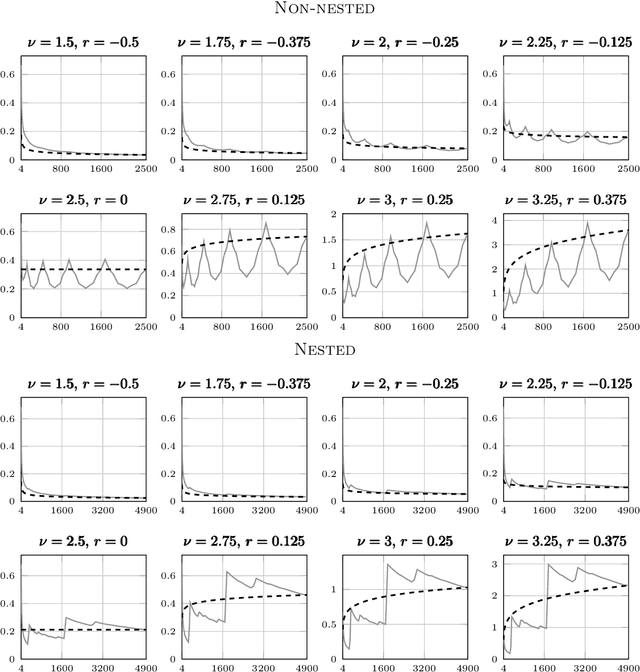
Abstract:Despite the ubiquity of the Gaussian process regression model, few theoretical results are available that account for the fact that parameters of the covariance kernel typically need to be estimated from the dataset. This article provides one of the first theoretical analyses in the context of Gaussian process regression with a noiseless dataset. Specifically, we consider the scenario where the scale parameter of a Sobolev kernel (such as a Mat\'ern kernel) is estimated by maximum likelihood. We show that the maximum likelihood estimation of the scale parameter alone provides significant adaptation against misspecification of the Gaussian process model in the sense that the model can become "slowly" overconfident at worst, regardless of the difference between the smoothness of the data-generating function and that expected by the model. The analysis is based on a combination of techniques from nonparametric regression and scattered data interpolation. Empirical results are provided in support of the theoretical findings.
Convergence Guarantees for Gaussian Process Approximations Under Several Observation Models
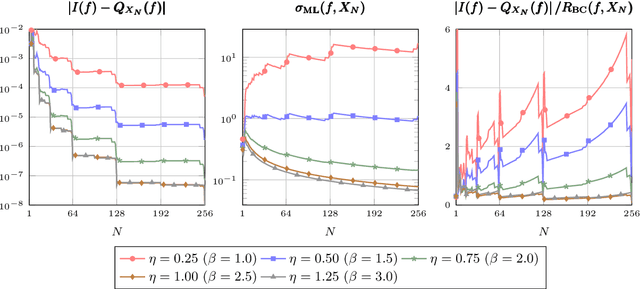
Jan 29, 2020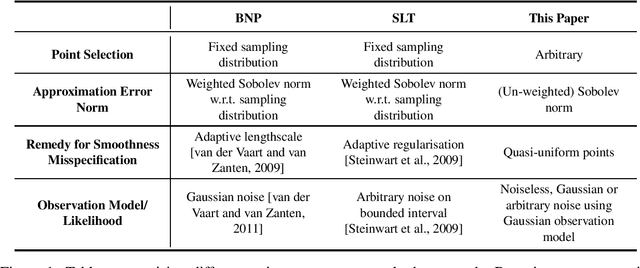
Abstract:Gaussian processes are ubiquitous in statistical analysis, machine learning and applied mathematics. They provide a flexible modelling framework for approximating functions, whilst simultaneously quantifying our uncertainty about this task in a computationally tractable manner. An important question is whether these approximations will be accurate, and if so how accurate, given our various modelling choices and the difficulty of the problem. This is of practical relevance, since the answer informs our choice of model and sampling distribution for a given application. Our paper provides novel approximation guarantees for Gaussian process models based on covariance functions with finite smoothness, such as the Mat\'ern and Wendland covariance functions. They are derived from a sampling inequality which facilitates a systematic approach to obtaining upper bounds on Sobolev norms in terms of properties of the design used to collect data. This approach allows us to refine some existing results which apply in the misspecified smoothness setting and which allow for adaptive selection of hyperparameters. However, the main novelty in this paper is that our results cover a wide range of observation models including interpolation, approximation with deterministic corruption and regression with Gaussian noise.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge