Configurable Multilingual ASR with Speech Summary Representations

Approximately half of the world's population is multilingual, making multilingual ASR (MASR) essential. Deploying multiple monolingual models is challenging when the ground-truth language is unknown in advance. This motivates research efforts on configurable multilingual MASR models that can be prompted manually or adapted automatically to recognise specific languages. In this paper, we present the Configurable MASR model with Summary Vector (csvMASR), a novel architecture designed to enhance configurability. Our approach leverages adapters and introduces speech summary vector representations, inspired by conversational summary representations in speech diarization, to combine outputs from language-specific components at the utterance level. We also incorporate an auxiliary language classification loss to enhance configurability. Using data from 7 languages in the Multilingual Librispeech (MLS) dataset, csvMASR outperforms existing MASR models and reduces the word error rate (WER) from 10.33\% to 9.95\% when compared with the baseline. Additionally, csvMASR demonstrates superior performance in language classification and prompting tasks.

Markovian Gaussian Process Variational Autoencoders

Deep generative models are widely used for modelling high-dimensional time series, such as video animations, audio and climate data. Sequential variational autoencoders have been successfully considered for many applications, with many variant models relying on discrete-time methods and recurrent neural networks (RNNs). On the other hand, continuous-time methods have recently gained attraction, especially in the context of irregularly-sampled time series, where they can better handle the data than discrete-time methods. One such class are Gaussian process variational autoencoders (GPVAEs), where the VAE prior is set as a Gaussian process (GPs), allowing inductive biases to be explicitly encoded via the kernel function and interpretability of the latent space. However, a major limitation of GPVAEs is that it inherits the same cubic computational cost as GPs. In this work, we leverage the equivalent discrete state space representation of Markovian GPs to enable a linear-time GP solver via Kalman filtering and smoothing. We show via corrupt and missing frames tasks that our method performs favourably, especially on the latter where it outperforms RNN-based models.

Convolutional Neural Processes for Inpainting Satellite Images

The widespread availability of satellite images has allowed researchers to model complex systems such as disease dynamics. However, many satellite images have missing values due to measurement defects, which render them unusable without data imputation. For example, the scanline corrector for the LANDSAT 7 satellite broke down in 2003, resulting in a loss of around 20\% of its data. Inpainting involves predicting what is missing based on the known pixels and is an old problem in image processing, classically based on PDEs or interpolation methods, but recent deep learning approaches have shown promise. However, many of these methods do not explicitly take into account the inherent spatiotemporal structure of satellite images. In this work, we cast satellite image inpainting as a natural meta-learning problem, and propose using convolutional neural processes (ConvNPs) where we frame each satellite image as its own task or 2D regression problem. We show ConvNPs can outperform classical methods and state-of-the-art deep learning inpainting models on a scanline inpainting problem for LANDSAT 7 satellite images, assessed on a variety of in and out-of-distribution images.

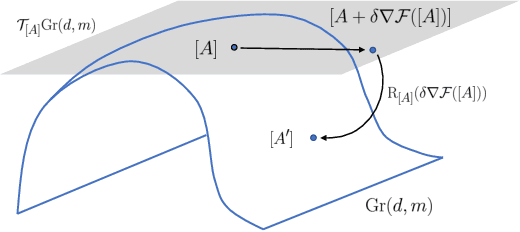
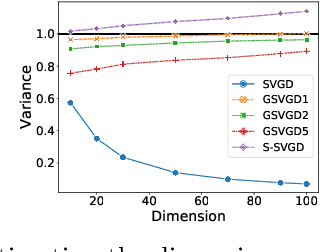
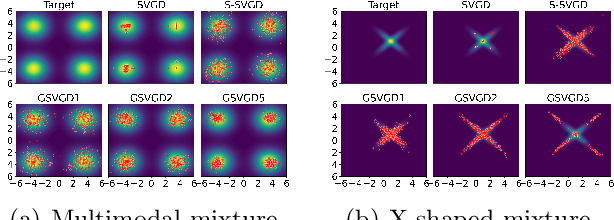
Grassmann Stein Variational Gradient Descent

Stein variational gradient descent (SVGD) is a deterministic particle inference algorithm that provides an efficient alternative to Markov chain Monte Carlo. However, SVGD has been found to suffer from variance underestimation when the dimensionality of the target distribution is high. Recent developments have advocated projecting both the score function and the data onto real lines to sidestep this issue, although this can severely overestimate the epistemic (model) uncertainty. In this work, we propose Grassmann Stein variational gradient descent (GSVGD) as an alternative approach, which permits projections onto arbitrary dimensional subspaces. Compared with other variants of SVGD that rely on dimensionality reduction, GSVGD updates the projectors simultaneously for the score function and the data, and the optimal projectors are determined through a coupled Grassmann-valued diffusion process which explores favourable subspaces. Both our theoretical and experimental results suggest that GSVGD enjoys efficient state-space exploration in high-dimensional problems that have an intrinsic low-dimensional structure.

Bayesian Probabilistic Numerical Integration with Tree-Based Models

Bayesian quadrature (BQ) is a method for solving numerical integration problems in a Bayesian manner, which allows user to quantify their uncertainty about the solution. The standard approach to BQ is based on Gaussian process (GP) approximation of the integrand. As a result, BQ approach is inherently limited to cases where GP approximations can be done in an efficient manner, thus often prohibiting high-dimensional or non-smooth target functions. This paper proposes to tackle this issue with a new Bayesian numerical integration algorithm based on Bayesian Additive Regression Trees (BART) priors, which we call BART-Int. BART priors are easy to tune and well-suited for discontinuous functions. We demonstrate that they also lend themselves naturally to a sequential design setting and that explicit convergence rates can be obtained in a variety of settings. The advantages and disadvantages of this new methodology are highlighted on a set of benchmark tests including the Genz functions, and on a Bayesian survey design problem.